本文主要是介绍python数据分析案例-信用卡违约预测分析,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、研究背景和意义
信用卡已经成为现代社会中人们日常生活中不可或缺的支付工具,它不仅为消费者提供了便利,还为商家提供了更广泛的销售渠道。然而,随着信用卡的普及和使用量的增加,信用卡违约问题逐渐成为金融机构面临的重要挑战。信用卡违约不仅给金融机构带来财务损失,还损害了其声誉和信用评级,从而影响其长期可持续发展。因此,有效预测信用卡违约风险对金融机构来说至关重要。。。。。
二、实证分析
这个数据集包含了2005年4月至2005年9月期间台湾信用卡客户的违约支付、人口统计因素、信用数据、支付历史和账单明细的信息。数据集中有25个变量:
ID:每个客户的ID
LIMIT_BAL:给定信用额度(新台币,包含个人和家庭/附属信用额度)
-SEX:性别(1=男性,2=女性)
-EDUCATION:教育程度(1=研究生,2=大学,3=高中,4=其他,5=未知,6=未知)
MARRIAGE**:婚姻状况(1=已婚,2=单身,3=其他)
AGE**:年龄(岁)
PAY_0:2005年9月的还款状态(-1=按时支付,1=延迟一个月,2=延迟两个月,…,8=延迟八个月,9=延迟九个月及以上)
PAY_2:2005年8月的还款状态(同上)
PAY_3:2005年7月的还款状态(同上)
PAY_4:2005年6月的还款状态(同上)
PAY_5:2005年5月的还款状态(同上)
PAY_6:2005年4月的还款状态(同上)
BILL_AMT1:2005年9月的账单金额(新台币)
BILL_AMT2:2005年8月的账单金额(新台币)
BILL_AMT3:2005年7月的账单金额(新台币)
BILL_AMT4:2005年6月的账单金额(新台币)
BILL_AMT5:2005年5月的账单金额(新台币)
BILL_AMT6:2005年4月的账单金额(新台币)
PAY_AMT1:2005年9月的上期还款金额(新台币)
PAY_AMT2:2005年8月的上期还款金额(新台币)
PAY_AMT3:2005年7月的上期还款金额(新台币)
PAY_AMT4:2005年6月的上期还款金额(新台币)
PAY_AMT5:2005年5月的上期还款金额(新台币)
PAY_AMT6:2005年4月的上期还款金额(新台币)
default.payment.next.month:下个月是否违约(1=是,0=否)
首先导入数据分析的包:
from mpl_toolkits.mplot3d import Axes3D
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt # plotting
import numpy as np # linear algebra
import os # accessing directory structure
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression, RidgeClassifier
from sklearn.metrics import accuracy_score,classification_report,confusion_matrix,mean_squared_error
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline读取数据并且查看前五行
df1 = pd.read_csv('UCI_Credit_Card.csv', delimiter=',')
df1.dataframeName = 'UCI_Credit_Card.csv'
nRow, nCol = df1.shape
print(f'There are {nRow} rows and {nCol} columns')
对数据集特征进行了描述性统计分析:
数据和代码
报告代码数据
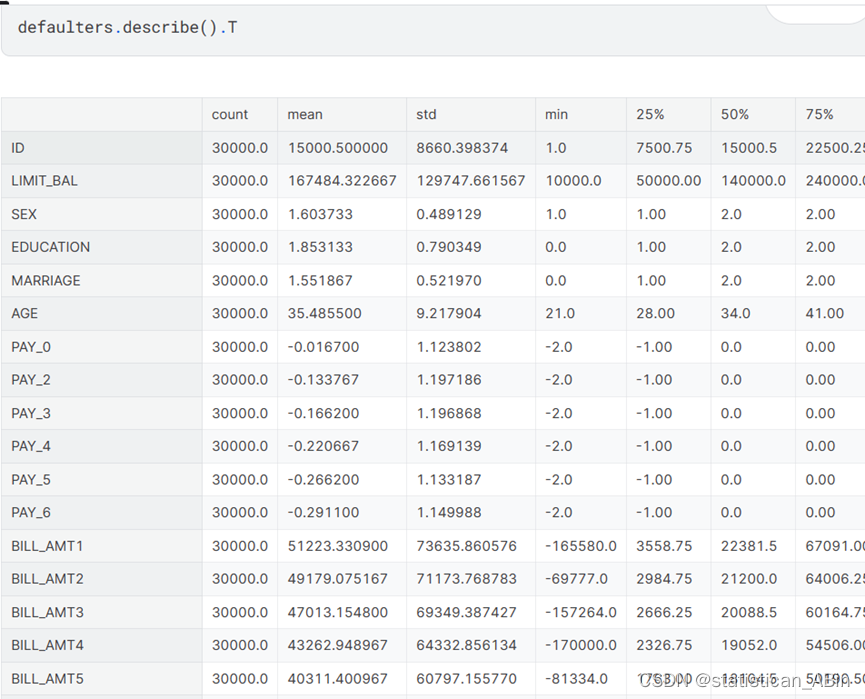
这些数据描述了一位信用卡用户和历史信用卡使用情况。总体来说: 用户的ID分布在1到30,000之间,平均值为15,000.5,标准差为8,660.4。信用额度(LIMIT_BAL)的平均值为167484.32,标准差为129747.66,范围从10,000到1,000,000。性别(SEX)的平均值约为1.60,这可能表示1是男性,2是女性。教育程度(EDUCATION)的平均值约为1.85,可能被分类为0到6之间的不同等级。。。。。
接下来查看数据类型:

我们看到所有列都是int64类型,而根据之前的知识,我们知道SEX、EDUCATION、MARRIAGE、PAY_0、PAY_2、PAY_3、PAY_4、PAY_5、PAY_6、default_payment_next_month是分类特征。所以我们将这些特征转换为分类类型。接下来,检查缺失值。 从以上结果可以注意到没有缺失值。
defaulters.isna().sum() # check for missing values for surity
接下来是可视化部分,在进入可视化之前,我们首先选择一些我们认为与目标变量最相关的特征。
def_cnt = (defaulters.def_pay.value_counts(normalize=True)*100)
def_cnt.plot.bar(figsize=(6,6))
plt.xticks(fontsize=12, rotation=0)
plt.yticks(fontsize=12)
plt.title("Probability Of Defaulting Payment Next Month", fontsize=15)
for x,y in zip([0,1],def_cnt):plt.text(x,y,y,fontsize=12)
plt.show()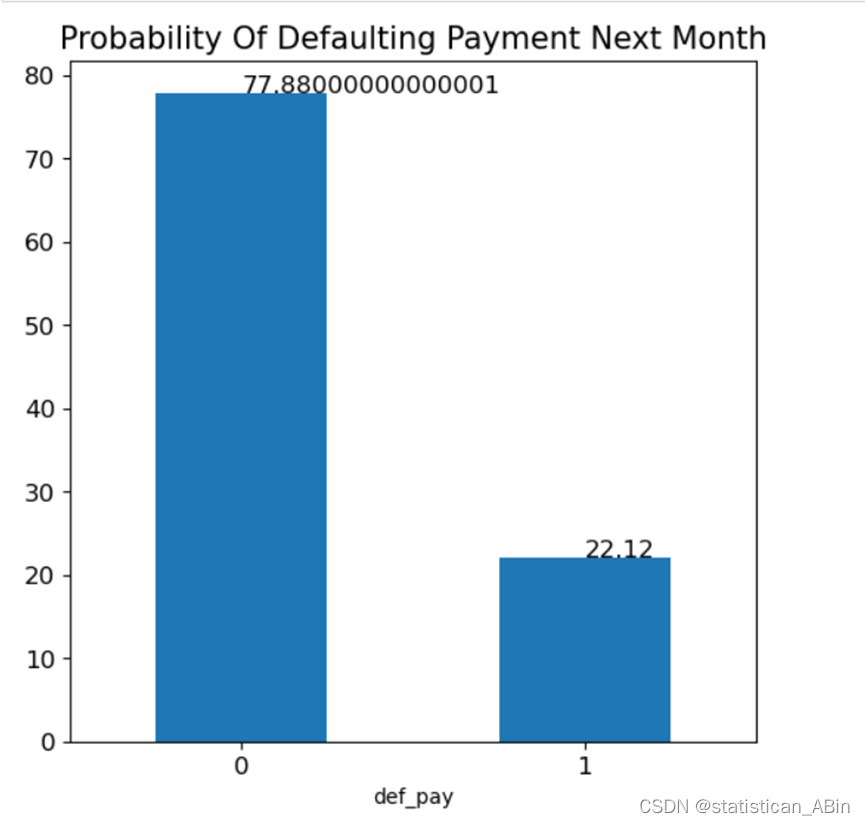
我们可以看到数据集中的77.8%客户预计不会违约,而22.3%客户预计会违约。 接下来绘制年龄变量的可视化并继续探索。

通过绘制连续变量的图表,我们观察到数据集包含了倾斜的信用额度和客户年龄数据。我们有更多信用额度在0到200000货币之间的客户。我们有更多20到40岁年龄段的客户,即主要是年轻到中年群体。我们将在下面观察变量对目标变量的影响。
接下来我们将年龄分组,以探索年龄和支付逾期之间的关系:
bins = [20,30,40,50,60,70,80]
names = ['21-30','31-40','41-50','51-60','61-70','71-80']
defaulters['AGE_BIN'] = pd.cut(x=defaulters.AGE, bins=bins, labels=names, right=True)age_cnt = defaulters.AGE_BIN.value_counts()
age_0 = (defaulters.AGE_BIN[defaulters['def_pay'] == 0].value_counts())
age_1 = (defaulters.AGE_BIN[defaulters['def_pay'] == 1].value_counts())plt.subplots(figsize=(8,5))
# sns.barplot(data=defaulters, x='AGE_BIN', y='LIMIT_BAL', hue='def_pay', ci=0)
plt.bar(age_0.index, age_0.values, label='0')
plt.bar(age_1.index, age_1.values, label='1')
for x,y in zip(names,age_0):plt.text(x,y,y,fontsize=12)
for x,y in zip(names,age_1):plt.text(x,y,y,fontsize=12)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
plt.title("Number of clients in each age group", fontsize=15)
plt.legend(loc='upper right', fontsize=15)
plt.show()
我们的客户主要集中在21-30岁年龄段,其次是31-40岁。因此,随着年龄组的增加,下个月将违约的客户数量正在减少。。。。检查下个月逾期还款的客户百分比:
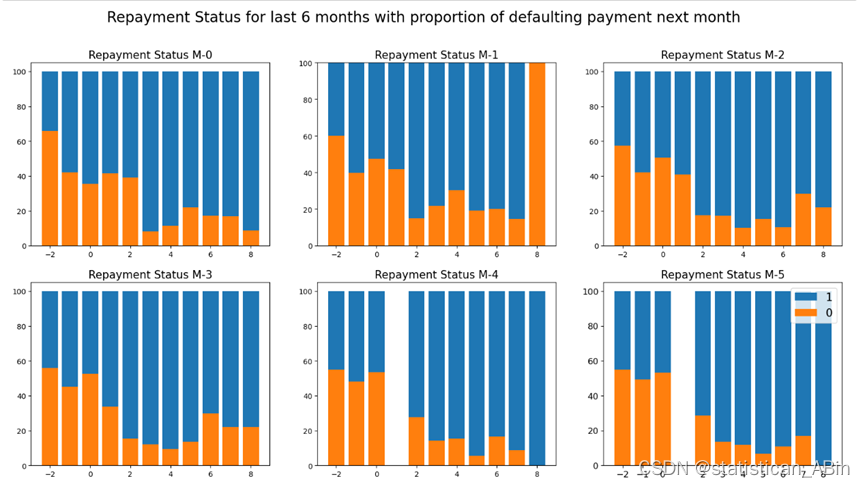
从图中可以看到,对于当前月份状态,还款越早,这些客户违约的可能性越小。 接下来探索婚姻状况是否对信用卡逾期还款有影响:
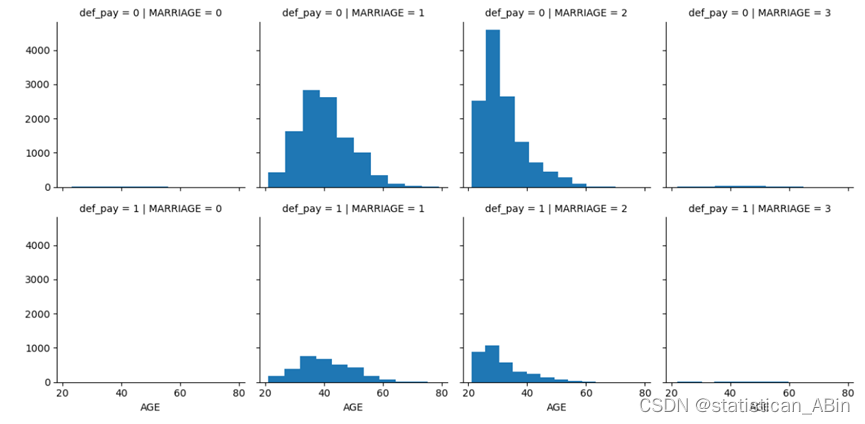
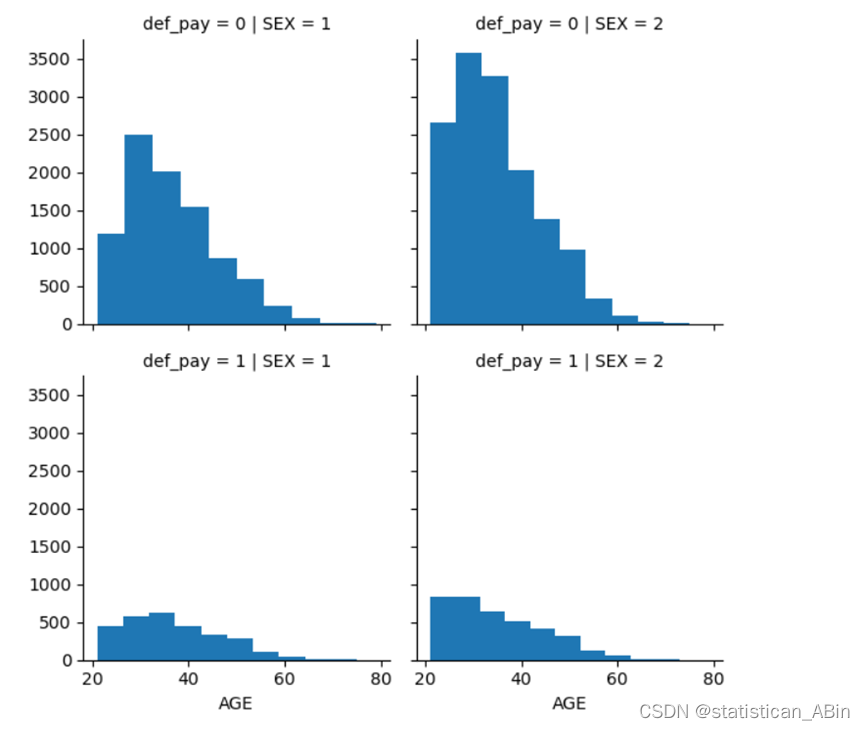
可以看到,20-30岁年龄段的女性比所有年龄段的男性更容易违约。因此我们可以保留客户的性别列来预测违约的概率。 现在我们将检查过去六个月的账单金额是否会影响下个月的违约情况:
plt.subplots(figsize=(20,10))plt.subplot(231)
plt.scatter(x=defaulters.PAY_AMT1, y=defaulters.BILL_AMT1, c='r', s=1)plt.subplot(232)
plt.scatter(x=defaulters.PAY_AMT2, y=defaulters.BILL_AMT2, c='b', s=1)plt.subplot(233)
plt.scatter(x=defaulters.PAY_AMT3, y=defaulters.BILL_AMT3, c='g', s=1)plt.subplot(234)
plt.scatter(x=defaulters.PAY_AMT4, y=defaulters.BILL_AMT4, c='c', s=1)
plt.ylabel("Bill Amount in past 6 months", fontsize=25)plt.subplot(235)
plt.scatter(x=defaulters.PAY_AMT5, y=defaulters.BILL_AMT5, c='y', s=1)
plt.xlabel("Payment in past 6 months", fontsize=25)plt.subplot(236)
plt.scatter(x=defaulters.PAY_AMT6, y=defaulters.BILL_AMT6, c='m', s=1)plt.show()

上图显示,对于账单金额较高但支付金额很低的客户比例较高。
使用groupby()函数计算不同教育水平的人的数量:
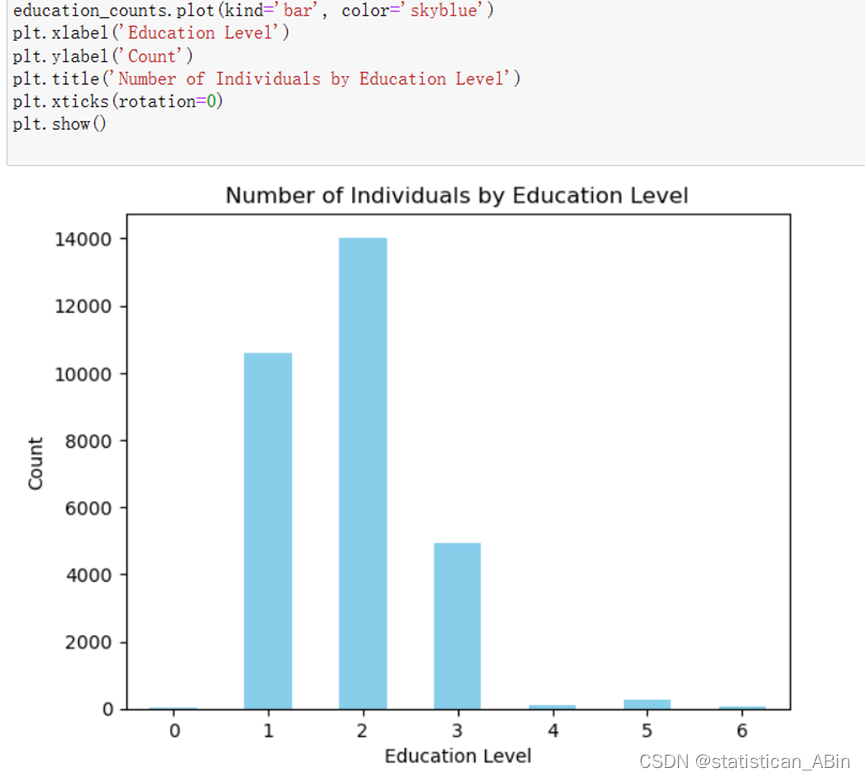
接下来进行了模型预测,这里选择的模型是LogisticRegression和RidgeClassifier模型。 接下来按8:2的比例划分训练集和测试集。
X_train, X_test, y_train, y_test = train_test_split(df_X, df_y, test_size=0.2, random_state=10)
model1 = LogisticRegression()
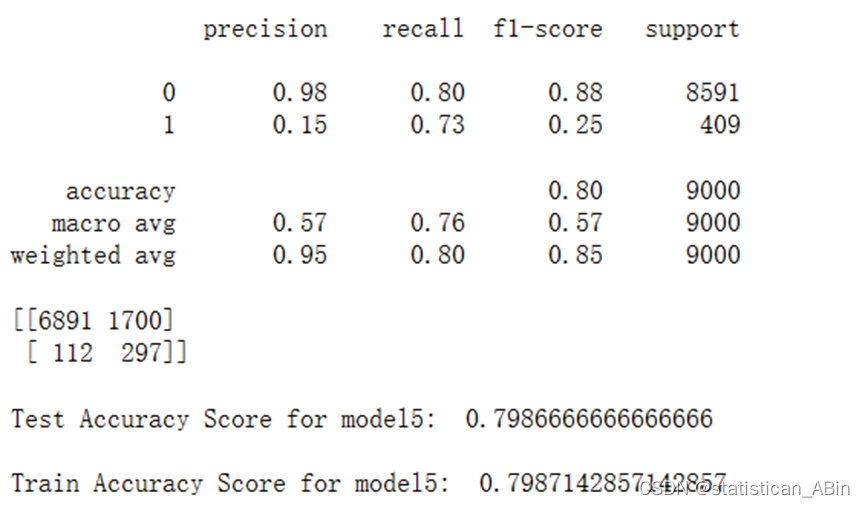
model1.fit(X_train, y_train)y_pred = model1.predict(X_test)print(classification_report(y_pred, y_test))
print(confusion_matrix(y_pred, y_test))
print('\nAccuracy Score for model1: ', accuracy_score(y_pred,y_test))
cm_model1 = [[4681, 1317],[2, 0]]
plt.figure(figsize=(8, 6))
sns.heatmap(cm_model1, annot=True, cmap='Blues', fmt='g', xticklabels=['Predicted 0', 'Predicted 1'], yticklabels=['Actual 0', 'Actual 1'])
plt.title('Confusion Matrix - Model 1')
plt.xlabel('Predicted Labels')
plt.ylabel('True Labels')
plt.show()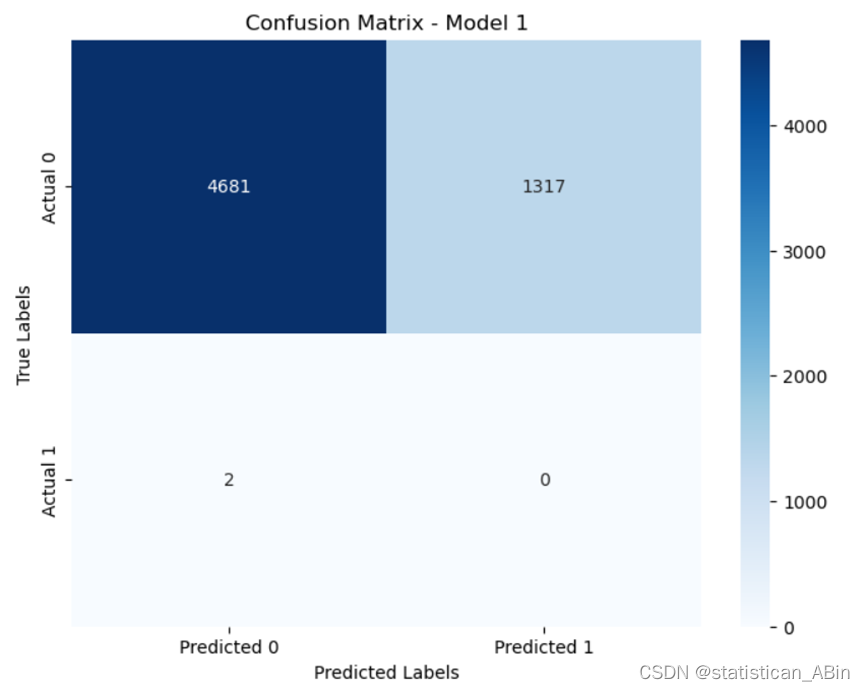
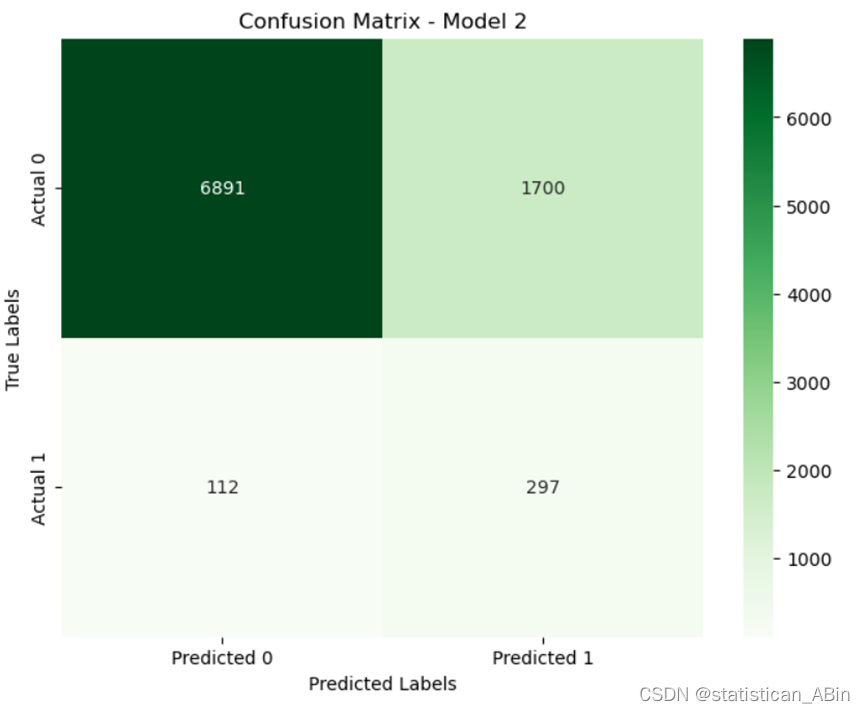
这两个模型的结果显示了一些有趣的现象。首先,我们可以看到第一个模型在类别0(未违约)上的准确率(精度)为100%,但在类别1(违约)上的准确率为0%。这表明该模型在预测违约客户时存在严重问题,可能存在严重偏差或无法识别任何违约客户。。。。。
三、结论
本研究通过对台湾信用卡客户数据集的分析,构建了信用卡违约预测模型。研究结果表明,年龄、婚姻状况、性别、教育程度、还款历史和账单金额等因素对信用卡违约有显著影响。在模型选择方面,LogisticRegression 和 RidgeClassifier 模型在预测信用卡违约方面都有一定的表现。。。。。
参考文献
[1] Tian Yuan,Guo Honglie,Ji Qian. Credit card risky customer prediction based on SMOTEENN-XGBoost[J/OL].SoftwareGuide.
[2] LU Rongwei, HUANG Chang'e, XIE Jiuhui. Research on credit card overdue prediction based on machine learning[J]. Science and Technology Innovation,2024,(06):130-133.
创作不易,希望大家多点赞关注评论!!!(类似代码或报告定制可以私信)
这篇关于python数据分析案例-信用卡违约预测分析的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





