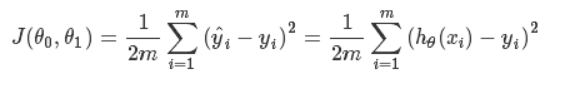本文主要是介绍吴恩达机器学习笔记(week1——week5),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Week1
转自该大神~~~~~ http://scruel.gitee.io/ml-andrewng-notes/week1.html
一、 引言(Introduction)
1.1 欢迎
1.2 机器学习是什么?
1.3 监督学习
1.4 无监督学习
二、单变量线性回归(Linear Regression with One Variable)
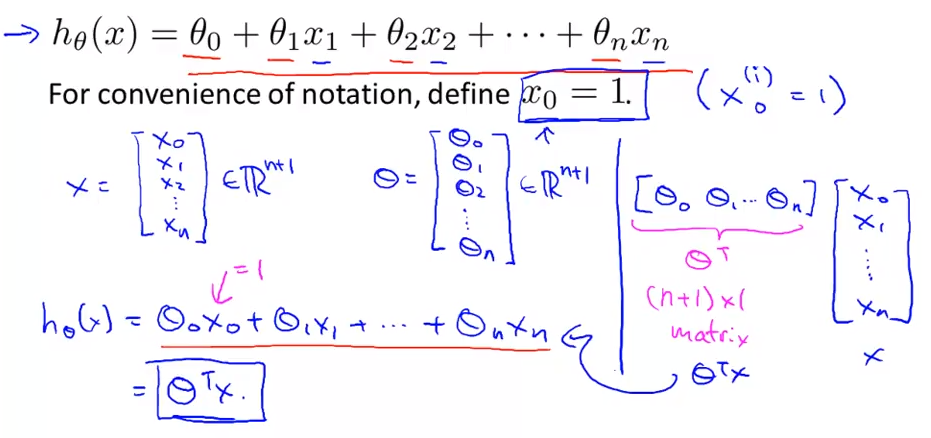
2.1 模型表示
2.2 代价函数
2.3 代价函数的直观理解I
2.4 代价函数的直观理解II
2.5 梯度下降
2.6 梯度下降的直观理解
2.7 梯度下降的线性回归
2.8 接下来的内容
三、线性代数回顾(Linear Algebra Review)
3.1 矩阵和向量
3.2 加法和标量乘法
3.3 矩阵向量乘法
3.4 矩阵乘法
3.5 矩阵乘法的性质
3.6 逆、转置
补充:
A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E
一个程序被认为能从经验E中学习解决任务 T,达到 性能度量值P,当且仅当,有了经验E后,经过P评判, 程序在处理 T 时的性能有所提升。
一般来说,任何机器学习问题都可以分配到两大类中的一个:有监督学习和无监督学习。
监督学习
在监督式学习中,我们得到了一个数据集,并且已经知道我们的正确输出应该是什么样子,并且认为输入和输出之间存在关系。监督学习问题分为“回归”和“分类”问题。在回归问题中,我们试图预测连续输出中的结果,这意味着我们试图将输入变量映射到某个连续函数。在分类问题中,我们试图预测离散输出中的结果。换句话说,我们试图将输入变量映射到离散的类别中。
例1:
给定有关房地产市场上房屋大小的数据,尝试预测其价格。作为尺寸函数的价格是连续的输出,所以这是一个回归问题。我们可以把这个例子变成一个分类问题,而不是让我们的输出关于房子是“卖出多少还是低于要价”。在这里,我们将基于价格的房屋分为两类。
例2:
(a)回归 - 给定一张人的照片,我们必须根据给定的图片预测他们的年龄
(b)分类 - 给予患有肿瘤的患者,我们必须预测肿瘤是恶性的还是良性的。
无监督学习
无监督学习使我们能够很少或根本不知道我们的结果应该是什么样子。 我们可以从数据中得出结构,我们不一定知道变量的影响。我们可以通过基于数据中变量之间的关系对数据进行聚类来推导出这种结构。
在无监督学习的情况下,没有基于预测结果的反馈。
例:
聚类:获取1,000,000个不同基因的集合,并找到一种方法将这些基因自动分组成不同变量的相似或相关的组,例如寿命,位置,角色等。
非聚类:“鸡尾酒会算法”,允许您在混乱的环境中查找结构。 (即在鸡尾酒会上识别来自声音网格的个人声音和音乐)。
代价函数
通过使用代价函数来衡量假设函数的准确性。该函数被称为“平方误差函数”或“均方误差”。
以下图片总结了代价函数的作用:
Week2
大神笔记 http://scruel.gitee.io/ml-andrewng-notes/week2.html
四、多变量线性回归(Linear Regression with Multiple Variables)
4.1 多维特征
4.2 多变量梯度下降
4.3 梯度下降法实践1-特征缩放
4.4 梯度下降法实践2-学习率
4.5 特征和多项式回归
4.6 正规方程
4.7 正规方程及不可逆性(选修)
五、Octave教程(Octave Tutorial)
5.1 基本操作
5.2 移动数据
5.3 计算数据
5.4 绘图数据
5.5 控制语句:for,while,if语句
5.6 向量化 88
5.7 工作和提交的编程练习
补充:
以下为便于理解添加的图或内容
4.1多特征:
4.2多变量梯度下降
一与多:
4.3梯度下降——特征值缩放
4.4梯度下降——学习效率
4.5特征和多项式回归
我们可以通过使它成为二次函数,立方函数或平方根函数(或任何其他形式)来改变我们的假设函数的行为或曲线。线性回归只能以直线来对数据进行拟合,有时候需要使用曲线来对数据进行拟合,即多项式回归(Polynomial Regression)。在使用多项式回归时,要记住非常有必要进行特征缩放,比如 的范围为 1-1000,那么 的范围则为 1- 1000000,不适用特征缩放的话,范围更有不一致,也更易影响效率。
4.6正规方程(标准化方程):
矩阵的求导公式是关键,图片转载自https://blog.csdn.net/perfect_accepted/article/details/78383434
4.7不可逆性正规方程
选讲
Week3
大神笔记http://scruel.gitee.io/ml-andrewng-notes/week3.html#header-n109
六、逻辑回归(Logistic Regression)
6.1 分类问题
6.2 假说表示
6.3 判定边界
6.4 代价函数
6.5 简化的成本函数和梯度下降
6.6 高级优化
6.7 多类别分类:一对多
七、正则化(Regularization)
7.1 过拟合的问题
7.2 代价函数
7.3 正则化线性回归
7.4 正则化的逻辑回归模型
补充:
6.5 简化的成本函数和梯度下降(Simplified Cost Function and Gradient Descent)
此 逻辑回归中代价函数求导推导 更容易理解
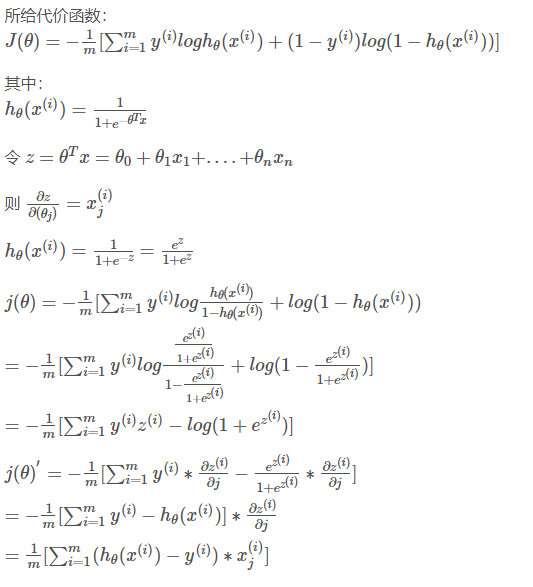
7.2 代价函数(Cost Function)
调整学习速率和正则化参数的技巧:
先调整学习速率,使迭代次数在一个可以接受的范围内,因此学习速率过小,会导致迭代次数很大,初始lambda是不是应该设为0。
1.在现有学习速率的基础上,在验证集上调整正则化参数,主在是判断是不是出现了variant和bias的问题。
(1)如果lambda过小,则可能会出现variant问题,那就是训练误差很小,而验证集上的误差很大,增加labmda会使步长(学习速率与增量的乘积)变小,学习速率变慢。(2)如果lambda过大,则可能会出现bias的问题,就是训练误差和验证误差都很大,并且相差很小,减少lambda会使步长变大,从而使得收敛速度变快。
2.最终的结果应该是使得训练误差和验证误差都比较小,而且很接近,并且训练误差在有限迭代次数内能达到最小值。(1)增加学习速率,相当于增加步长,也相当于增加正则化参数
(2)减小学习速率,相当于减小步长,也相当于减小正则化参数。
3. 在现有基础上,由于增加lambda会使学习速率变慢,因此需要在轻度过拟合的时候增加学习速率的值,这样也可以进一步减轻过拟合问题(增加学习速率,会变相增加正则化参数)。也就是当存在轻度过拟合问题,并且学习过程过慢的情况下,应该增加学习速率的值,而不是正则化参数lambda的值。但是如果学习速率过大,会导致步长过大,导致训练误差比较大,进一步也会影响验证误差,也就是说增加学习速率会有可能会使验证误差变大。
4. 如果lambda过大,则会出现bias的问题,这时应该减少lambda的值,注意,这也相当于减小了步长,会使收敛速率加快。需要注意的是:验证集上的误差会在迭代过程中,出现先小后大的情况,我们似乎只需要关注在训练集上收敛的情况。
由于限制了迭代的次数,所以在准确率上会有所损失(训练误差只是近似最优),但应该也在可以接受的范围之内。在过拟合情况下,训练误差的最优值会比较小,而在正常情况下,训练误差会比较大,也验证误差相当。因此,在调参的过程中,会出现训练误差逐步增加的情况(从过学习到正常情况)。
Week4
大神笔记: http://ai-start.com/ml2014/html/week4.html#header-n634
第八、神经网络:表述(Neural Networks: Representation)
8.1 非线性假设
8.2 神经元和大脑
8.3 模型表示1
8.4 模型表示2
8.5 样本和直观理解1
8.6 样本和直观理解II
8.7 多类分类
补充:8.7 Suppose you have a multi-class classification problem with 10 classes. Your neural network has 3 layers, and the hidden layer (layer 2) has 5 units. Using the one-vs-all method described here, how many elements does Θ(2)
50 55 60√ 66
多类分类器包含十个类,第三层激活单元为10作θ行,第二层有5个单元,加上一个偏差,则为6个作θ列,θ维度应为10*6
异或实现XOR (x1 OR x2) AND ((NOT x1) OR (NOT x2))
Week5
http://scruel.gitee.io/ml-andrewng-notes/week5.html
http://ai-start.com/ml2014/html/week5.html
任何布尔函数都可由两层神经网络准确表达,但所需的中间单元的数量随输入呈指数级增长;
任何连续函数都可由两层神经网络以任意精度逼近;
任何函数都可由三层神经网络以任意程度逼近。
九、神经网络的学习(Neural Networks: Learning)
9.1 代价函数
9.2 反向传播算法
9.3 反向传播算法的直观理解
9.4 实现注意:展开参数
9.5 梯度检验
9.6 随机初始化
9.7 综合起来
9.8 自主驾驶
这篇关于吴恩达机器学习笔记(week1——week5)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!