本文主要是介绍模式分解的概念(下)-无损连接分解的与保持函数依赖分解的定义和判断、损失分解,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、无损连接分解
1、定义

2、检验一个分解是否是无损连接分解的算法
输入与输出
输入:
关系模式R(U,F),F是最小函数依赖集
R上的一个分解
输出:
判断分解是否为无损连接分解

(1)建立一张k行n列的表,每行对应分解中的一个关系模式,每列对应一个属性
,若属性
,则在i行j列处填
,否则填
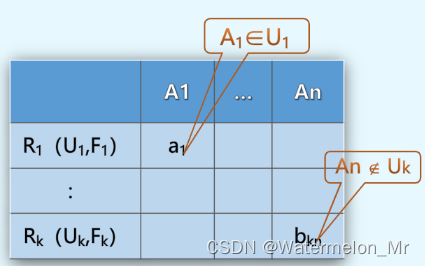
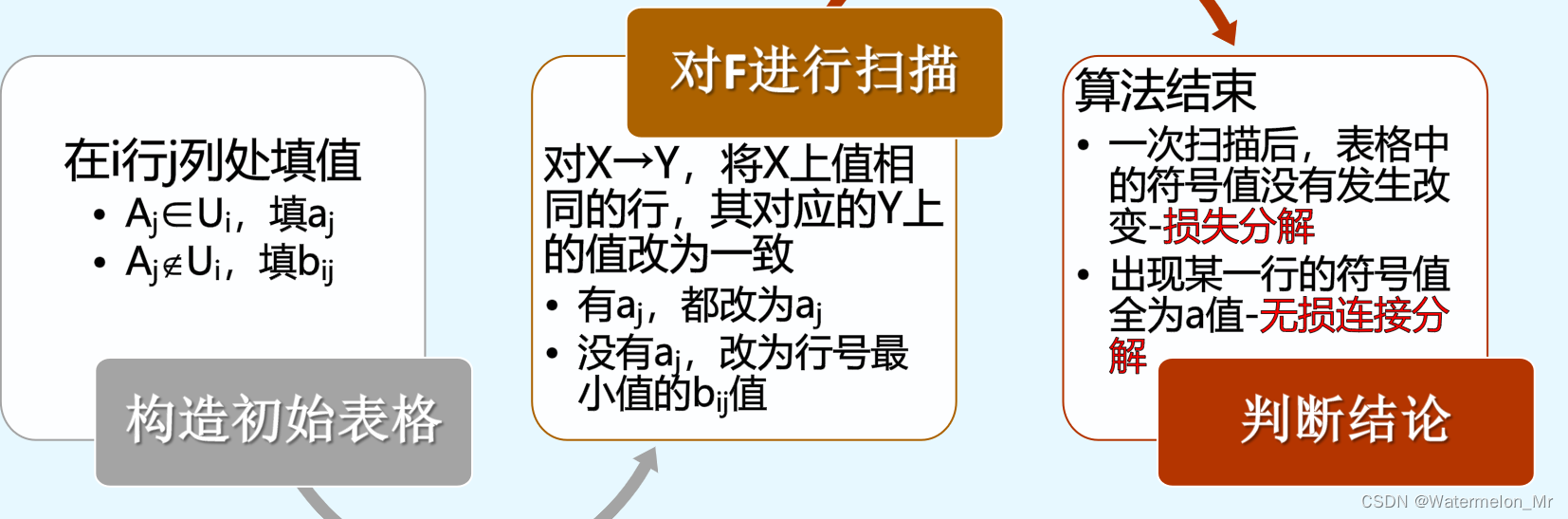
(2)对形如的函数依赖,检查X属性列上值相同的行,其所对应的Y属性列上的值是否相
同。若Y属性列上的值不相同,则将Y属性列上的符号值改为一致。修改符号值的规则为对应行中1
的Y属性列中如果存在,则都改为
,否则都改为
。整个第(2)步被称为对F的一次扫描
(3)一次扫描后,判断表格中的符号值是否发生改变,如果发生改变,则执行(2),否则算法结
束,特殊的,当表格中的出现某一行的符号值全为a值时算法也结束
定理:为无损连接的充分必要条件是算法终止时,表中有一行为
。
使用定理对表格进行判断,即可得出改分解是无损连接分解还是损失分解
二、无损连接分解的判定定理

举例:无损分解

举例:损失分解

三、保持函数依赖分解
1、定义
 2、判断分解
2、判断分解是否保存函数依赖的方法

如果均属于,则分解保存函数依赖,是函数依赖分解
3、举例:

四、小结
1、模式分解的两个特性涉及到了两个数据库模式的等价问题,这种等价包括数据等价和语义等价两个方面, 数据等价是指两个数据库实例表示同样的信息内容,用无损连接分解来衡量,语义等价是指两个数据库模式具有相同函数依赖集闭包,数据语义没有丢失,用保持函数依赖来衡量
2、无损连接性与保持函数依赖之间没有必然的联系
这篇关于模式分解的概念(下)-无损连接分解的与保持函数依赖分解的定义和判断、损失分解的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






