本文主要是介绍DS:堆的应用——两种算法和TOP-K问题,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
欢迎来到Harper.Lee的学习世界!
博主主页传送门:Harper.Lee的博客主页
想要一起进步的uu可以来后台找我哦!
一、堆的排序
1.1 向上调整——建小堆
1.1.1 代码实现
//时间复杂度:O(N*logN)
//空间复杂度:O(logN)
for (int i = 1; i < n; i++)
{AdjustUp(a, i);
}1.1.2 复杂度分析
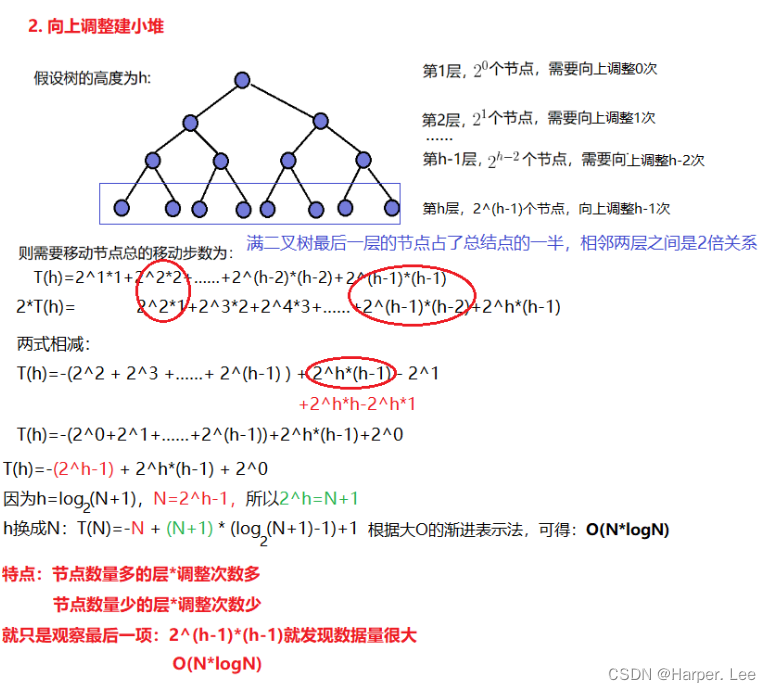
1.1.3 深入讨论
Q1:向上调整建堆的开始位置是哪里?
A:向上调整需要从最后一层的节点开始向上调整。
Q2:排好最后一层数据,时间消耗为多少?
A:向上调整建堆过程中,最后一层占了至少一半的节点,最多向上调整 N/2*(logN-1) 次,基本上就接近了O(N*logN)了。(tips:相邻两层之间的节点是2倍关系,50%、25%、12.5%……)
1.2 向下调整——建大堆
1.2.1 代码实现
//时间复杂度:O(N)
//空间复杂度:O(logN)
for (int i = (n-1-1)/2; i >= 0; i--)
{AdjustDown(a, n, i);//n代表数据个数
}1.2.2 复杂度分析

1.2.3 深入讨论
Q1:向下调整建堆最开始调整的位置是哪里?
A:从最后一个非叶子节点开始调整,而不是第一层开始调整。
Q2:为什么向上调整和向下调整都不传入堆数据结构作为参数呢?
A:为了方便对向上调整算法和 向下调整算法进行更方便的使用。
1.3 堆排序的实现
1.3.1 小根堆排降序
//降序 建小堆 向上调整O(N*logN)
void Decreasing_HeapSort(int* a, int n)
{//for (int i = 1; i < n; i++){AdjustUp(a, i);}//循环次数是N,但是向下调整的次数是变化的,时间复杂度:O(N*logN) int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0); --end;}
}1.3.2 大根堆排升序
//升序 建大堆 向下调整O(N)
void Rising_HeapSort(int* a, int n)
{for (int i = (n-1-1)/2; i >=0;i--)AdjustDown(a, n, i);//开始排序 先交换向下调整//循环次数是N,但是向下调整的次数是变化的,时间复杂度:O(N*logN) int end = n - 1;while (end >= 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);--end;}
}1.4 冒泡排序vs堆排序
| 排序方式 | 时间复杂度 | 实际作用 |
| 堆排序 | O(n*logn) | 实践意义 |
| 冒泡排序 | O(n^2) | 教学意义 |
运用clock函数可以测试冒泡排序和堆排序运行所用的时间。
二、补充-增容(顺序栈的内容)
2.1 代码实现
//增容函数
void SLCheckCapacity(SL* ps)
{//插入数据之前先看空间够不够if (ps->capacity == ps->size){//申请空间//malloc calloc realloc int arr[100] --->增容realloc//三目表达式int newCapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;SLDataType* tmp = (SLDataType*)realloc(ps->arr, newCapacity * sizeof(SLDataType));//要申请多大的空间if (tmp == NULL){perror("realloc fail!");exit(1);//直接退出程序,不再继续执行}//空间申请成功ps->arr = tmp;ps->capacity = newCapacity;}
}2.2 深入讨论
1. 增容使用哪个函数?
使用realloc,因为它有增容的概念,而且可以进行多次增容;malloc和calloc都可以用来申请一段连续的空间,但是它们都没有增容的概念。
值得注意的是:(1)realloc增容的第二个参数单位是字节,所以代码中的newCapacity需要乘以sizeof(SLDataType);(2)使用realloc申请空间可能会申请失败,realloc返回 EOF,但是不能用ps->arr接收返回值,因为arr数组空间变为NULL,会使得arr空间原本可能会有数据消失,出现数据丢失的情况,因此我们创建一个新的临时变量tmp来接收开辟空间返回的地址;(3)realloc的返回值类型是void*,因此需要tmp需要强制类型转换为SLDataType*。
2. 增容需要申请多大的空间?(增容的原则)
增容规则:增容通常来说,成倍数增加,一般是2、3倍。这个规律涉及概率论(补充:为什么增容需要以倍数增加?)比如,插入数据如果 是一个一个进行插入的,每插入一个数据就申请一块空间,当需要插入的数据很多时,就会出现频繁增容的情况,造成程序性能低下。最好的解决办法就是空间一次增加许多,但又不能增加太大,避免空间浪费;也不能增加太小了,所以2、3倍增加。如:4-8-16-32-64-128-256-512-1T……(2倍增加的)
如果插入的数据量不大,前期就能表现出来,因为数据个数和空间大小成正比。如果前期的数据量不确定,先少一点申请空间,若发现插入的数据比较多,就逐步扩大空间。
3. 使用三目操作符有什么作用?
起初在对顺序表进行初始化的时候,对capacity赋的值就是0,0无论乘以多少倍的容量值都是0;此外 ,如果capacity不等于0,那么就给它赋值4,这样newCapacity就等于2 * ps->capacity;如果capacity等于0,说明,ps指向的空间的空间容量为0。
4. 为什么还要判断tmp==NULL?
判断tmp得到的返回值是否为NULL,也就是判断动态申请空间是否成功。空间申请成功后需要将tmp赋值给需要空间的结构体,然后capacity的值变成newcapacity。
5. exit(1)和return 1的区别?
(1)exit(): 关闭所有文件,终止正在执行的进程。
a. exit是系统调用级别的 ,它表示了一个进程的结束,用于在程序运行过程中随时结束程序, exit的参数是返回给os操作系统的,exit是结束一个进程,它将删除进程使用的内存空间,同时把错误信息返回父进程;通常情况:在整个程序中,只要调用exit就结束(当前进程或者在main时候为整个程序)。
b. exit 是一个函数,exit是操作系统提供的(系统函数库中给出的)。
c. exit() 则会立即结束整个程序的执行,且不会返回到调用者。
(2)return()是返回函数值并退出当前函数。
a. return是语言级别的,它表示了调用堆栈的返回; return()是返回函数值并退出当前函数,当然如果是在主函数main, 自然也就结束当前进程了,如果不是,那就是退回上一层调用。在多个进程时。如果有时要检测上个进程是否正常退出。就要用到上个进程的返回值,依次类推。
b. return返回函数值,是关键字 ,是C语言提供的。
c. return 只会结束当前的函数,且如果是在子函数中使用,程序其余部分还会继续执行。
总的来说,exit(1)和return 1在这里都是差不多的效果,只是exit会比return更加暴力一些。
三、TOP-K问题
3.1 应用场景及其详细分析
TOP-K问题分析的是像某市区排名前十的富豪 这种可以将场景抽象成N个数中找到最大的前K个的问题。
像这种类似的场景一般就是先建立一个N个数的大堆,时间复杂度为O(N),然后再 Pop k-1次,时间复杂度为O(k*logN),(Pop中的向下调整算法使得每次Pop出去的都是最大值,Pop 9次是因为第10次就可以直接去获取堆顶元素即可)。但是这种方法的缺陷存在一定的缺陷。

这三种方法在时间上的效率都差不多,但是在空间上的消耗完全不同,可以根据需要进行调整。
3.2 深入讨论
Q:会不会有一个很大的数据堵在堆顶,使得后面的数据不能进堆?
A:不会。因为这里建立的是一个小堆,最终只会是第K个大数堵在堆顶,而且这K个数不是有序的。(可以让它再走一层排序,将其排成有序)
3.3 文件模拟验证TOP-K问题
//文件模拟验证TOP-K问题
void CreateNDate()
{// 造数据int n = 10000;srand((unsigned int)time(NULL));const char* file = "data.txt";FILE* fin = fopen(file, "w");if (fin == NULL){perror("fopen error");return;}for (size_t i = 0; i < n; ++i){int x = rand() % 1000000;//给不同的种子,让每次产生的随机数足够随机//rand产生的随机数是有重复的,因此我们加了一个i,大大减少了重复的随机数的产生fprintf(fin, "%d\n", x);//将随机数写进文件}fclose(fin);
}void PrintTopK(int k)
{const char* file = "data.txt";FILE* fout = fopen(file, "r");if (fout == NULL){perror("fopen fail");return;}int* kminheap = (int*)malloc(sizeof(int) * k);if (kminheap == NULL){perror("malloc fail");return;}//从文件读取前K个数据for (int i = 0; i < k; i++){fscanf(fout, "%d", &kminheap[i]);}//建立一个K个数的小堆(但是要先从文件中读取这前K个数)for (int i = (k - 1 - 1) / 2; i >= 0; i--){AdjustDown(kminheap, k, i);}//读取剩下的N-K个数int x = 0;while (!feof(fout))//feof是文件结束的标识,如果返回1,则说明文件结束{fscanf(fout, "%d", &x);//fscaf的光标闪动到原先的位置,所以会从k的位置开始读if (x > kminheap[0]){kminheap[0] = x;AdjustDown(kminheap, k, 0);}}for (int i = 0; i < k; i++){printf("%d ", kminheap[i]);}printf("\n");
}
int main()//该方法实现堆的顺序打印
{CreateNDate();PrintTopK(5);return 0;
}喜欢的uu记得三连支持Harper.Lee哦!

这篇关于DS:堆的应用——两种算法和TOP-K问题的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





