本文主要是介绍判断给定的数组是否为二叉搜索树的后序遍历序列,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题意描述:输入一个整数数组,判断该数组是不是某个二叉搜索树的后序遍历的结果。如果是则返回true,否则返回false。假设输入的数组的任意两个数字都互不相同。例如输入{5,7,6,9,11,10,8}返回true;输入{7,4,6,5}返回false
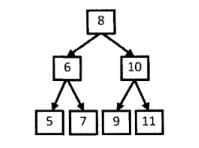
解题思路:在后序遍历序列中,最后一个数字是树的根结点的值,前面的数字可分为两个部分:第一部分是左子树,值都比根值小;第二部分是右子树,值都比根大。按些规律,依次判断,如果数组处理完毕则是后序遍历序列,否则不为后序遍历序列
(Java版)
boolean VerifySequenceOfBST(int[] sequence, int start, int end) { if(sequence == null || (end-start)<=0)return true;int root = sequence[end-1];int i = start;for(; i < end-1; i++)if(sequence[i] > root)break;int j = i;for(; j < end-1; j++)if(sequence[j] < root)return false;//判断左、右子序列是不是满足二叉搜索树boolean left = true;if(i > start)left = VerifySequenceOfBST(sequence, start, i);boolean right = true;if(i < end - 1)right = VerifySequenceOfBST(sequence, i ,end-1-i);return (left && right);
}(C++版)
bool VerifySequenceOfBST(int sequence[], int length) {if (sequence == NULL || length <= 0)return false;int root = sequence[length - 1];//在二叉搜索树中左子树的结点值小于根结点值int i = 0;for (; i < length - 1; i++) {if (sequence[i] > root)break;} //在二叉搜索树右子树的结点值大于根结点值int j = i;for (; j < length - 1; j++) {if (sequence[j] < root)return false;}//判断左子树是不是二叉搜索树bool left = true;if (i > 0)left = VerifySequenceOfBST(sequence, i);//判断右子树是不是二叉搜索树bool right = true;if (i < length - 1)right = VerifySequenceOfBST(sequence + i, length - i - 1);return (left && right);
}(Golang版)
func isBinaryTreePostOrder(arr []int) bool {if len(arr) == 0 || len(arr) == 1 {return true}lastEle := arr[len(arr)-1]posIdx := 0for ; posIdx < len(arr); posIdx++ {if arr[posIdx] > lastEle {break}}i := posIdxfor ; i < len(arr); i++ {if arr[i] < lastEle {return false}}left := isBinaryTreePostOrder(arr[0:posIdx])right := isBinaryTreePostOrder(arr[posIdx:len(arr)-1])return left && right
}
这篇关于判断给定的数组是否为二叉搜索树的后序遍历序列的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




