本文主要是介绍我的 Serverless 实战 - 第一个Serverless应用(附演示视频),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
写在前面:博主是一只经过实战开发历练后投身培训事业的“小山猪”,昵称取自动画片《狮子王》中的“彭彭”,总是以乐观、积极的心态对待周边的事物。本人的技术路线从Java全栈工程师一路奔向大数据开发、数据挖掘领域,如今终有小成,愿将昔日所获与大家交流一二,希望对学习路上的你有所助益。同时,博主也想通过此次尝试打造一个完善的技术图书馆,任何与文章技术点有关的异常、错误、注意事项均会在末尾列出,欢迎大家通过各种方式提供素材。
- 对于文章中出现的任何错误请大家批评指出,一定及时修改。
- 有任何想要讨论和学习的问题可联系我:zhuyc@vip.163.com。
- 发布文章的风格因专栏而异,均自成体系,不足之处请大家指正。
我的 Serverless 实战 - 第一个Serverless应用
本文关键字:腾讯云、Serverless、控制台、SpringBoot、应用部署
文章目录
- 我的 Serverless 实战 - 第一个Serverless应用
- 一、Serverless介绍
- 1. 什么是Serverless
- 2. Serverless的特点
- 二、第一个Serverless应用
- 1. 创建流程
- 2. 访问测试
- 三、视频直达
一、Serverless介绍
不少小伙伴可能对于Serverless还不太了解,先来做一下简单的介绍。
1. 什么是Serverless
随着技术的更新和开发模式的不断变化,企业中越来越多的使用到云资源,并且期望较为快速稳健的应用部署和功能迭代。很多功能直接通过整合云端服务实现,平台的部署也越来越多的应用到微服务架构和容器(如:Docker)。
从功能支持的角度来说,Serverless = FaaS + BaaS(图片来源于网络):
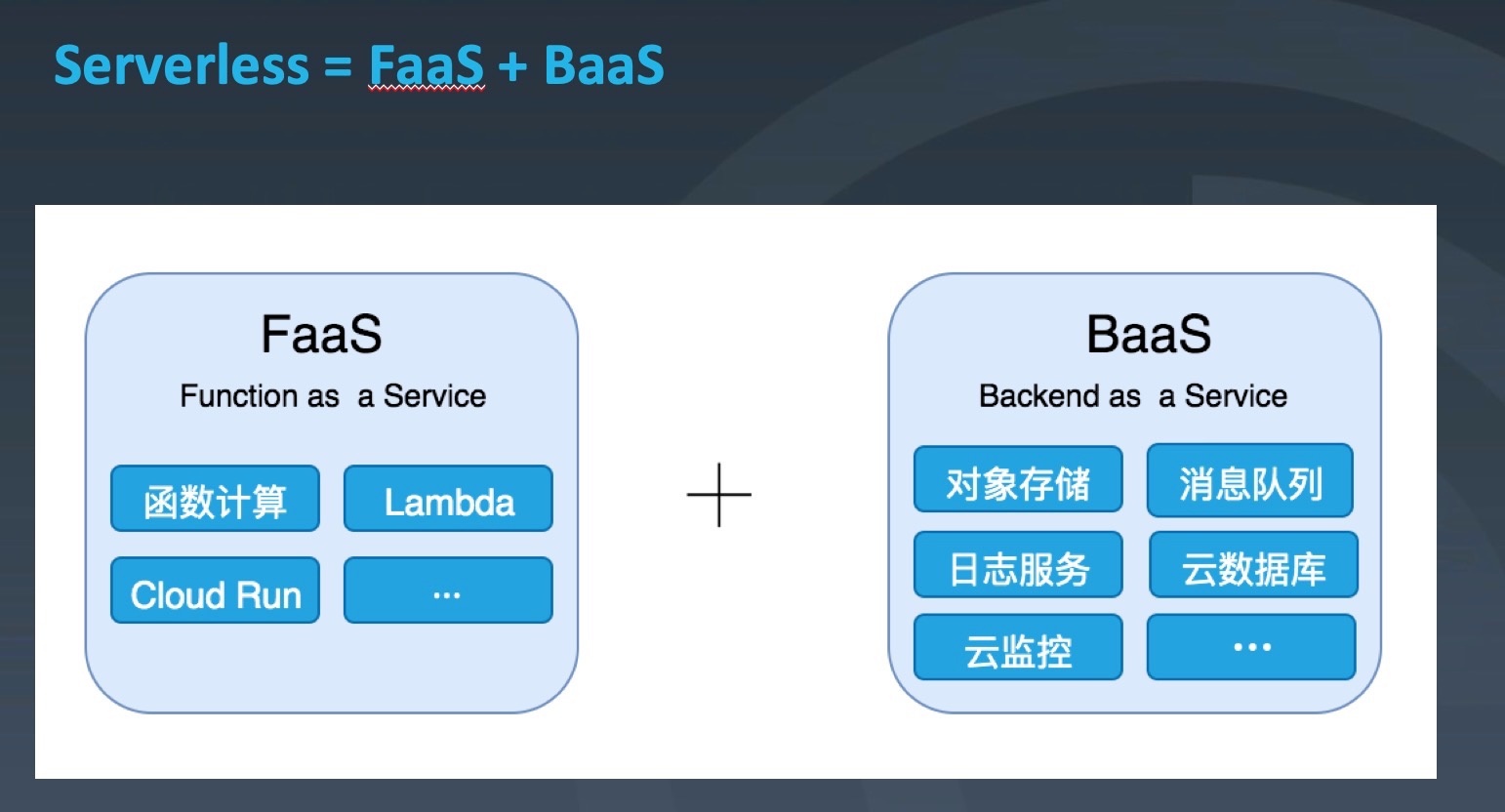
- FaaS(Function as a Service - 功能即服务):
主要包含云函数相关服务及平台。
- BaaS(Backend as a Service - 后端即服务):
主要包含后端云服务,如:云数据库、对象存储等。
- Serverless
以PaaS(Platform as a Service - 平台即服务)为基础,提供的一个微型架构,不需要再部署、配置或管理服务器服务,应用运行所需要的服务器服务皆由云端平台来提供。
2. Serverless的特点
- 简化配置
可以通过配置,对云函数、API网关、对象存储、云数据库等资源的创建、部署、和修改。
- 方便运维
支持按需付费,并且能够根据业务请求自动进行弹性伸缩,不需要再提前手动配置计算资源。
- 一站开发
支持从初始化、编码、调试、资源配置、部署发布到监控警告、故障排查的完整解决方案。
- 成本更低
使用成本低,费用的支付与函数的运行相关,尽可能不产生浪费。
二、第一个Serverless应用
使用Serverless应用控制台可以快速完成应用的创建和部署。
1. 创建流程
- 进入Serverless应用界面 -> 点击新建应用

- 选择模板(以SpringBoot为例)
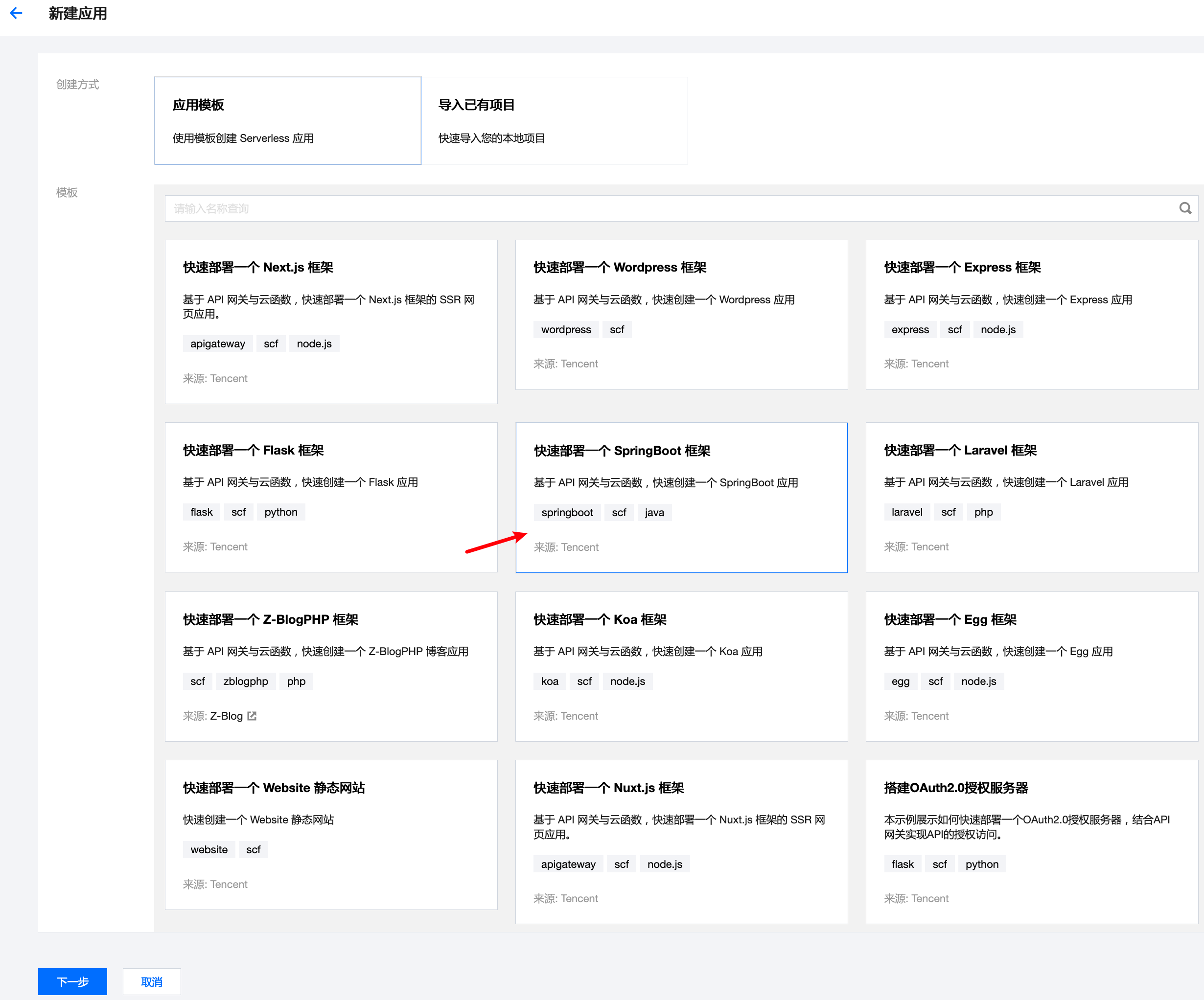
- 填写配置
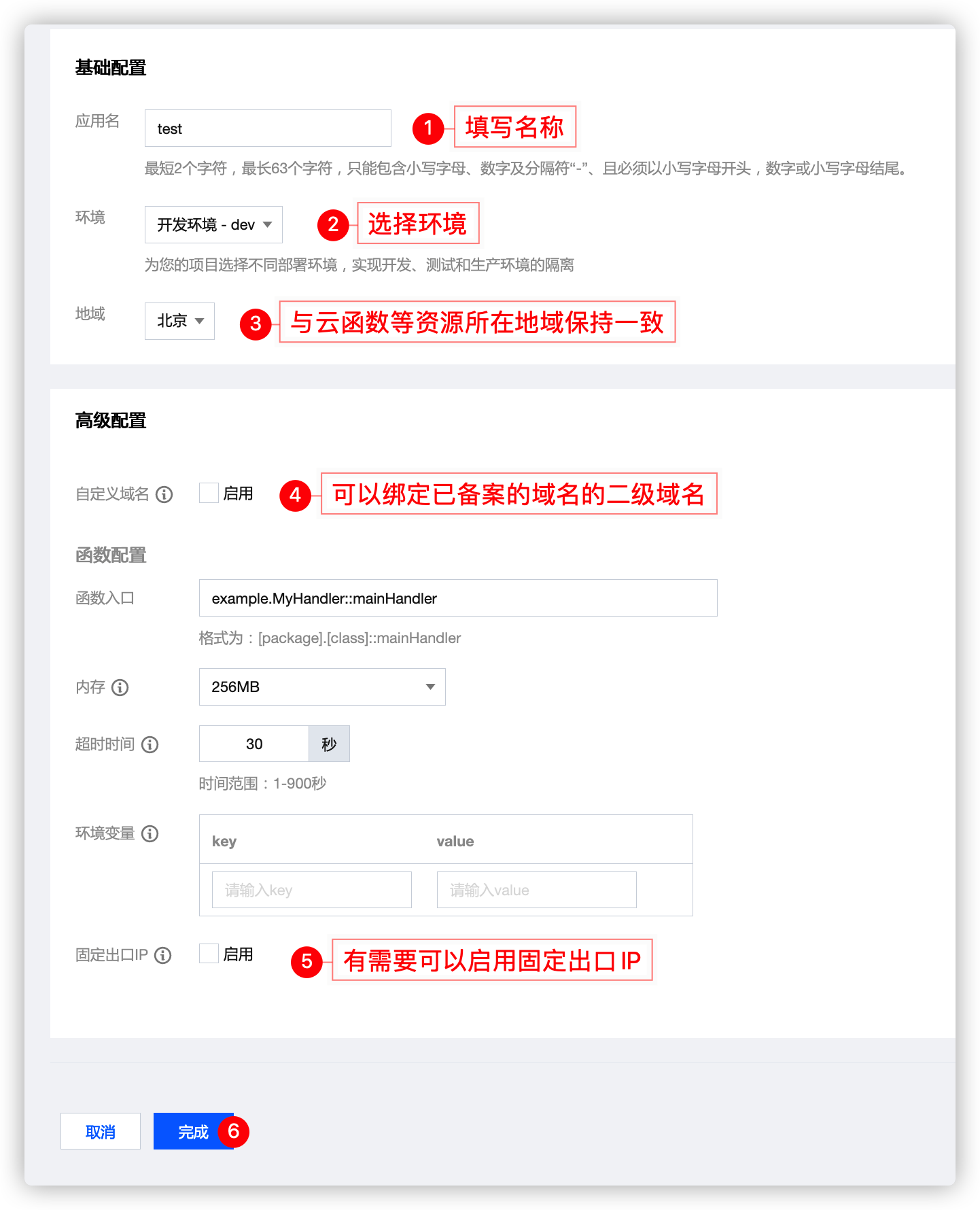
- 等待部署完成
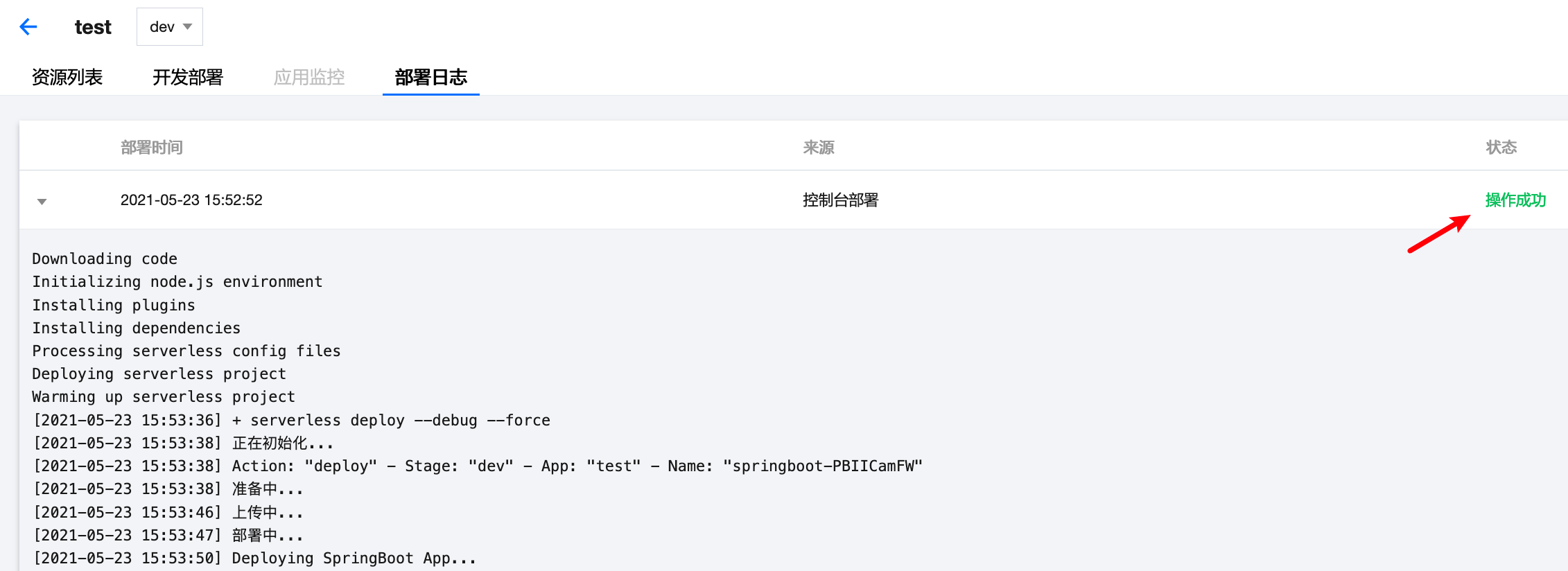
2. 访问测试
部署日志显示操作成功后,即可以对项目进行访问,来到Serverless应用界面可以查看到应用列表:
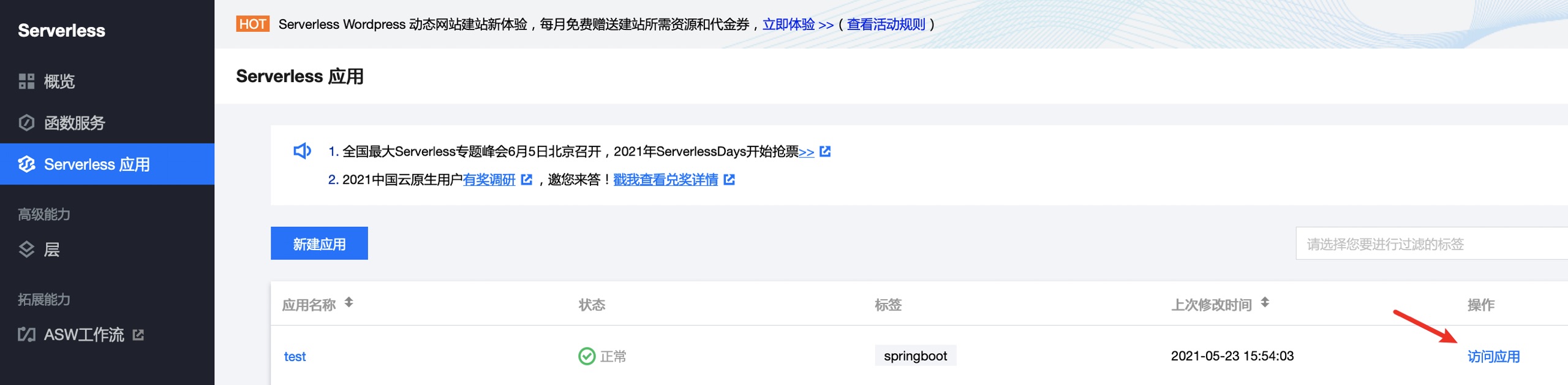
点击访问应用:

在应用的开发部署界面中可以进行应用的更新,会在后面的文章中介绍。
三、视频直达
视频地址:https://www.bilibili.com/video/BV1sq4y1E7cF,喜欢的小伙伴儿一定要三连加关注哦~
Serverless - 第一个Serverless应用
写在结尾:作者力求做到将每个知识点细化,并且对于有关联的知识点都会使用传送门挂载链接。文章采用:“文字 + 配图 + 视频”的方式来进行展现,均是挤时间所作,希望看到这里能留下评论点个赞,略表支持!
扫描下方二维码,加入官方粉丝微信群,可以与我直接交流,还有更多福利哦~

这篇关于我的 Serverless 实战 - 第一个Serverless应用(附演示视频)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






