本文主要是介绍推荐系统《Field-aware Factorization Machines for CTR Prediction》 论文精读,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
之前一篇文中说提到了FFM,那么我们今天就来看看FFM是个什么东西,它和FM又是什么关系。
摘要:点击率预测在计算机广告中有着重要的作用。在这个应用中,二阶多项式映射和因子分解模型应用的非常广泛。最近,各种种类的因子分解机(FM),领域因子分解机(FFM)在各个点击率预测的竞赛中表现出了其他模型都好的效果。基于我们获胜的经验,本文我们建立了对大型的稀疏数据集进行点击率预测的方法FFM。首先,我们提出了训练FFM的有效的方法,然后,我们对FFM进行了分析,并对比了其他的模型。经验表明,FFM对特定的数据集的效果非常的好,最后,我们发布了一个FFM的包。
1. 介绍
逻辑回归是点击率预测的使用非常广泛的模型,比如说一个数据集有m个样本,是输入特征,是对应的标签值,参数可以通过最小化下面的式子来得到:
其中,是正则化项,损失函数中的线性模型表示为:
对于点击率预测来说,特征之间的组合是非常重要的,我们考虑这样一个数据集,如下图:
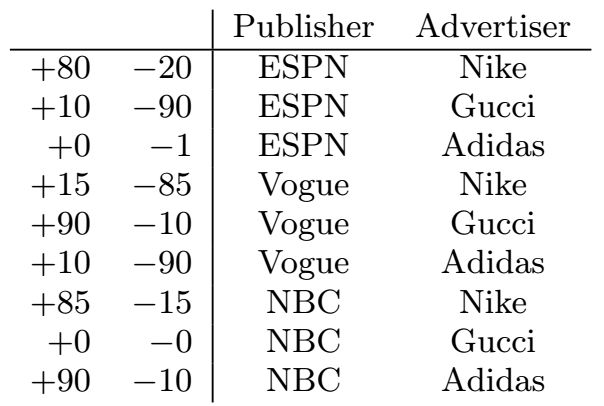
从数据集中可以看到,Gucci的广告在Vogue上有着非常高的点击率,这个用线性模型是没办法学到的,因为这两个变量相互是独立的。为了解决这个问题,提出了两个模型。一个是二阶的多项式映射模型,可以学习两两的组合的特征的参数,第二个是因子分解机,通过分解出隐含特征向量来学些特征间的相互关系。
FFM的一个变体,叫做Pairwise Interaction Tensor Factorization(PITF),用来对个性化的标签进行推荐。在KDD Cup 2012上,PITF的泛化形式“因子分解模型”被提出来。由于名字容易和因子分解机混淆,在这篇文中我们叫这个方法为领域因子分解机(FFM)。FFM和PITF的不同点在于,FFM更加的通用,而PITF只考虑了3个不同的领域,“用户”,“物品“和”标签“。
本文的目的是建立FFM模型用在点击率预测上,主要的结论如下:
我们展示了赢得两个推荐算法比赛的FFM模型
我们将FFM和两个模型进行了对比,FM和Poly2
我们展示了如何进行FFM的训练,包括并行优化和提前停止防止过拟合
我们发布了开源的算法实现
实验代码和工具包如下:
http://www.csie.ntu.edu.tw/~cjlin/ffm/expshttp://www.csie.ntu.edu.tw/~cjlin/libffm
2. Poly2和FM
Poly2可以利用特征间的组合进行建模,通过使用一个线性模型对特征间的组合进行建模,可以比使用核方法更快。这种方法就是Poly2,学习的是特征对的权重。
这个式子的时间复杂度是()。
FM学习每个特征的隐含向量,每个隐含向量有k维,特征组合的权值由隐含向量的内积得到。
变量的数量是n×k,直接计算的时间复杂度是()。将式子变换一下:
$$
$$
其中
这样,时间复杂度就变为()。
3. FFM
FFM的思想起源于PITF,是用在个性化标签的推荐系统上的。在PITF中,使用了3个不同的领域,用户、物品、标签。FFM更加的通用,可以使用更多的字段,而且用在了点击率的预测上。FFM是一个利用了领域信息的FM的变体,为了解释原理,我们使用下面的例子:
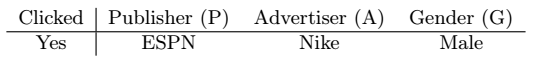
如果使用FM,可以表示为:
在FM中,每个领域由一个特征向量表示,通过和其他邻域特征的内积来表示两个领域特征的组合。然而,由于Nike和Male属于不同的领域,隐含特征对(ESPN,Nike)和(ESPN,Male)的作用很可能是不同的。
在FFM中,每个领域特征由多个特征向量组成,和不同的领域特征进行组合时,使用不同的向量:
写成数学的形式:
其中,和分别表示了和的领域。如果是领域的个数的话,那么FFM的变量的总的个数是。时间复杂度是(),但是在FFM中,通常k会比FM中小的多。
3.1 求解最优化问题
我们可以使用梯度下降的方式求解FFM,最近提出了一些自适应学习率的优化方式,我们这里使用了AdaGrad,这个方法用在因子分解上和FFM上效果不错。
初始化的参数从均匀分布中采样,采样范围是。算法流程如下:

3.2 并行化和共享内存系统
使用多个CPU并行计算,每个CPU独立进行计算。
3.3 增加领域信息
考虑我们常用的LIBSVM的数据格式:
label feat1:val1 feat2:val2 · · · ,
每个特征对(feat:val)表示了特征的索引和值。对于FFM,我们将这种数据格式进行扩展:
label field1:feat1:val1 field2:feat2:val2 · · ·
这样的话,我们需要为每个特征赋予一个领域字段,这对有些特征很容易,而对有些则比较麻烦,我们分三个不同类型的特征来讨论
类别特征
对于线性模型来说,表示类别的特征通常会进行离散化,并转换成几个二值特征。对于一个数据样本:
Yes P:ESPN A:Nike G:Male,
我们可以生成如下的LIBSVM数据格式:
Yes P-ESPN:1 A-Nike:1 G-Male:1
类别的数量是多少,就会生成多少个二值的特征,但是只有其中的一个为1,其余的都是0,在LIBSVM的数据格式中,值为0的特征是不需要写出来的。我们在所有的模型上都是这样使用的,本文中,我们将每个类别特征分解成几个二值特征,然后为每个二值特征加上领域字段。
Yes P:P-ESPN:1 A:A-Nike:1 G:G-Male:1
数值特征
我们考虑下面的数据集,预测一个文章是否能被会议接收。我们使用了3个数值特征,“会议的接受率”,“作者的h索引”,“作者的引用数量”。
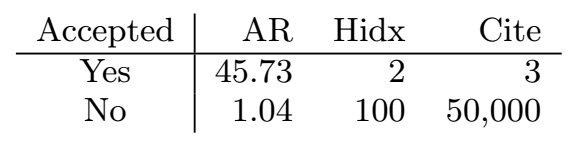
有两个方法来赋值领域,一个方法是将每个特征作为一个dummy的领域,生成的数据如下:
Yes AR:AR:45.73 Hidx:Hidx:2 Cite:Cite:3
而这些dummy的领域并不提供什么信息,因为只是赋值了特征的名字而已。
另一个方法就是对数值离散化,然后再分成不同的类别,再按类别数据的方式进行处理。生成的数据如下:
Yes AR:45:1 Hidx:2:1 Cite:3:1,
其中AR被四舍五入成整数,不过这种方式的缺点在于,我们很难找到合适的离散化的方式,比如说我们可以将45.73变换成45.7,45,40等等甚至是int(log(45.73)),另外,这样做会损失一点信息。
单领域特征
有些数据集中,所有的数据都是属于同一个领域的,比如NLP的场景,考虑下面的例子,通过一句话来预测这句话表达的情绪。
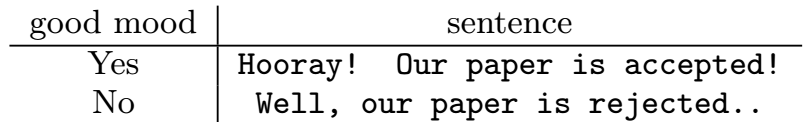
这个例子中,唯一的领域就是句子,如果我们将这个领域赋值给所有的单词,那么FFM就变成了FM。FFM的复杂度是,使用dummy的领域是不现实的,因为f=n,而n是很大的。
4. 实验
在这部分,我们会先提供我们实验中的一些细节的设置,然后我们会研究超参数的影响。我们发现,和LM和Poly2不同的是,FFM对于epoch的数量很敏感,我们会详细的讨论这个问题,然后我们会用一个提前停止训练的trick,然后再说一说并行化的加速。
然后我们会对比不同的算法,包括FM和Poly2,还有比较不同的实现包,包括LIBLINEAR和LIBFM。
4.1 实验设置
数据集
我们主要考虑Kaggle上的两个点击率预测的数据集Criteo和Avazu,特征工程我们使用了比赛中的方案,见http://github.com/guestwalk/kaggle-2014-criteo and http://github.com/guestwalk/kaggle-avazu 。我们使用了哈希的方式产生了个特征,数据集的统计值如下:
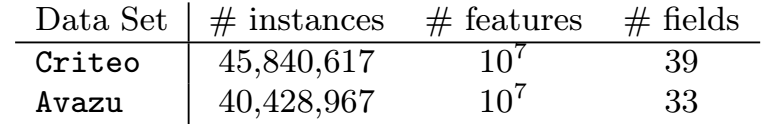
由于测试集没有标注数据,我们在已有的数据上划分训练集、验证集。
平台
实验平台为Intel Xeon E5-2620 2.0GHz处理器 和 128 GB 内存
评估
根据使用不同的模型,我们将变为,,,,我们使用下面的logistic损失函数:
实现
我们使用c++实现了所有的算法,使用了OpenMP来进行并行化。我们的实现包括了线性项和偏置项。为了保持扩展性,不管使用什么模型,领域信息都会存在模型里。对于非FFM模型,不存储领域信息也许会快那么一点点,但是结果应该都是一样的。
4.2 参数的影响
我们进行了实验来研究不同的参数影响,这些参数包括,,,具体的结果可以见下图:
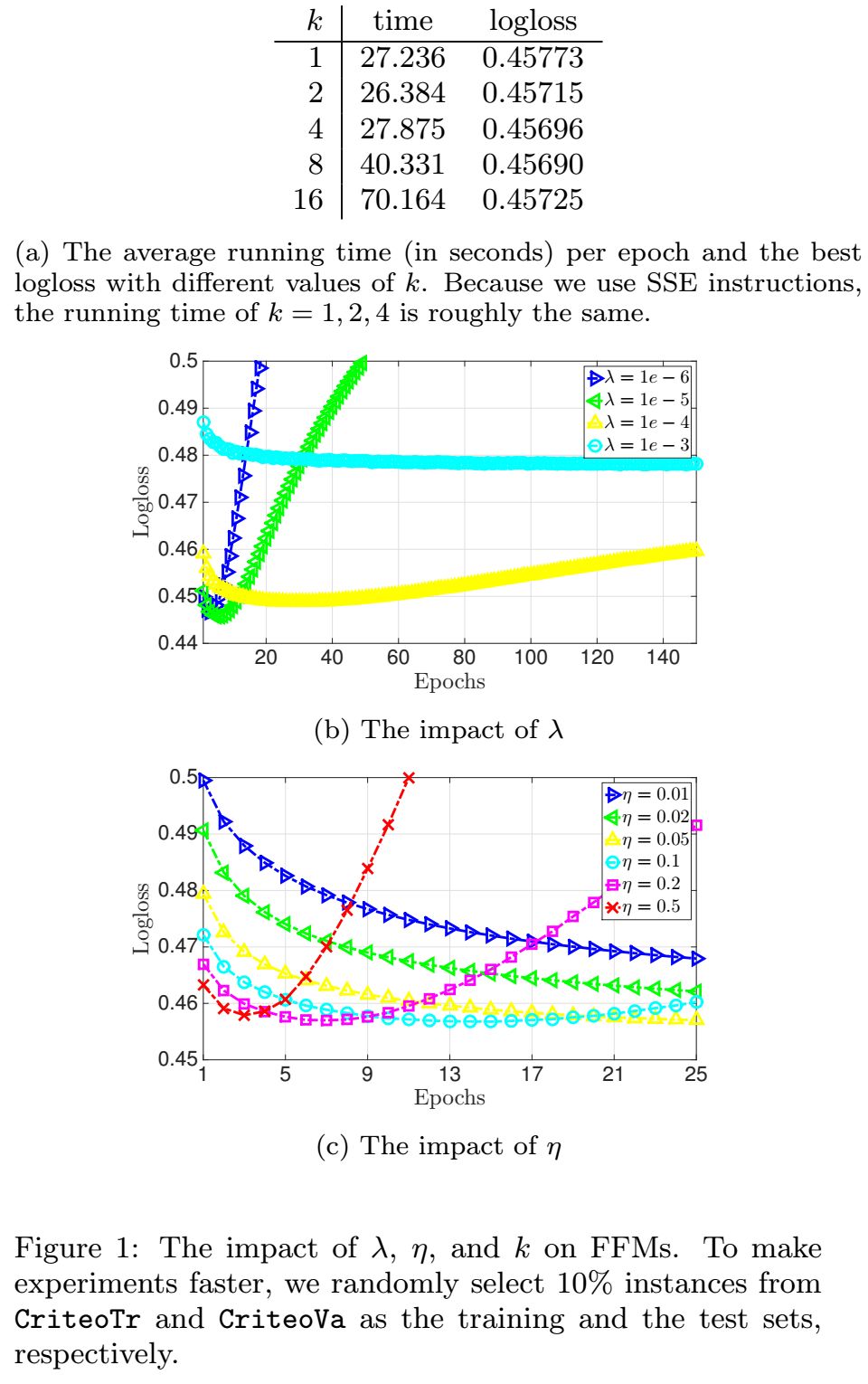
从图中的曲线中可以看出,很多情况下的参数设置可能会出现过拟合的现象,因此,需要进行early stop的操作。
4.3 Early Stop
Early Stop是指在训练的过程中,在还没有达到最佳的结果之前就停止掉,可以用来防止过拟合。对于FFM,我们使用的策略如下:
将数据集划分成训练集和验证集
每个epoch结束之后,计算验证集的loss
如果loss变大了,记录下当前的epoch数,然后到第4步
如果需要,使用所有的数据重新训练模型,epoch的数量用第三步记录的epoch数
early stopping用起来很难,是因为logloss对于epoch数量很敏感,在验证集上最好的模型,在测试集上未必表现的最好。我们也用了一些其他的防止过拟合的方法,都不如early stopping好。
4.4 加速
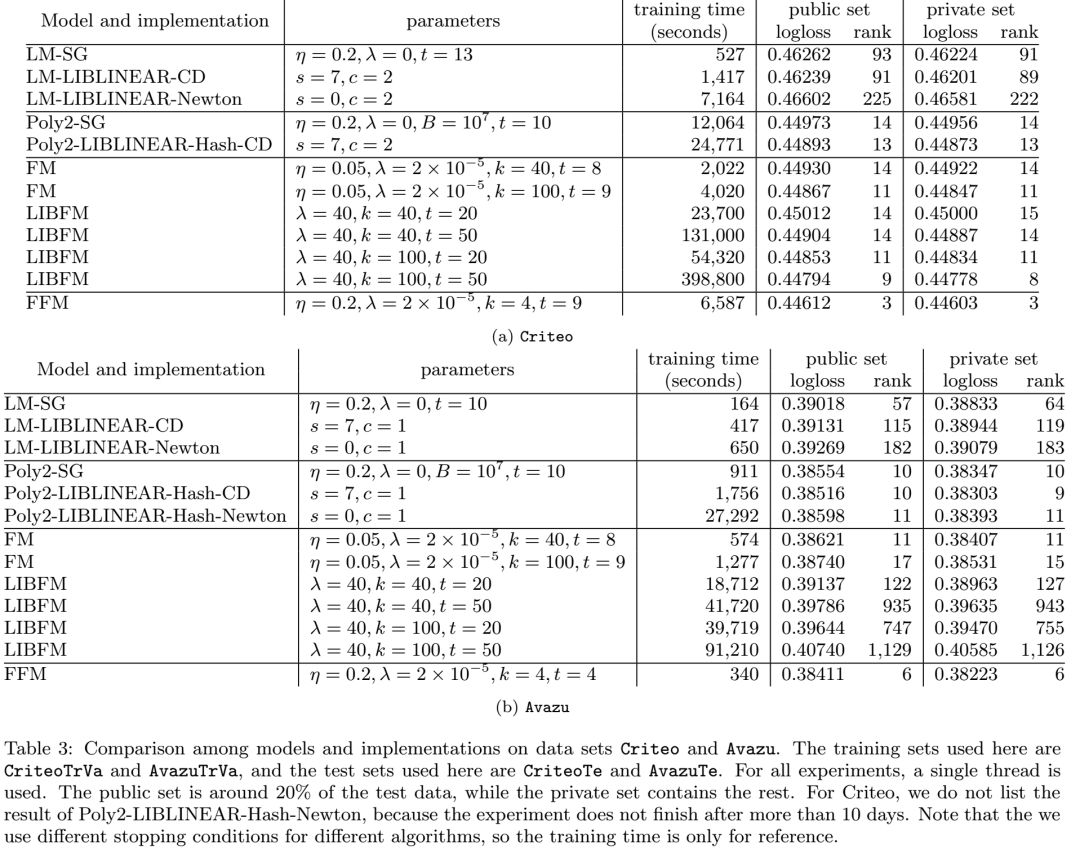
4.5 和LM,Poly2,FM模型的对比
我们使用同样的梯度下降的方法,对比了另外的3个模型,然后,我们对比了两个业界领先的包:LIBLINEAR和LIBFM。结果如下:
4.5 和其他数据集的对比
在其他的数据集上的对比:
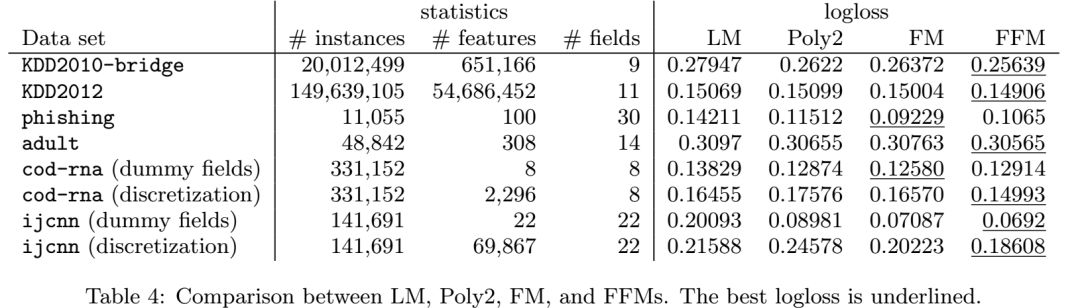
我们总结了将FFM应用在其他的数据集的一些指南:
FFM在有不同类别,并且可以转换成二值特征的数据集上是很有效的。
如果数据集经过变换之后,稀疏程度不是很高,那么FFM的好处就不是很多。
在数值特征的数据集上,FFM的效果不是很好。
5. 结论
这篇关于推荐系统《Field-aware Factorization Machines for CTR Prediction》 论文精读的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







