卷积神经网络感受野计算指南

点击上方“AI公园”，关注公众号，选择加“星标“或“置顶”

作者：Dang Ha The Hien

编译：ronghuaiyang

之前分享过一篇文章，是关于感受野的，今天这篇文章是专门讲解如何计算感受野的，可以和之前那篇结合起来看，之前那篇文章我也再推送一次给大家。

感受野可能是卷积神经网络(CNNs)中最重要的概念之一，值得更多的关注。所有最先进的物体识别方法都围绕这一思想设计它们的模型体系结构。然而，据我所知，目前还没有一个完整的指南，如何计算和可视化感受野的CNN信息。这篇文章通过介绍一种新的方法来填补这一空白，这种方法可以在CNN中可视化特征图，公开感受野信息，同时提供一个完整的感受野计算，可以用于任何CNN架构。我还实现了一个简单的程序来演示计算，这样任何人都可以开始计算感受野，并更好地了解他们正在使用的CNN的架构。

为了理解这篇文章，我假设您熟悉CNN的概念，特别是卷积和池操作。你可以通过阅读论文"A guide to convolution arithmetic for deep learning"来更新你的CNN知识。如果你对CNNs有一定的了解，这篇文章不会占用你超过半个小时。这篇文章实际上是受到那篇论文的启发，并使用了类似的符号。

固定尺寸的CNN特征图可视化

感受野 定义为输入空间中某个CNN特性正在查看(即受其影响)的区域。特征的感受野可以通过其中心位置和大小来描述。然而，并不是感受野中的所有像素对于其对应的CNN特征都是同等重要的。在感受野内，像素越靠近中心，对输出特征的计算贡献越大。这意味着一个特征不仅关注输入图像中的一个特定区域(即它的感受野)，而且指数级地更加关注该区域的中心。这一重要见解将在另一篇博客文章中进一步解释。目前，我们的重点是计算特定感受野的位置和大小。

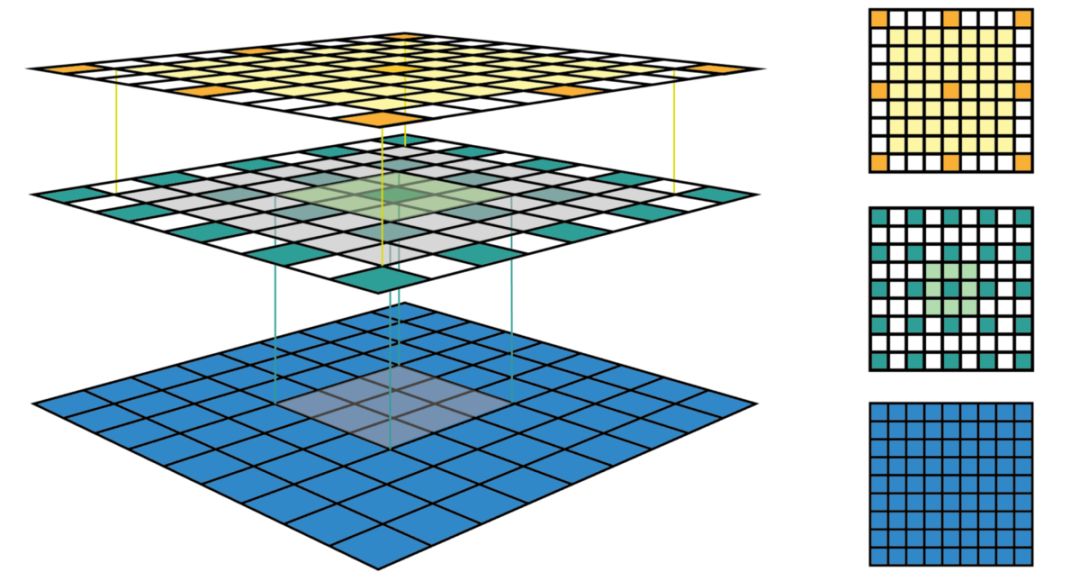
图1显示了一些感受野示例。将C与kernel size k = 3x3， padding size p = 1x1， stride s = 2x2 *在输入map 5x5上进行卷积，得到输出feature map 3x3(绿色map)。在3x3 feature map上应用相同的卷积，得到2x2feature map(橙色map)。每个维度中输出特性的数量可以使用以下公式计算，具体说明如下。

注意，在本文中，为了简化，我假设CNN架构是对称的，而输入图像是正方形的。所以这两个维度对于所有变量都有相同的值。如果CNN架构或输入图像是非对称的，则可以分别计算每个维度的feature map属性。

图1的左列显示了一种可视化CNN feature map的常用方法。在这个可视化过程中，尽管通过查看特征图，我们知道它包含了多少特征。不可能知道每个特征观察的位置在哪里(它的感受野的中心位置)，以及这个区域有多大(它的感受野大小)。图1的右栏显示了固定尺寸的CNN可视化，它通过保持所有feature map的大小不变并等于输入map来解决这个问题。每个特征都被标记在其感受野位置的中心。因为feature map中的所有特征都具有相同大小的感受野，所以我们可以简单地在一个特征周围画一个包围框来表示它的感受野大小。我们不需要将这个边界框一直映射到输入层，因为feature map已经在输入层用相同大小来表示了。图2显示了另一个使用相同卷积的例子，但应用于更大的输入映射- 7x7。我们可以用3D(左)或2D(右)绘制固定大小的CNN feature maps。注意，图2中感受野的大小增长得非常快，以至于第二个特性层的中心特征的感受野几乎覆盖了整个输入map。这是一个重要的见解，它被用来改进一个深度CNN的设计。

感受野计算

要计算每一层的感受野，除了每个维度的特征数n外，还需要跟踪每一层的一些额外信息。其中包括当前感受野大小r，两个相邻特征(或跳转)之间的距离j，和左上角特征(第一个特征)的中心坐标start 。注意，特征的中心坐标被定义为其感受野的中心坐标，如上面的固定大小的CNN feature map所示。当与kernel size k， padding size p， stride size s进行卷积时，输出层的属性可以通过以下公式计算：

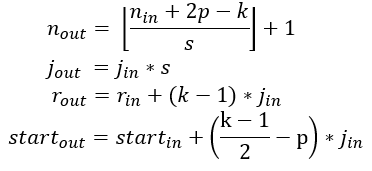
• 第一个方程根据输入特征个数和卷积性质计算输出特征个数。这与上面中给出的方程相同。

• 第二个方程计算输出特征图中的jump，它等于输入映射中的jump乘以应用卷积时跳过的输入特征的数量(步长)。

• 第三个方程计算输出feature map的接感受野大小，等于k 个输入特征所覆盖的区域(k-1)*j_in，加上边界上输入feature的感受野所覆盖的额外区域。

• 第四个方程计算第一个输出特征的感受野的中心位置，等于第一个输入特征的中心位置 + 第一个输入特征的中心位置到第一个卷积 (k - 1) / 2 * j_in的距离 - padding空间p * j_in。注意，在这两种情况下，我们都需要将输入feature map的jump相乘，以得到实际的距离/空间。

第一层是输入层，它总是有n =图像大小，r = 1， j = 1， start = 0.5。注意，在图3中，我使用的坐标系中，输入层的第一个特征的中心位于0.5。通过递归应用上述四个方程，我们可以计算出CNN中所有feature map的感受野信息。图3显示了这些方程如何工作的示例。

我还创建了一个小型python程序，它计算给定CNN体系结构中所有层的感受野信息。它还允许你输入任何特征图的名称和该特征图中特征的索引，并返回相应感受野的大小和位置。下图显示了使用AlexNet时的输出示例。代码在本文末尾提供。

# [filter size, stride, padding]	
#Assume the two dimensions are the same	
#Each kernel requires the following parameters:	
# - k_i: kernel size	
# - s_i: stride	
# - p_i: padding (if padding is uneven, right padding will higher than left padding; "SAME" option in tensorflow)	
# 	
#Each layer i requires the following parameters to be fully represented: 	
# - n_i: number of feature (data layer has n_1 = imagesize )	
# - j_i: distance (projected to image pixel distance) between center of two adjacent features	
# - r_i: receptive field of a feature in layer i	
# - start_i: position of the first feature's receptive field in layer i (idx start from 0, negative means the center fall into padding)	
import math	
convnet =   [[11,4,0],[3,2,0],[5,1,2],[3,2,0],[3,1,1],[3,1,1],[3,1,1],[3,2,0],[6,1,0], [1, 1, 0]]	
layer_names = ['conv1','pool1','conv2','pool2','conv3','conv4','conv5','pool5','fc6-conv', 'fc7-conv']	
imsize = 227	
def outFromIn(conv, layerIn):	n_in = layerIn[0]	j_in = layerIn[1]	r_in = layerIn[2]	start_in = layerIn[3]	k = conv[0]	s = conv[1]	p = conv[2]	n_out = math.floor((n_in - k + 2*p)/s) + 1	actualP = (n_out-1)*s - n_in + k 	pR = math.ceil(actualP/2)	pL = math.floor(actualP/2)	j_out = j_in * s	r_out = r_in + (k - 1)*j_in	start_out = start_in + ((k-1)/2 - pL)*j_in	return n_out, j_out, r_out, start_out	
def printLayer(layer, layer_name):	print(layer_name + ":")	print("\t n features: %s \n \t jump: %s \n \t receptive size: %s \t start: %s " % (layer[0], layer[1], layer[2], layer[3]))	
layerInfos = []	
if __name__ == '__main__':	
#first layer is the data layer (image) with n_0 = image size; j_0 = 1; r_0 = 1; and start_0 = 0.5	print ("-------Net summary------")	currentLayer = [imsize, 1, 1, 0.5]	printLayer(currentLayer, "input image")	for i in range(len(convnet)):	currentLayer = outFromIn(convnet[i], currentLayer)	layerInfos.append(currentLayer)	printLayer(currentLayer, layer_names[i])	print ("------------------------")	layer_name = raw_input ("Layer name where the feature in: ")	layer_idx = layer_names.index(layer_name)	idx_x = int(raw_input ("index of the feature in x dimension (from 0)"))	idx_y = int(raw_input ("index of the feature in y dimension (from 0)"))	n = layerInfos[layer_idx][0]	j = layerInfos[layer_idx][1]	r = layerInfos[layer_idx][2]	start = layerInfos[layer_idx][3]	assert(idx_x < n)	assert(idx_y < n)	print ("receptive field: (%s, %s)" % (r, r))	print ("center: (%s, %s)" % (start+idx_x*j, start+idx_y*j))

英文原文：https://medium.com/mlreview/a-guide-to-receptive-field-arithmetic-for-convolutional-neural-networks-e0f514068807

请长按或扫描二维码关注本公众号

喜欢的话，请给我个好看吧！