DSP 中数字下变频的基础知识

本文主要是介绍DSP 中数字下变频的基础知识，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

本文讨论数字下变频，这是一种广泛用于数字无线电接收器的数字信号处理技术。

数字下变频是一种数字信号处理技术，广泛用于数字无线电接收机。本文将回顾数字下变频器 (DDC) 的基础知识。我们将首先了解使用 DDC 而不是模拟对应物的优势。然后，我们将讨论一个示例并探索 DDC 的基本操作。

要了解使用 DDC 的优势，让我们首先回顾一下传统的双下变频接收器并检查其缺点。基本的双下变频接收器如图 1 所示。如您所见，在信号被模数转换器 (ADC) 数字化之前有几个模拟块。

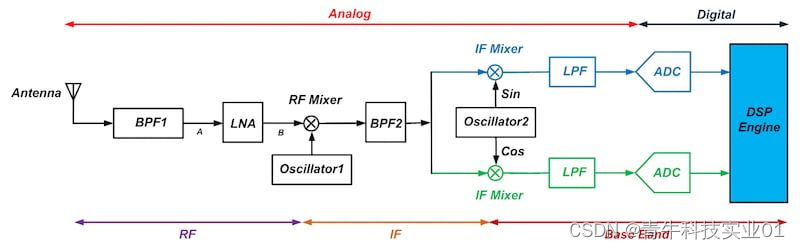
图 1. 点击放大。

以下部分回顾了上述接收器中使用的每个块的基本功能。如果您熟悉 RF 工程的基础知识，则可以通过下一节来刷新您的知识；否则，您可能需要先阅读 AAC 的RF 教科书中的一些页面。

基本双下变频接收器

在图 1 的接收器中，个带通滤波器 BPF1 为个混频器执行镜像抑制，在图中标记为“RF 混频器”。它还部分抑制了天线拾取的干扰源。这放宽了低噪声放大器 (LNA) 的线性度要求。

带通滤波器的输出由 LNA 放大。与所需信号相比，这种放大使得后续级产生的噪声相对较小。这样，接收器对 LNA 之后级的噪声变得不那么敏感。

然后， RF 混频器将节点 B 处的放大信号下变频为中频$$f_{IF}$$。

现在所需信号已下变频到较低频率，我们可以更轻松地构建一个相对高 Q 的滤波器 BPF2，并部分执行通道选择。请注意，由于接收器的双下变频结构，个混频器的中频 $$f_{IF}$$ 可以相对较高。这放宽了 BPF1 的要求。

接下来，信号通过由振荡器 2 驱动的正交混频器（见图 1）。振荡器 2 的频率等于 $$f_{IF}$$，因此所需频带的中心频率将转换为 DC。这意味着我们不需要用于 IF 混频器的镜像抑制滤波器。

接下来我们通过基带低通滤波器 (LPF) 进行通道选择，，ADC 将所需信号数字化，结果将由数字信号处理器 (DSP) 进一步处理。DSP 引擎将执行均衡、解调和通道解码等操作。

传统收音机的弊端及解决方案

我们可以考虑图 1 中所示的双下变频接收器的三个主要限制：

两条基带路径必须高度匹配。蓝色路径中的 IF 混频器、LPF 和 ADC 必须与绿色路径中的相应组件匹配。
模拟滤波器引入了相位失真。
ADC 注入一个 DC 项，该项不能轻易从所需信息中删除。请注意，图 1 的 IF 混频器将所需通道的中心频率转换为 DC，其中 ADC 可以注入误差项。该 ADC 偏移量可由其构建模块（例如放大器和比较器）的偏移量产生。即使零信号应用于 ADC，偏移项也会导致非零数字代码。这对于以极低频率传送信息的系统非常重要。

我们可以在接收器的 DSP 部分弥补这些缺陷；然而，更好的解决方案是将 A/D 转换器放在接收器链中的正交混频器之前。如图 2 所示。

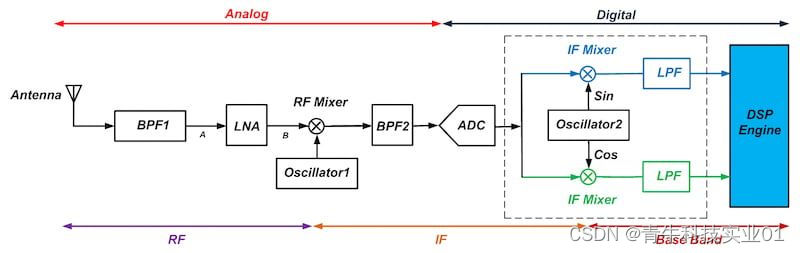
图 2. 点击放大。

如您所见，现在 A/D 转换发生在 IF 而不是基带。这意味着 ADC 必须以更高的采样率运行。如图所示，ADC之后的block都工作在数字域。例如，图2中振荡器2的输出实际上是正弦和余弦信号对应的数字值。为了实现振荡器 2，我们通常使用直接数字合成器(DDS)。第二次下变频是使用两个数字乘法器执行的，LPF 是数字滤波器。

如上所述，对于图 2 的结构，ADC 必须以更高的采样率运行。这可能被认为是一个缺点，但 DDC 方法也提供了显着的好处：

现在，IF 混频器和 LPF 是数字电路。因此，消除了由模拟组件之间的不匹配引起的与不平衡相关的失真。
与模拟领域不同，我们可以轻松设计线性相位数字滤波器。
在信号通过 IF 混频器之前，ADC 注入的 DC 项可以很容易地被数字滤波器去除（有关示例，请参见《无线通信和广播中的数字前端》第 12 章）。

请注意，虽然图 2 在接收器的 DSP 引擎之外具有正交混频器和 LPF，但我们当然可以在系统的 DSP 平台内实现这些块。此外，在基带 LPF 之后，我们可以在不丢失所需信息的情况下显着降低采样率（有关更多信息，请参阅我关于多速率 DSP 及其在 A/D 转换中的应用的文章）。因此，我们可以重新绘制图 2 的虚线框内的电路，如图 3 所示。此模块称为数字下变频器或 DDC。

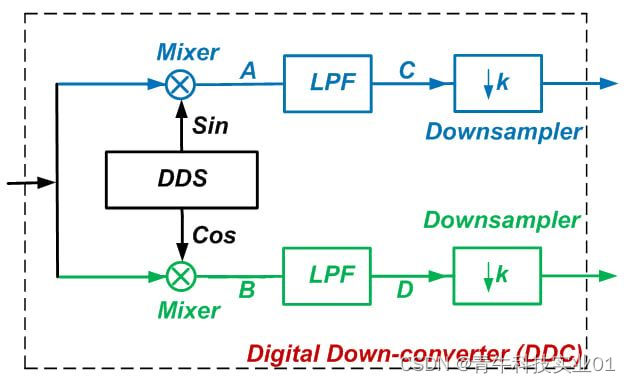
图 3

数字下变频

假设经过模数转换后，所需信号的频谱如图 4 所示。

图 4

所需信号的中心频率为 110 MHz，带宽为 4 MHz（图中显示了正频率和负频率）。此外，我们假设 ADC 以 440 MSPS（每秒百万样本）的速率生成样本。DDC 将如何处理这个输入？

DDC 使用的 DDS 将生成 110 MHz 正弦和余弦信号。这些正弦和余弦函数中的每一个都会导致 $$\pm 110$$ MHz 的脉冲。由于时域中的乘法对应于频域中的卷积，因此对于图 3 中的节点 A 和 B，我们将得到图 5 所示的频谱。

图 5

如您所见，$$\pm 110$$ MHz 的频移已将图 4 的蓝色频谱转换为 220 MHz 和 DC。类似地，绿色频谱转移到 DC 和 -220 MHz。我们能够对节点 A 和 B 使用一个图，因为这两个节点具有相同的幅度特性，图 5 仅传达了幅度谱。节点 A 的相位谱将不同于节点 B 的相位谱。

在图 5 中，请注意下变频后信号边带在 DC 周围重叠。考虑到这种重叠，我们是否可以仅使用以 DC 为中心的频谱部分来恢复所需的信息？我们可以; 我们正在使用正交混合，它会生成两个相同的幅度谱，但也会生成两个不同的相位谱，重叠区域的相位谱使我们能够恢复原始信息。由于这种重叠不是问题，高于 2 MHz 的频率分量不会提供任何必要的信息，因此我们可以在数字混频器之后放置一个 LPF，以仅保留低于 2 MHz 的频率分量。这种低通滤波在图 3 中描绘为单级滤波器，通常作为两级滤波器实现，如图 6 所示。