本文主要是介绍2021数学建模C题目– 生产企业原材料的订购与运输,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
C 题——生产企业原材料的订购与运输
思路:该题主要是通过对供应商的供货能力和运送商的运货能力进行估计,给出合适的材料订购方案
程序获取
备用
第一题问题思路与结果:
对 402 家供应商的供货特征进行量化分析,建立反映保障企业生产重要性的数学模型, 在此基础上确定 50 家最重要的供应商,并在论文中列表给出结果。
这一题主要是希望可以对402家供应商的供货能力进行分析对比从而选出50家供应商,因此需要对供应商过去5年的数据进行分析和评分,分析的内容包括
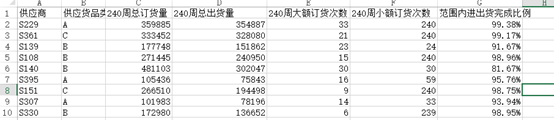
- 供应商的被要求订货数量
- 供应商最终达到的供应量
- 供应商供货的完成的情况
- 等等
第二题问题思路与结果:
该企业应至少选择多少家供应商供应原材料才可能满足生产的需求?针对这些供应商, 为该企业制定未来 24 周每周最经济的原材料订购方案,并据此制定损耗最少的转运方案。 试对订购方案和转运方案的实施效果进行分析。
对过去5年48周数据进行分析制定了进货测量和送货策略
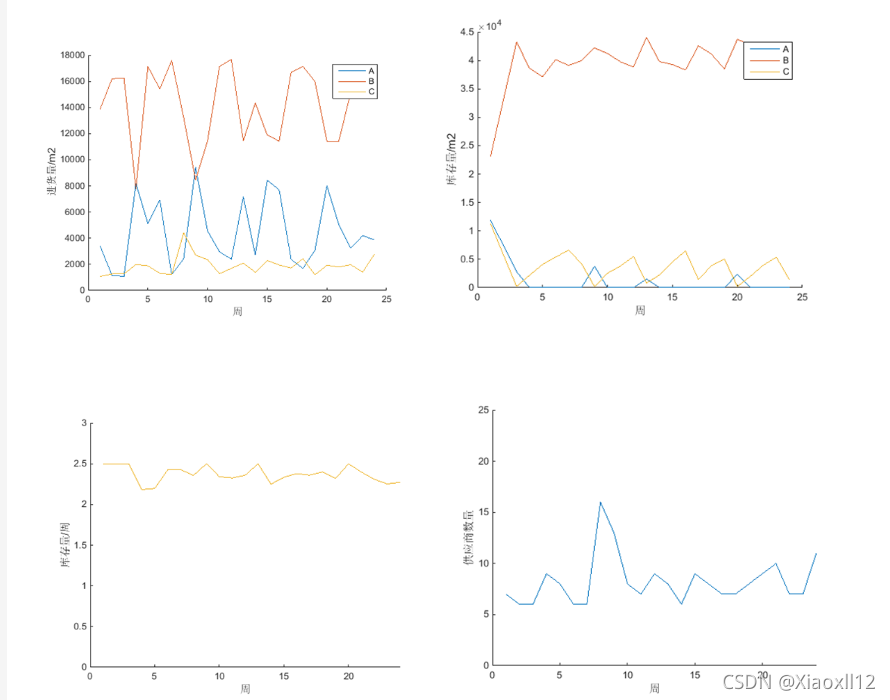

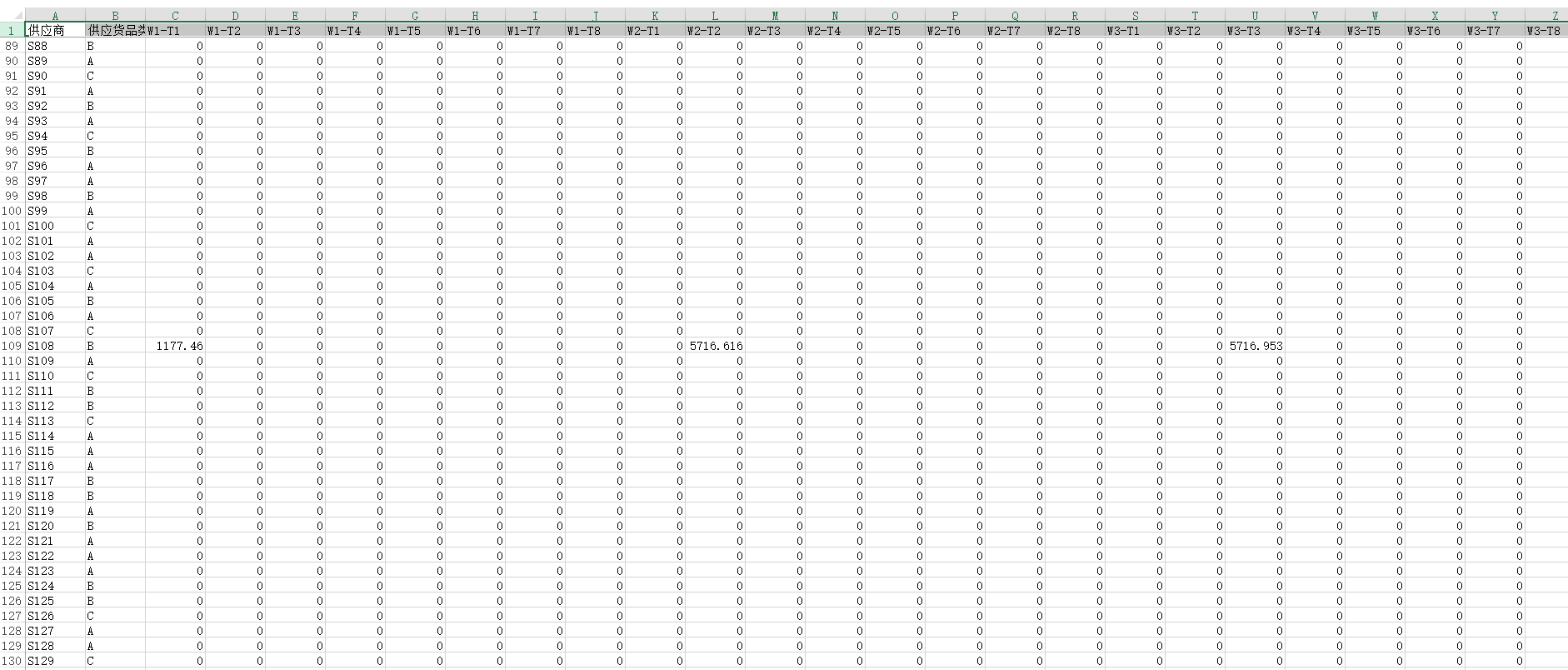
第三题问题思路与结果:
该企业为了压缩生产成本,现计划尽量多地采购 A 类和尽量少地采购 C 类原材料,以减少转运及仓储的成本, 同时希望转运商的转运损耗率尽量少。 请制定新的订购方案及转运方案,并分析方案的实施效果。
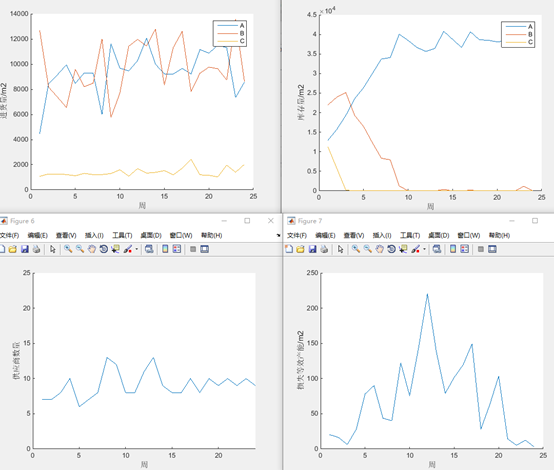
两个思路可以降低C的采购,一个是使用库存时,优先用C类材料,最后使用A类材料,另一个是采购时对供应商进行重新排序优先采购A类材料的供应商的材料,
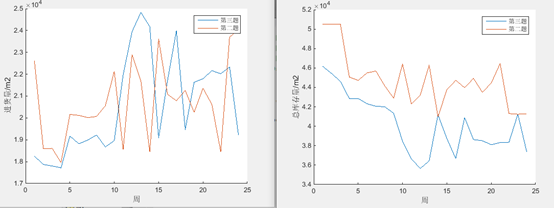
可以看出库存体积明显下降,其他部分结果如下
第四题问题思路与结果:
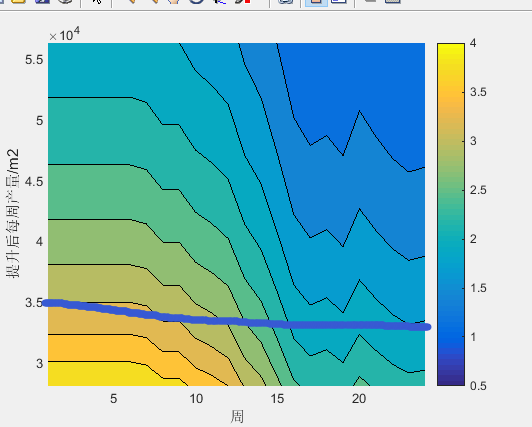
该企业通过技术改造已具备了提高产能的潜力。根据现有原材料的供应商和转运商的实际情况, 确定该企业每周的产能可以提高多少, 并给出未来 24 周的订购和转运方案
可以设置一个较高的初始库存,然后逐步提高产能,看24周后的剩余库存,找到可以满足库存大于2周的最大产能即可,

这篇关于2021数学建模C题目– 生产企业原材料的订购与运输的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







