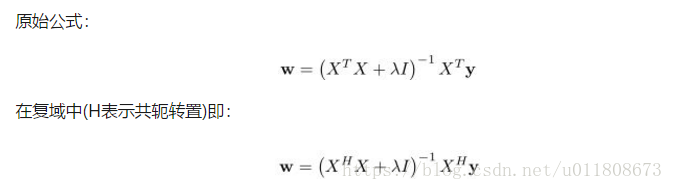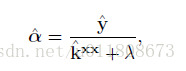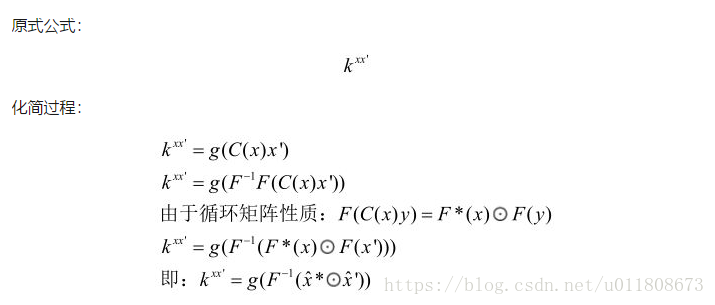KCF -目标检测算法总结

本文主要是介绍KCF -目标检测算法总结，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

KCF简介

KCF是一种鉴别式追踪方法，这类方法一般都是在追踪过程中训练一个目标检测器，使用目标检测器去检测下一帧预测位置是否是目标，然后再使用新检测结果去更新训练集进而更新目标检测器。而在训练目标检测器时一般选取目标区域为正样本，目标的周围区域为负样本，当然越靠近目标的区域为正样本的可能性越大。

简单来说 KCF 是 核相关滤波算法，滤波器 和 跟踪patch 进行相乘的到相关性，对应位置较大的值，相关性较强，即表示得到的目标位置。

KCF全称为Kernel Correlation Filter 核相关滤波算法。是在2014年由Joao F. Henriques, Rui Caseiro, Pedro Martins, and Jorge Batista提出来的，算法出来之后也算是轰动一时，这个算法不论是在跟踪效果还是跟踪速度上都有十分亮眼的表现，所以引起了一大批的学者对这个算法进行研究以及工业界也在陆续把这个算法应用在实际场景当中。这个算法主页里面有论文还有代码都可以在这里面下载，也有一些简介之类的，这篇文章在2015年作者又发在了TPAMI上面，所以大家可能会看到两个版本，但是没有改动，都是可以看到。论文下载地址相关滤波算法算是判别式跟踪，主要是使用给出的样本去训练一个判别分类器，判断跟踪到的是目标还是周围的背景信息。主要使用轮转矩阵对样本进行采集，使用快速傅里叶变化对算法进行加速计算。

KCF的主要贡献

• 使用目标周围区域的循环矩阵采集正负样本，利用脊回归训练目标检测器，并成功的利用循环矩阵在傅里叶空间可对角化的性质将矩阵的运算转化为向量的Hadamad积，即元素的点乘，大大降低了运算量，提高了运算速度，使算法满足实时性要求。

• 将线性空间的脊回归通过核函数映射到非线性空间，在非线性空间通过求解一个对偶问题和某些常见的约束，同样的可以使用循环矩阵傅里叶空间对角化简化计算。

• 给出了一种将多通道数据融入该算法的途径。

二、详细介绍

Abstract：主要介绍了一下这篇文章的想法的由来以及算法的成就和所使用的东西，还介绍了一下论文在哪些数据集上测试了等。简介一般就是论文的总结，对论文做一个总体的介绍，大致的思想基本看了间接之后就能明白了，就是上面我写的那些，使用核相关滤波器训练一个判别式分类器，使用轮转矩阵生成样本去训练分类器，代码也是开源的。

Correlation Filter应用于tracking方面最朴素的想法就是：相关是衡量两个信号相似值的度量，如果两个信号越相似，那么其相关值就越高，而在tracking的应用里，就是需要设计一个滤波模板，使得当它作用在跟踪目标上时，得到的响应最大，最大响应值的位置就是目标的位置。（详细的介绍大家可以参考一下王泥喜龙一的博客地址）如下图所示： 
 
CSK（论文下载地址）是这个算法改进的初级版本，这篇是主要引进了循环矩阵生成样本，使用相关滤波器进行跟踪，本篇KCF是对CSK进行更进一步的改进，引进了多通道特征，可以使用比着灰度特征更好的HOG（梯度颜色直方图）特征或者其他的颜色特征等。

2、Related Work

2.1、基于检测的跟踪 
这个听名字就比较好理解了，基于检测到的目标进行跟踪，首先在跟踪之前对目标进行检测，得到目标的位置，然后对目标进行学习，跟踪。 
2.2、样本转换和相关滤波 
对一些以前存在的样本转换的方法和相关滤波的一些知识进行一个介绍。For us, this hinted that a deeper connection between translated image patches and training algorithms was needed, in order to overcome the limitations of direct Fourier domain formulations.而且说出了样本和训练算法都是必须的，直接在频域使用傅里叶变化加快算法。 
2.3、后来的工作 
初始版本就是我上面说的CSK那篇，然后把多通道特征以及核函数这个加进来对算法进行提升。

3、Contributions

提出了一个快速的效果良好的跟踪算法，把以前只能用单通道的灰度特征改进为现在可以使用多通道的HOG特征或者其他特征，而且在现有算法中是表现比较好的，使用HOG替换掉了灰度特征，对实验部分进行了扩充，充分证明自己的效果是比较好的。使用核函数，对偶相关滤波去计算。

4、Building Blocks

4.1、 Linear regression 
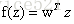
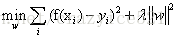
主要使用岭回归函数，能够像SVM那些有良好的表现。训练的目的就是找到这么一个函数使得我们的误差函数最小，在本文中使用的误差函数为 
接下来的一切内容都是去讲怎么去最小化这个二次函数，以及怎么去找这个函数，这个方法也是比较简单的，就是对函数求导，然后使导数等于0，然后得到w，既是我们要求的函数。

在线性问题中：

在求解这里的最小值的时候，将f(xi)根据公式（1）换成矩阵形式Wt*X（为什么可以转换成这种形式参考SVM），X的每一行表示一个采样结果的xi，X是经过第一行的xi不断循环得到的一个矩阵,Wt表示W的转置。y表示yi组成的向量。然后计算公式（2）对W的求导等于0可以得到：

（3）

 

（4）

（4）式即将（3）式中的转置转换成了共轭，只要是考虑在下面的傅里叶转换中有负数的出现。

这里我们看到在求w得最小值的时候有矩阵求逆的操作，这使得计算量比较大。然而根据之前说的X是一个循环矩阵，形式为：

（5）

将矩阵进行傅立叶变换后，循环矩阵有一个性质:

---

(6)

即一个循环矩阵可以用它的第一行的向量进行傅里叶变换之后表示，x带一个帽子表示对向量x进行了傅里叶变换。傅里叶变换的具体理解可以参考：此篇傅里叶博客

对于如何进行傅里叶转换可以参考：傅里叶转换方法

然后就可以发现一个循环矩阵可以转换成用一个向量来表示。将（6）式带入（4）式化简：

 

w戴帽子的意思就是进行了傅里叶转换，这样就从一个矩阵的运算换到了向量的运算。减少了求逆的操作。

当然在大多数情况下我们解决的是非线性问题：

那我们就引进了高维求解和 核函数的概念（仔细的求解参考上文提到的SVM文章）。

在高维空间中非线性问题w可以变成一个线性问题。

 

（7）

fai(xi)表示将x映射到高位空间的函数。

那我们的目标函数就可以表示成

（8）

其中k表示核函数它的定义运算如下：

由（8）可见之前求最小w的问题转换成了求最小阿尔法的问题。将（8）带入（2）阿尔法的求解参考一篇文章“R. Rifkin, G. Yeo, and T. Poggio, “Regularized least-squares classification,Nato Science Series Sub Series III Computer and Systems Sciences, vol. 190, pp. 131–154, 2003.”

最后可以解得

 

（9）

进行傅里叶变换：

这里Kxx代表K矩阵的第一行元素的傅里叶变换。K也是一个循环矩阵可证，此处省略具体方式可参考“High-Speed Tracking with Kernelized Correlation Filters João F. Henriques, Rui Caseiro, Pedro Martins, and Jorge Batista”的5.2节。

这样（8）式可以表示成：

C（x）表示由向量x循环移位得到的矩阵

Kz是所有训练样本和候补patch之间的核矩阵

（9）

傅里叶变换后的形式

现在就剩讨论一下k的形式，如果k是线性核的话就可以转换成我们在讨论线性问题时求得的w的傅里叶转换之后的形式。本篇文章中用的是高斯核，形式如下：

 

多通道问题

论文中在提取目标区域的特征时可以是灰度特征，但是使用Hog特征能够取得更好的效果，那么Hog特征该如何加入前面提到的模型呢？

Hog特征是将图像划分成较小的局部块，称为cell，在cell里提取梯度信息，绘制梯度方向直方图，然后为了减小光照影响，将几个cell的方向直方图串在一起进行block归一化，最终将所有的cell直方图串联起来就是图像的特征啦。

那么，按照传统的方式一张图像就提取出一个向量，但是这个向量怎么用啊？我们又不能通过该向量的移位来获得采样样本，因为，你想啊，把直方图的一个bin循环移位有什么意义啊？

所以论文中Hog特征的提取是将sample区域划分成若干的区域，然后再每个区域提取特征，代码中是在每个区域提取了32维特征，即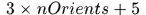,其中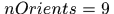就是梯度方向划分的bin个数，每个方向提取了3个特征，2个是对方向bin敏感的，1个是不敏感的，另外4个特征是关于表观纹理的特征还有一个是零，表示阶段特征，具体参见fhog。提取了31个特征(最后一个0不考虑)之后，不是串联起来，而是将每个cell的特征并起来，那么一幅图像得到的结果就是一个立体块，假设划分cell的结果是,那么fhog提取结果就是,我们成31这个方向为通道。那么就可以通过cell的位移来获得样本，这样对应的就是每一通道对应位置的移位，所有样本的第i通道都是有生成图像的第i通道移位获得的，
，所以分开在每一个通道上计算，就可以利用循环矩阵的性质了。

我们来看1D的情况，1D弄明白了，2D也就明白咯，因为我们上面说了怎么推导2D的
样本cell数为M，每个cell特征维数为L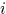,第个样本的第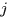通道向量表示成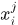,样本的总特征可以表示成.

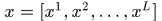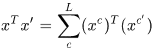
于是K矩阵的第一行有

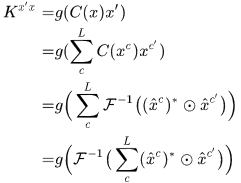
这里用到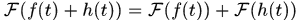

这是dot product kernel的情况，那径向基核就很容易推了

 

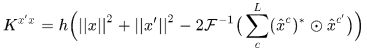
2.其实讲到这里已经把精髓讲完了，下面讲一些推导细节，加深理解。

2.1循环矩阵对角化有神奇效果，大大降低了运算量。首先举个例子，来展现它神奇的效果。就拿上文出现的岭回归公式当例子吧，看看能把它简化成什么样。

化简过程：

这是我早前推的，比起他的公式，我个人更喜欢他的代码嘻嘻。这个公式推下来并没有用，只是让我们见识一下循环矩阵化简的威力，真正用到代码里去的是下面3个推导。

 

2.2大家是否还记得我们这里实际上用到的是核化的岭回归啊？也就是比普通的稍微简化了一些的，所以推导起来也比较容易。

论文结果： 

嗯，好像看起来还不错哦，既没有求逆又没有很多矩阵乘法运算。它的代码其实更感人。

简单的不能再简单了，至此，训练过程结束。下面看检测过程，同样化简得面目全非。

 

2.3检测出跟踪结果，就是当前输入的帧和滤波器求相关性，相关性最大的即为跟踪结果。

嗯，这篇论文真是不断地感动着我们这些吃瓜群众，原来可以这么简单。看着公式，代码闭着眼睛都能编了。

 

现在只剩一个问题了，那就是核相关性怎么求。

2.4核相关性的化简。好像解决了这个就完美了，那这个核相关性好求吗？如果不好求的话，就空亏一篑了，放心，跟踪界的allstar Henriques（葡萄牙人的名字我至今不会读）当然已经帮我们解决好了，依然简单。

我们这里只推导点积核。剩下的多项式核，径向基核，高斯核类比就能得到。论文里效果最好的是高斯核。

 

注意，代码里第2行是使用HOG特征的关键，他把31层HOG特征全部加起来了，这个简单的操作使得之前的CSK能用很多高维特征，故性能大增。

 

补充

循环矩阵傅里叶对角化

文献中，一般用如下方式表达这一概念： 

 对角化怎么理解？

 

总结

KCF相对于其他的tracking-by-detection方法速度得到了极大的提升，效果也相对较好，思想和实现十分简单。

 

借上图来总结下KCF的过程，左图是刚开始我们使用红色虚线框框定了目标，然后红色实线框就是使用的padding了，其他的框就是将padding循环移位之后对齐目标得到的样本，由这些样本就可以训练出一个分类器，当分类器设计好之后，来到了下一帧图像，也就是右图，这时候我们首先在预测区域也就是红色实线框区域采样，然后对该采样进行循环移位，对齐目标后就像图中显示的那个样子 了，（这是为了理解，实际中不用对齐。。。），就是周围那些框框啦，使用分类器对这些框框计算响应，显然这时候白色框响应最大，因为他和之前一帧红色框一样，那我们通过白色框的相对移位就能推测目标的位移了。

然后继续，再训练再检测。。。。

论文中还说到几点

1. 对特征图像进行cosine window加权，这主要是为了减轻由于边界移位导致图像不光滑。

2. padding的size是目标框的2.5倍，肯定要使用padding窗口，要不然移位一次目标就被分解重组合了。。。效果能好哪去。。

3. 对于标签使用了高斯加权

4. 对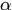前后帧结果进行了线性插值，为了让他长记性，不至于模型剧烈变化。

但是其缺点也是很明显的。

1. 依赖循环矩阵，对于多尺度的目标跟踪效果并不理想。当然可以通过设置多个size，在每个size上进行KCF运算，但这样的话很难确定应预先设置多少size，什么样的size，而且对size的遍历必将影响算法的速度。KCF最大的优势就是速度。

我在想能不能通过少量特征点的匹配来调整窗口的size，当然这样的话，速度也是个问题。

 

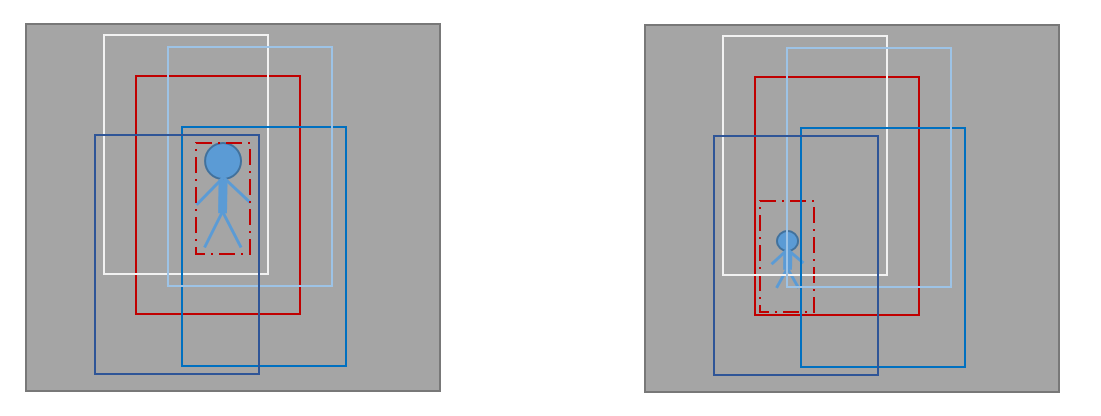
这种情况下还能保证最大响应就对应着目标中心所在的框吗？如果不能偏差会不会越来越大？

1. 初始化矩阵不能自适应改变，其实这个问题和上一个缺点类似，这里强调的是非刚体运动，比如跳水运动员，刚开始选定区域肯定是个瘦长的矩形框，但当运动员开始屈体的时候显然这个预选定框就很大误差了。

 

 

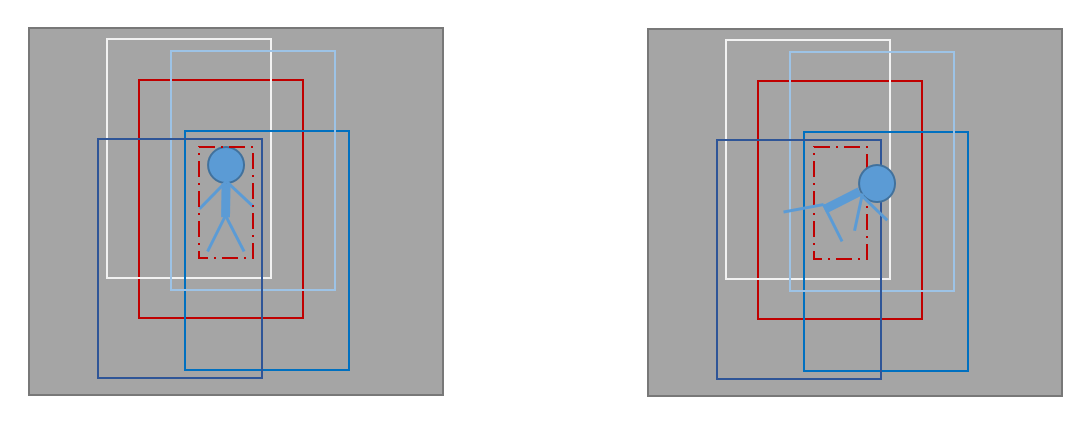
3.难处理高速运动的目标

1. 难处理低帧率中目标，这个和3类似，都是说相邻帧间目标位移过大。

 

 

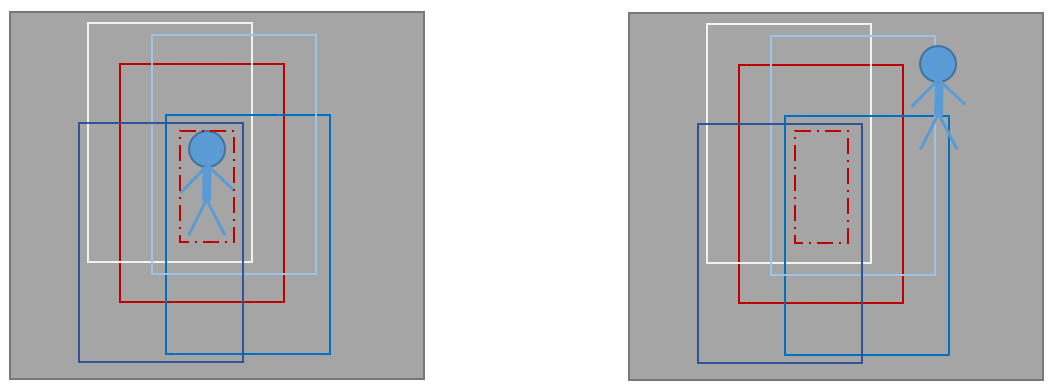
目标下一帧出现位置不在你的padding内，你怎么也不可能移位找到。。。

5.虽然算法中对模型系数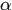进行线性插值，但是对于目标一旦被遮挡若干帧之后，可能模型就再也回不去了。。。因为模型已经完全被遮挡物污染掉了。

6.我觉的论文还有一个问题就是仅仅通过检测到的框中心和目标实际中心的距离来度量性能，这是有问题的。
比如我现在有一个人垂直我的镜头逐渐远去了，但他的中心一直在我镜头的中心处，那我就开始画个框就是镜头的视角范围，那这样我检测结果百分之百，可是有什么用呢。。。。当然论文方法是在很多不同数据集上检验的性能还是很有说服力的。我的意思就是对于单个数据集不能仅凭这个指标定方法的好坏。

 

引用：

https://blog.csdn.net/shenxiaolu1984/article/details/50884830

https://www.jianshu.com/p/9aacd075a689

https://zhuanlan.zhihu.com/p/26685032

https://www.cnblogs.com/YiXiaoZhou/p/5925019.html

https://blog.csdn.net/crazyice521/article/details/53525366

这篇关于KCF -目标检测算法总结的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---