本文主要是介绍【递归、搜索与回溯】记忆化搜索,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、经验总结
以斐波那契数为例引入今天的主角:记忆化搜索和动态规划
题目链接
509. 斐波那契数 - 力扣(LeetCode)
题目描述

算法原理
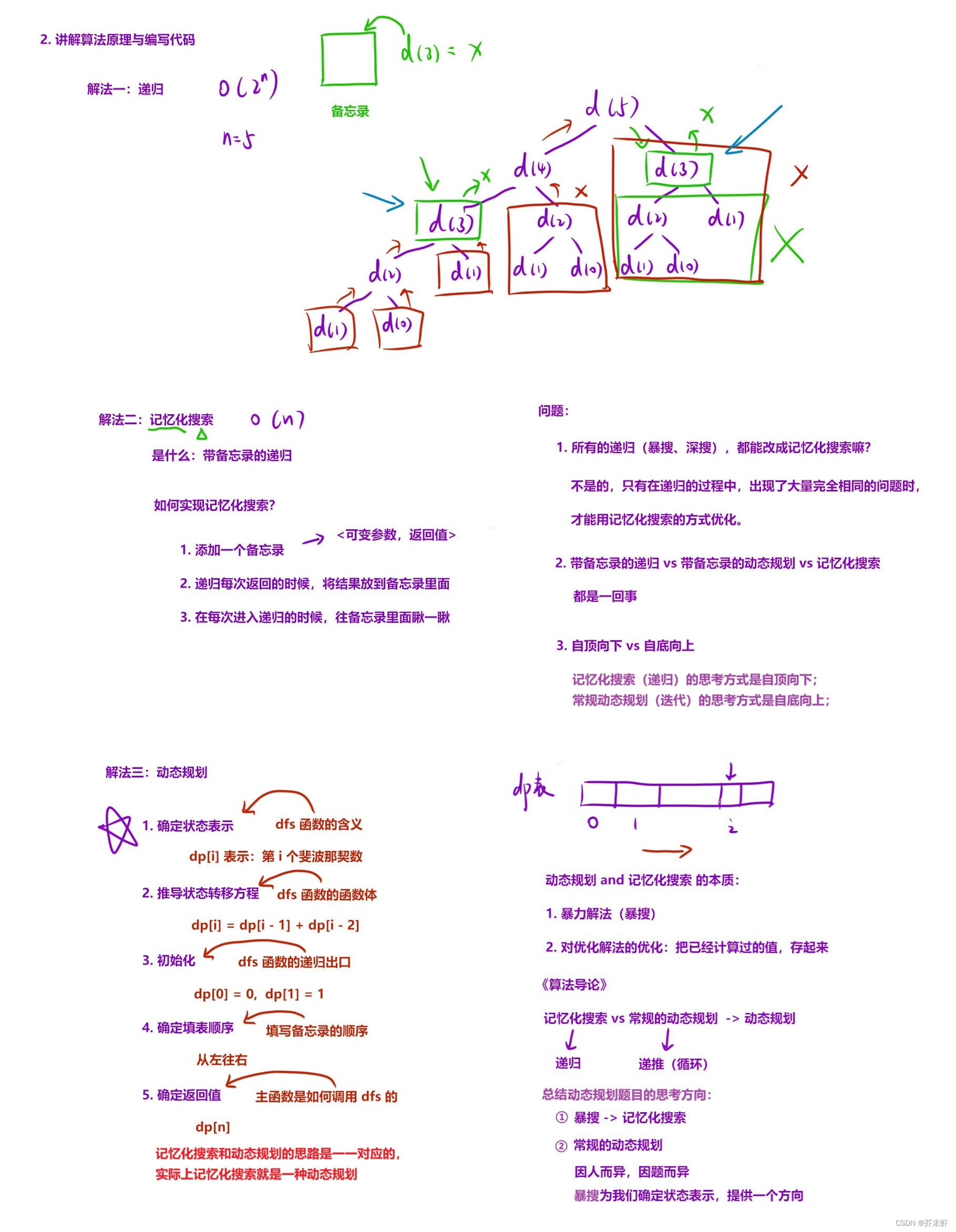
编写代码
//解法二:递归->记忆化搜索
class Solution {int mem[31]; //备忘录
public:Solution(){memset(mem, -1, sizeof(mem));}int fib(int n) {if(mem[n] != -1) return mem[n];if(n==0 || n==1) mem[n] = n; elsemem[n] = fib(n-1) + fib(n-2);return mem[n];}
};//解法三:动态规划
class Solution {int dp[31]; //dp[i]表示第i个斐波那契数
public:int fib(int n) {dp[0] = 0, dp[1] = 1; //初始化for(int i = 2; i <= n; ++i) //从右往左填表{dp[i] = dp[i-1]+dp[i-2]; //状态转移方程}return dp[n]; //返回值}
};
二、相关编程题
2.1 不同路径
题目链接
62. 不同路径 - 力扣(LeetCode)
题目描述

算法原理
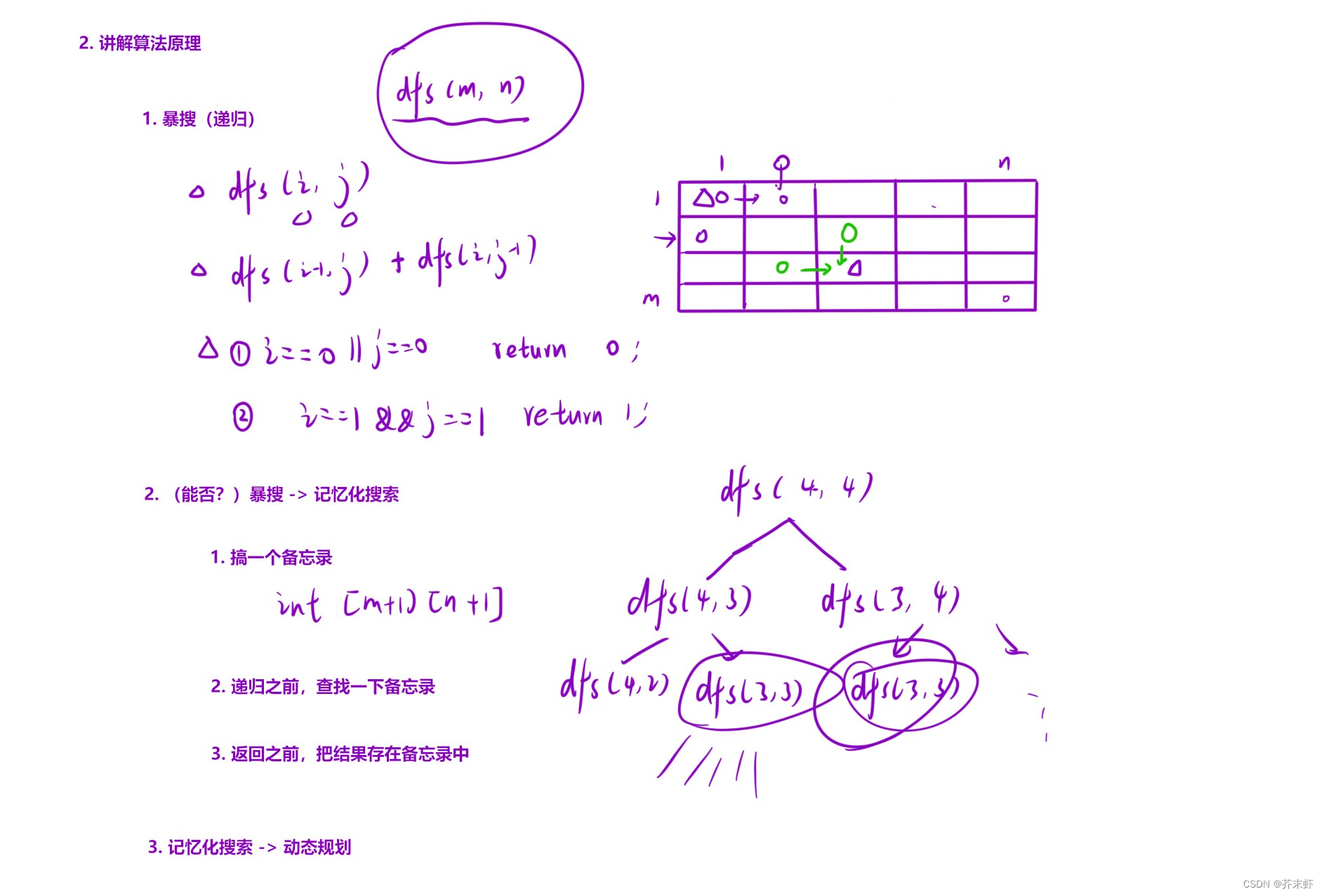
动态规划:从(1, 1)位置走起,到(m, n)位置结束。将第0行,第0列空下初始化为0方便处理边界情况。
编写代码
//解法一:记忆化搜索——自顶向下
class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>> memo(m+1, vector<int>(n+1, 0));return dfs(m, n, memo);}int dfs(int m, int n, vector<vector<int>>& memo){if(m<1 || n<1) return 0;if(m==1 && n==1) return 1;if(memo[m][n]!=0) return memo[m][n];memo[m][n] = dfs(m-1, n, memo)+dfs(m, n-1, memo);return memo[m][n];}
};//解法二:动态规划——自底向上
class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>> dp(m+1, vector<int>(n+1, 0));dp[1][1] = 1;for(int i = 1; i <= m; ++i){for(int j = 1; j <= n; ++j){if(i==1 && j==1) continue;else dp[i][j] = dp[i-1][j]+dp[i][j-1];}}return dp[m][n];}
};
2.2 最长递增子序列
题目链接
300. 最长递增子序列 - 力扣(LeetCode)
题目描述

算法原理
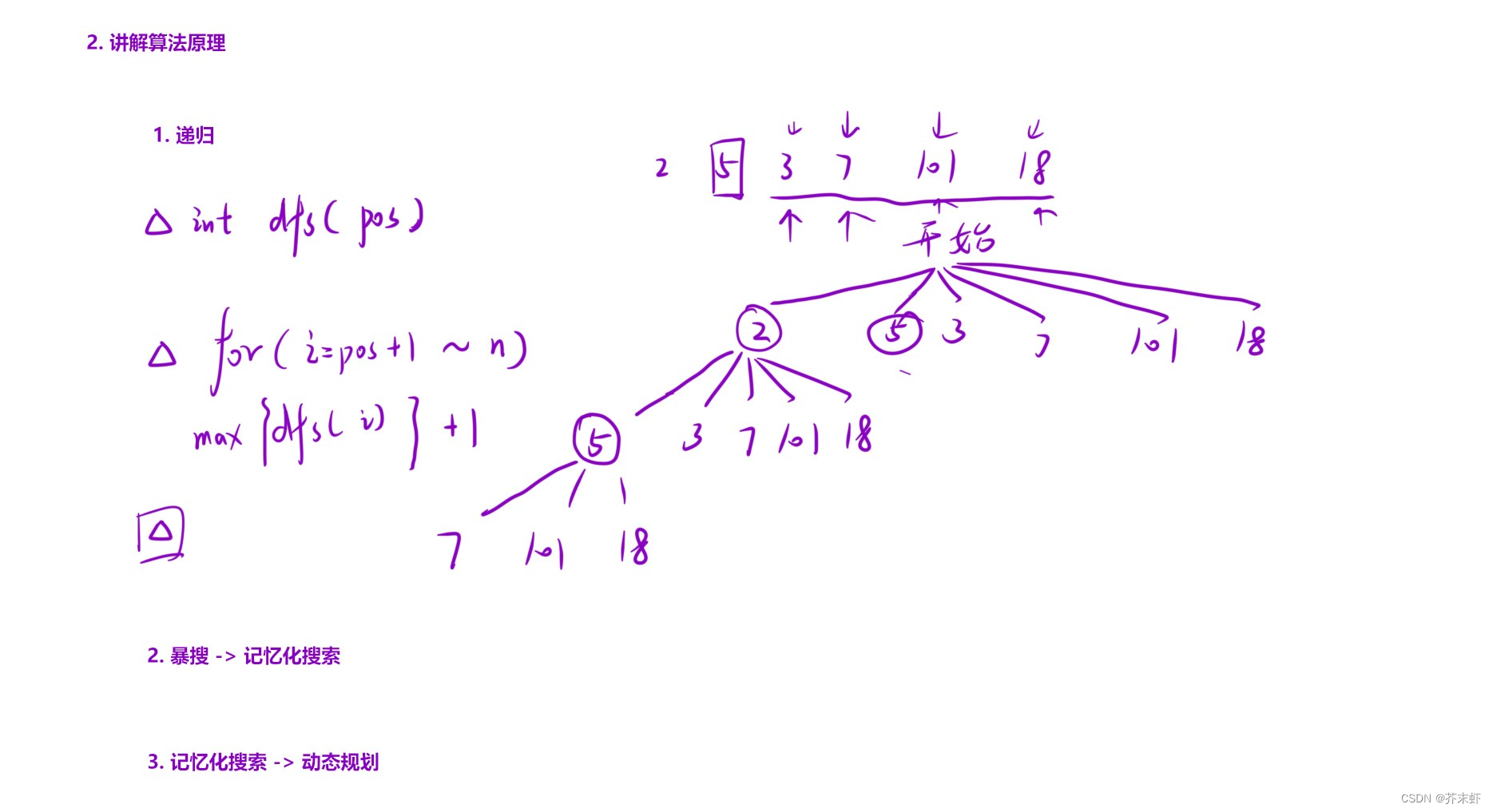
编写代码
//解法一:记忆化搜索——自顶向下
class Solution {int n;
public:int lengthOfLIS(vector<int>& nums) {n = nums.size();vector<int> memo(n, 0); //记录的是每个位置对应的最长递增子序列int ret = 1;for(int i = 0; i < n; ++i) //选择子序列的首元素{ret = max(ret, DFS(nums, i, memo));}return ret;}int DFS(vector<int>& nums, int pos, vector<int>& memo){if(memo[pos] != 0) return memo[pos];int ret = 1; //这里一定要初始化为1,最后一个元素不进入循环直接返回1for(int i = pos+1; i < n; ++i){if(nums[i] > nums[pos]) //要满足递增的要求{ret = max(ret, DFS(nums, i, memo)+1);}}memo[pos] = ret;return ret;}
};//解法二:动态规划——自底向上
class Solution {
public:int lengthOfLIS(vector<int>& nums) {int n = nums.size();vector<int> dp(n, 1);dp[n-1] = 1; //初始化:最后一个位置的长度为1int ret = 1;for(int i = n-1; i >= 0; --i) //填表顺序:从右向左{for(int j = i+1; j < n; ++j) //状态转移方程{if(nums[j] > nums[i])dp[i] = max(dp[i], dp[j]+1);}ret = max(ret, dp[i]);}return ret;}
};
2.3 猜数字大小Ⅱ
题目链接
375. 猜数字大小 II - 力扣(LeetCode)
题目描述
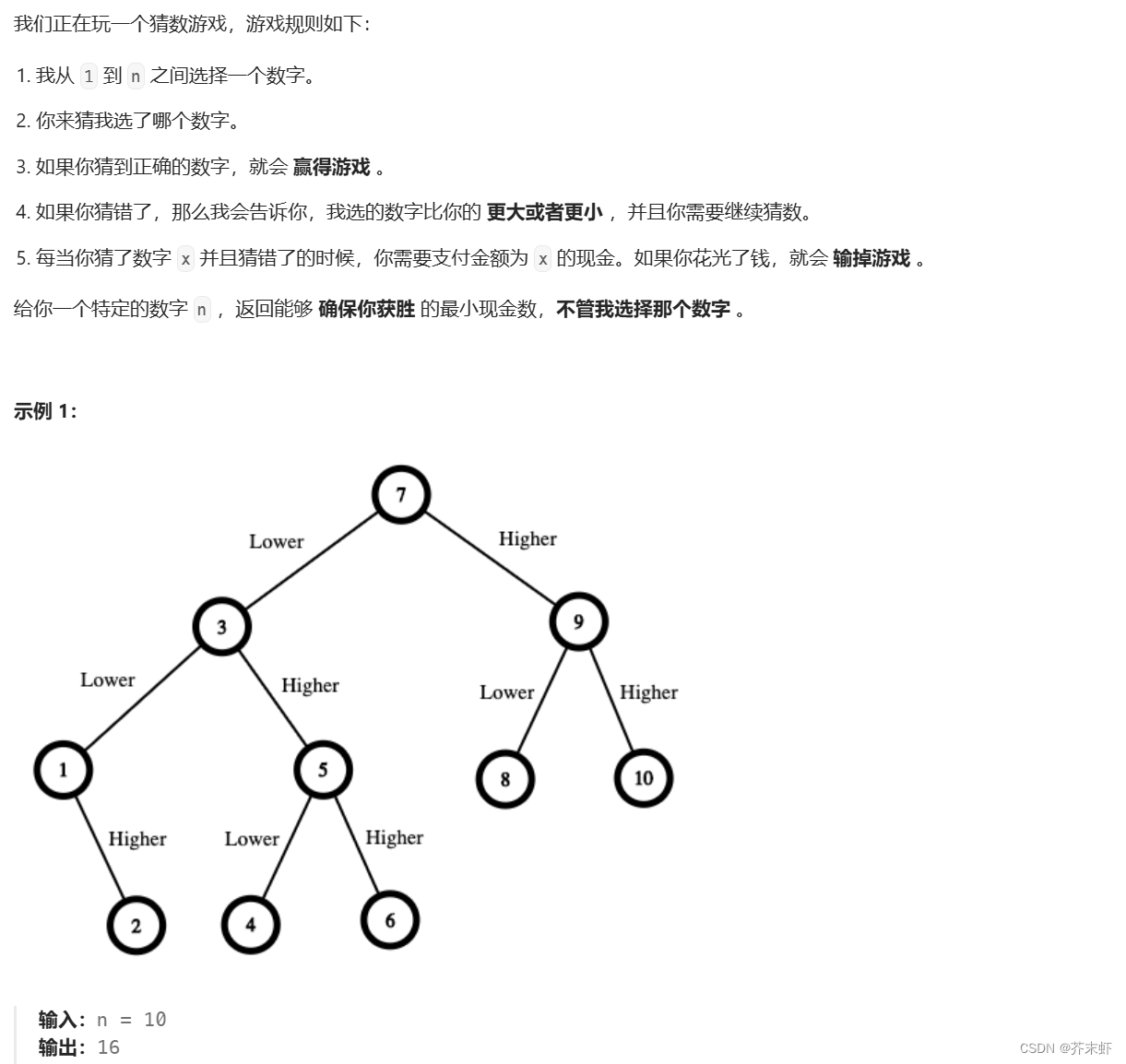
算法原理
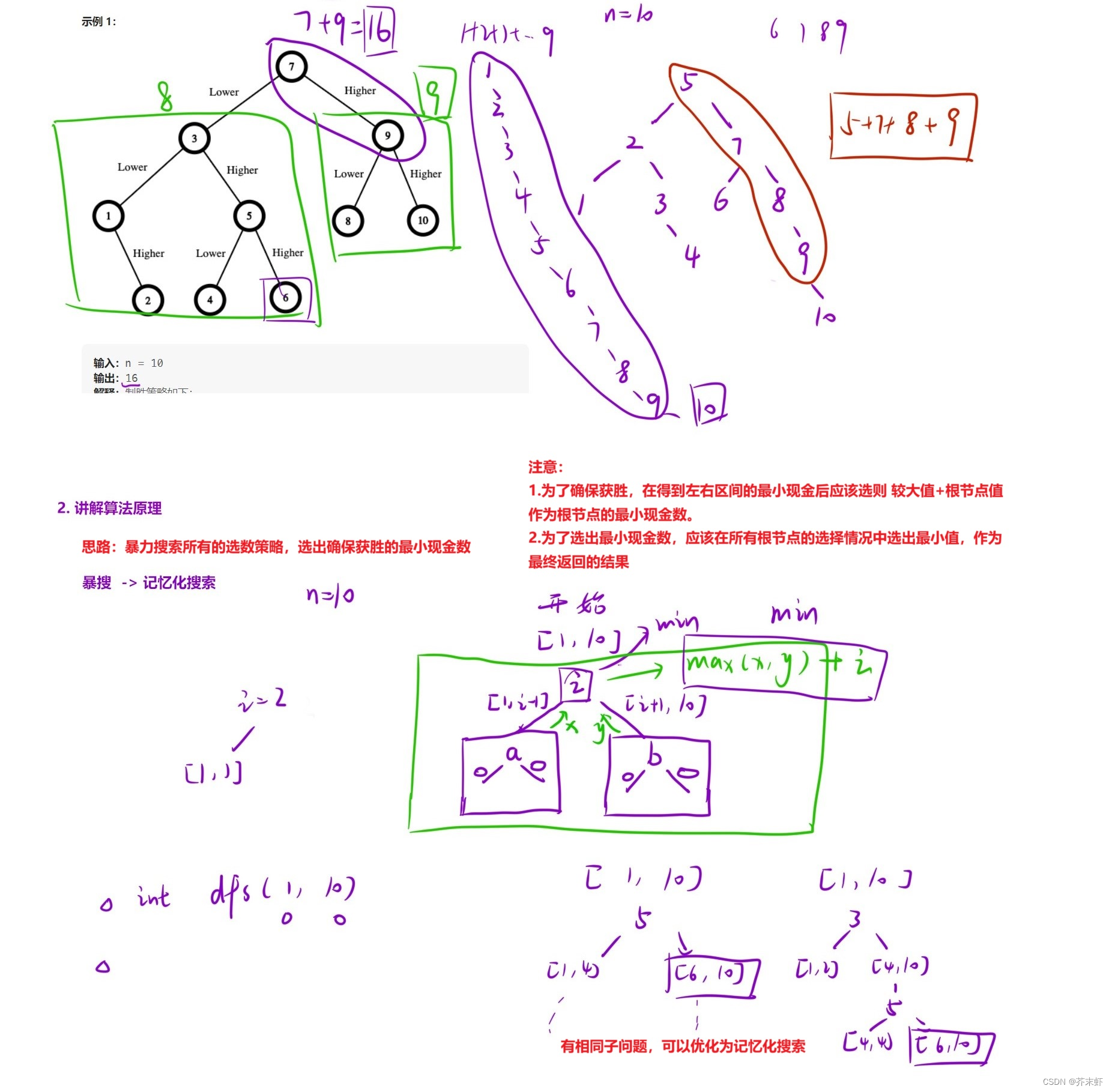
编写代码
class Solution {
public:int getMoneyAmount(int n) {vector<vector<int>> memo(n+1, vector<int>(n+1, 0)); //memo记录的是i位置的最小现金return DFS(1, n, memo); //DFS返回的是确保获胜的最小现金数}int DFS(int l, int r, vector<vector<int>>& memo){if(l >= r) return 0; //l>r区间不存在;l==r区间内只有一个元素,一次选中不需要付钱if(memo[l][r] != 0) return memo[l][r];int ret = INT_MAX;for(int i = l; i <= r; ++i){int left = DFS(l, i-1, memo); //左区间int right = DFS(i+1, r, memo); //右区间int tmp = max(left, right)+i; //确保获胜取maxret = min(ret, tmp); //最小现金数取min}memo[l][r] = ret;return ret;}
};
2.4 矩阵中的最长递增路径
题目链接
329. 矩阵中的最长递增路径 - 力扣(LeetCode)
题目描述
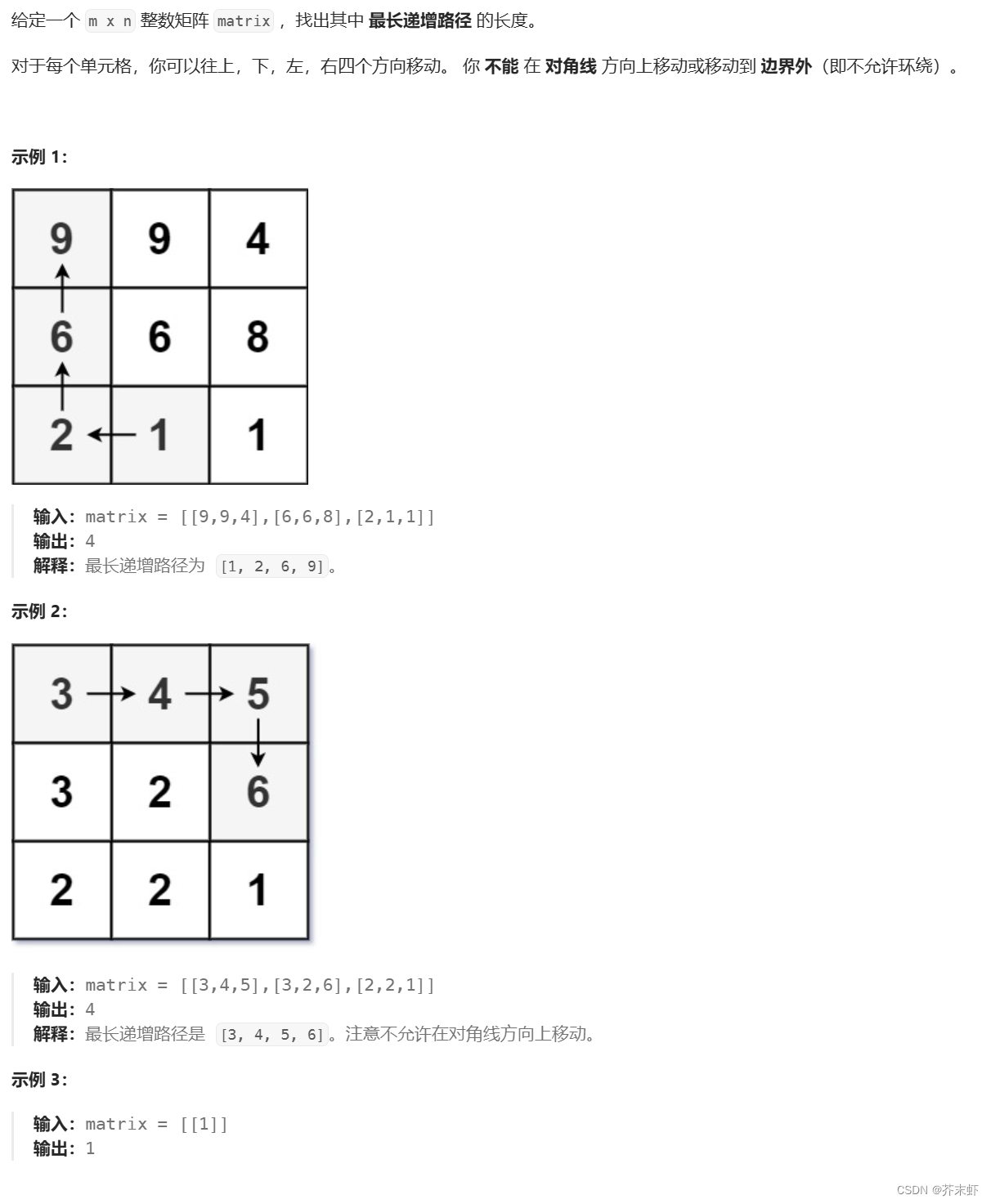
算法原理
见代码
编写代码
class Solution {int dx[4] = {0, 0, 1, -1};int dy[4] = {1, -1, 0, 0};int m, n;
public:int longestIncreasingPath(vector<vector<int>>& matrix) {m = matrix.size(), n = matrix[0].size();vector<vector<int>> memo(m, vector<int>(n, 0));int ret = 0;// 选择路径起点for(int i = 0; i < m; ++i){for(int j = 0; j < n; ++j){ret = max(DFS(matrix, i, j, memo), ret); //DFS暴搜+memo优化}}return ret;}int DFS(vector<vector<int>>& matrix, int r, int c, vector<vector<int>>& memo){if(memo[r][c] != 0) return memo[r][c];int ret = 1;for(int i = 0; i < 4; ++i){int x = r+dx[i], y = c+dy[i];if(x>=0 && x<m && y>=0 && y<n && matrix[x][y]>matrix[r][c]){ret = max(DFS(matrix, x, y, memo)+1, ret);}}memo[r][c] = ret;return ret;}
};
这篇关于【递归、搜索与回溯】记忆化搜索的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




