本文主要是介绍《检索技术核心20讲》进阶篇之LSM树,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
背景
学习极客实践课程《检索技术核心20讲》https://time.geekbang.org/column/article/215243,文档形式记录笔记。
内容
磁盘和内存数据读取特点
工业界中数据量往往很庞大,比如数据无法全部加载进内存,无法支持索引的高效实时更新,因此对于复杂的业务问题和业务场景,往往需要检索技术进行组合和升级。
内存称为随机访问存储器,只要给出内存地址就能直接访问数据。
磁盘是机械器件,访问数据的时候需要磁盘篇转到磁头下面,尽管磁盘旋转速度很快,但是和内存随机访问相比,一般来说会是10万到100万倍左右,但如果是顺序访问大批量数据的话,磁盘的性能和内存就是一个数量级的。
为何磁盘顺序读写比较快?磁盘的最小读写单位是扇区,较早期的磁盘的一个扇区是512字节,随着发展,目前常见的磁盘扇区是4K个字节,OS一次会读写多个扇区,所以OS的最小读写单位是块Block,也叫做簇Cluster,顺序读取磁盘这样OS就能一次读取多个块,这样相对下来效率会比较高。
PS:SSD硬盘和内存读写效率
- 以机械硬盘举例,顺序读写比随机读写少了多次 seek 的时间。 HDD 的 seek 耗时是 10ms ,吞吐率是 100MB/s,也就是每秒能 write 100MB 的数据。 那么以 1KB 为单位,纯写入1KB数据只需要 10us ,是seek 的 1/1000。
- SSD在seek时间上比HDD要快很多,但是SSD的工作原理如下:SSD最高层是 NAND Flash,每个 NAND Flash 里有多个 Block ,Block 里又包括很多 Page,SSD 的特点就是读和写都要以 Page 为单位,最少一个 Page。通常一个 Page 是 4k 或 8k。顺序读写只涉及到一个Page,随机读写涉及到多个Page,造成读写放大。
SSD是以page作为读写单位,以block作为垃圾回收单位,因此,批量顺序写性能依然大幅高于随机写!SSD的性能和内存相比依然有差距,因此,先在内存处理好,再批量写入SSD依然是高效的。
索引和数据分离之B+Tree
对磁盘的访问次数要尽可能少,假如使用一个数组存储信息到磁盘,这个大数组需要占用很多块,在查找的过程中,就需要多次加载块到内存进行二分查找,直到查询结束,这样一次查询可能需要访问很多次磁盘,这种情况应该尽量避免。索引和数据文件分离是一种常见的设计思路,B+Tree就是这莫设计的。
索引和数据文件分离就是假如需要存储的内容比较多,那么得放入磁盘,但是全部字段放入的话查询需要访问很多次磁盘,效率比较低,因此可以拆分一个索引文件,索引文件只存储数据项的唯一标识以及指向磁盘数据的指针,这样索引文件会小很多,某些情况下可以加载进内存进行查询。
这种称为线性索引,对于更新频繁的场景,有序数据并不是一个很好的选择,删除数据,更新数据的话需要进行索引调整,而数组是连续的内存空间,二叉树和Hash索引往往更具有普适性,但是Hash索引又不支持范围查询,因此使用二叉树做索引比较合适。
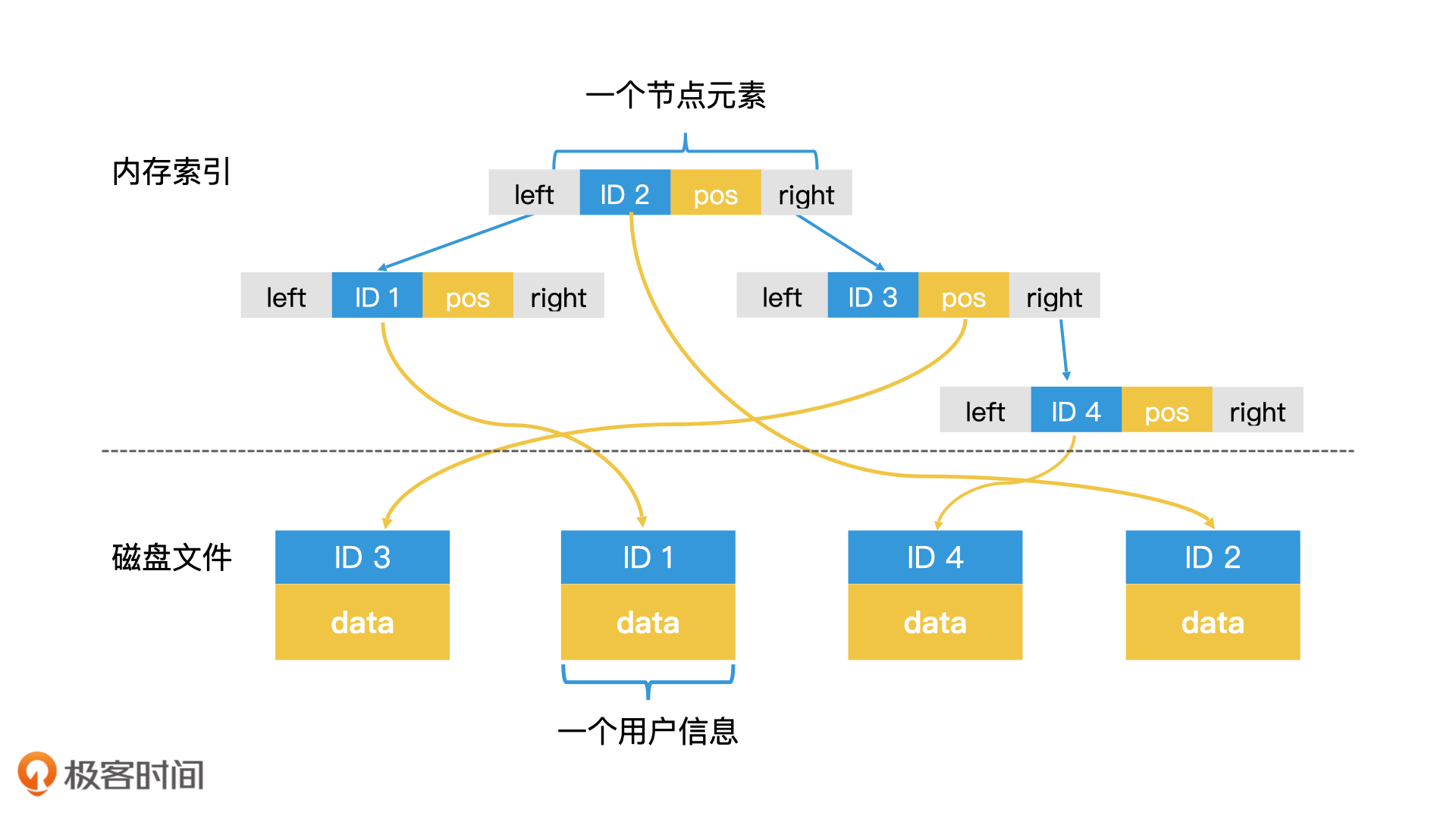
B+ Tree结构
B+ 树给出了将树形索引的所有节点都存在磁盘上的高效检索方案,使得索引技术摆脱了内存空间的限制,得到了广泛的应用。
B+ 树是一棵完全平衡的 m 阶多叉树。所谓的 m 阶,指的是每个节点最多有 m 个子节点,并且每个节点里都存了一个紧凑的可包含 m 个元素的数组。
B+树的一个关键设计就是节点的数据大小和OS块大小一致,这样可以提高磁盘的读取效率,节点存储的元素不是一个元素,而是m个元素的有序数组。
B+树的另外一个关键设计就是所有节点分为叶子节点、非叶子节点,结构是一样的,但是存储的内容是不同的。非叶子节点存储key以及树形结构的指针,而不是数据的指针,这样可以使用更少的节点组织数据。叶子节点可以存储指针 or 数据,像MySQL中的innoDB就是存储的数据,MyISAM存储的就是指针。
另外B+树还讲同一层的所有节点做成有序的双链表,这样可以进行很好的范围查询以及灵活调整能力。
B+ 树的一个节点就能存储一个包含 m 个元素的数组,这样的话,一个只有 2 到 4 层的 B+ 树,就能索引数量级非常大的数据了,因此 B+ 树的层数往往很矮。比如说,一个 4K 的节点的内部可以存储 400 个元素,那么一个 4 层的 B+ 树最多能存储 400^4,也就是 256 亿个元素。
另外可以前几层的节点数据加载到内存中做缓存,进一步减少索引文件磁盘访问次数。比如说,对于一个 4 层的 B+ 树,每个节点大小为 4K,那么第一层根节点就是 4K,第二层最多有 400 个节点,一共就是 1.6M;第三层最多有 400^2,也就是 160000 个节点,一共就是 640M。对于现在常见的计算机来说,前三层的内部节点其实都可以存储在内存中,只有第四层的叶子节点才需要存储在磁盘中。这样一来,我们就只需要读取一次磁盘即可。这也是为什么,B+ 树要将内部节点和叶子节点区分开的原因。通过这种只让内部节点存储索引数据的设计,我们就能更容易地把内部节点全部加载到内存中了。
B+Tree动态调整
插入删除元素,节点调整,比如以一个m=3的B+树需要插入ID=6的这个记录,首先需要二分查找到叶子节点,叶子节点未满的话,直接插入就行。
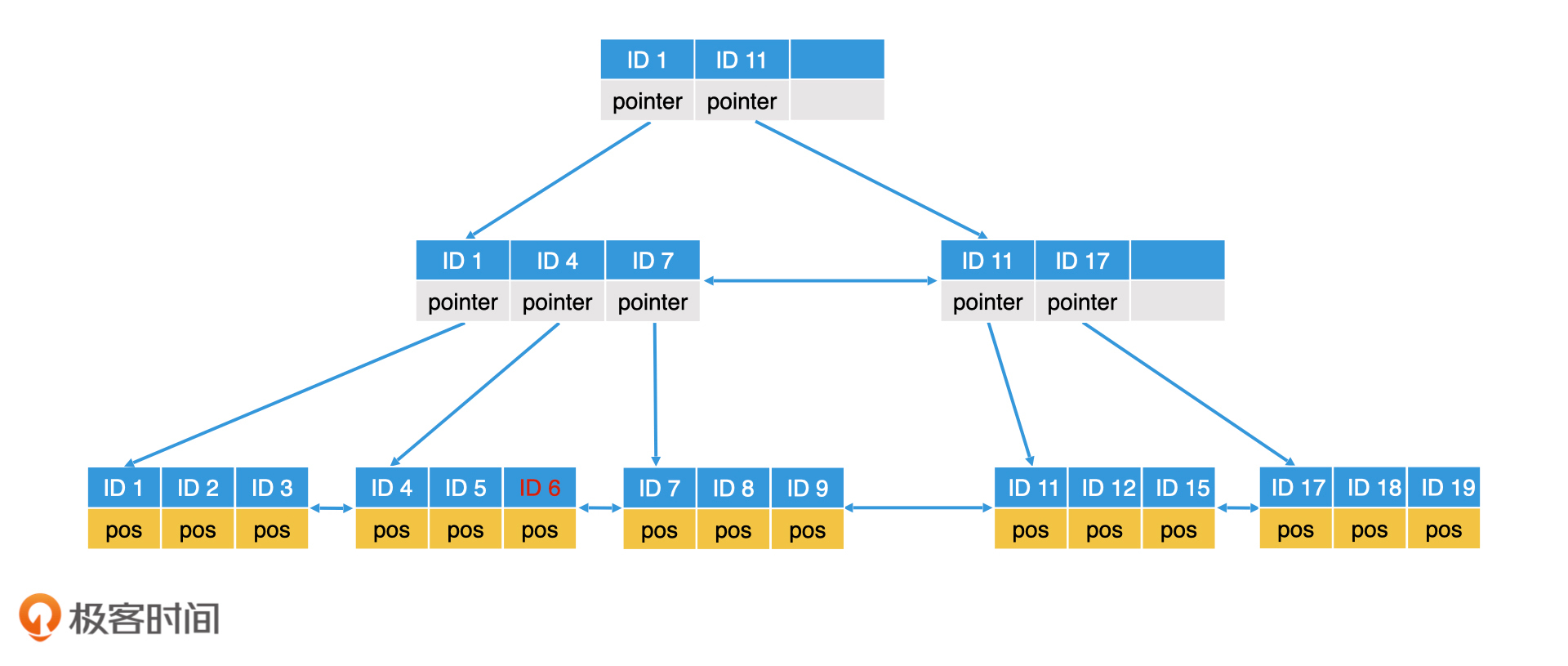
叶子节点满了的话需要进行叶子节点块分裂,比如插入ID=10的记录,就要进行分裂,逻辑就是生成一个新的节点,然后讲数据平分。叶子节点分裂完成以后,上一层的内部节点也需要修改。但如果上一层的父节点也是满的,那么上一层的父节点也需要分裂。
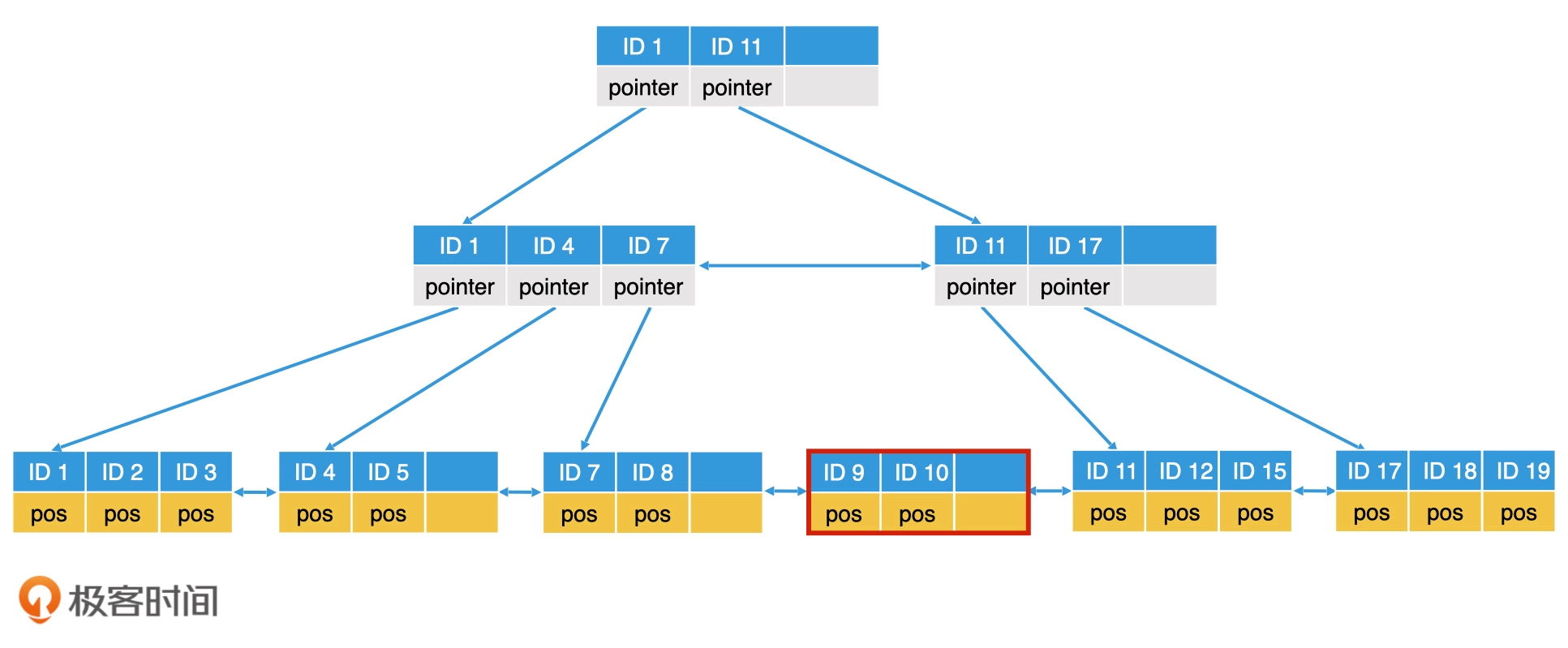
删除也需要动态调整节点,也需要进行判断,如果从一个元素已经满的叶子节点删除一个元素,直接删除即可。如果一个叶子节点删除某个元素后,有一半以上的空间为空,就需要移动兄弟的节点,可以成功转移的条件是,元素转移后该节点及其兄弟节点的空间必须都能维持在半满以上。如果无法满足这个条件,就说明兄弟节点其实也足够空闲,那我们直接将该节点的元素并入兄弟节点,然后删除该节点即可。
思考1:B+树的一个很大优势就是适合做范围查询。如果我们要检索值在 x 到 y 之间的所有元素,你会怎么操作呢?想到就是找出x值所在的节点,然后沿着叶子节点向后找直到找到y。这里需要注意B+树的叶子节点块之间也不是连续存储的,采用两次二分就不太适合了,不能将全部数据一次取出。
非关系型数据结构存储之LSM树
在关系型数据库之外,还有许多常见的大数据应用场景,比如,日志系统、监控系统。这些应用场景有一个共同的特点,那就是数据会持续地大量生成,而且相比于检索操作,它们的写入操作会非常频繁。另外,即使是检索操作,往往也不是全范围的随机检索,更多的是针对近期数据的检索。
如果是一个日志系统,每秒钟要写入上千条甚至上万条数据,使用B+树随机写入这样的磁盘操作代价会使得系统性能急剧下降,甚至无法使用。一种常见的设计思路和检索技术:LSM 树(Log Structured Merge Trees)。LSM 树也是近年来许多火热的 NoSQL 数据库中使用的检索技术。
LSM的设计思路
针对B+树随机写入慢的特点,可以考虑将数据按照 block块 写入,可以大幅减少写入次数。
LSM树就是根据这个思路设计的,**批量写入以批量顺序写入磁盘减少随机写入次数 **,先将数据放入内存的树中,积攒到一定量在写入磁盘,当数据写入时,延迟写磁盘,将数据先存放在内存中的树里,进行常规的存储和查询。当内存中的树持续变大达到阈值时,再批量地以块为单位写入磁盘的树中。
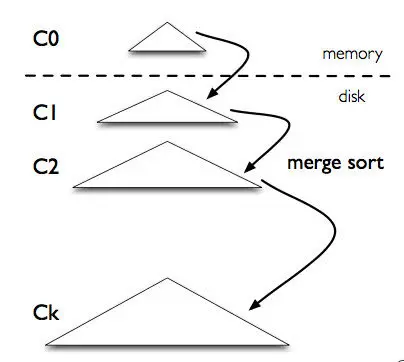
图源:https://zhuanlan.zhihu.com/p/415799237
LSM的结构是一个森林,类似BKD-Tree,可以分为内存树、磁盘树,
- 至于磁盘树,可以使用类似B+树实现,按照Block写入效率比较高磁盘树是一棵满二叉树(其实是一个SSTable结构,存储kv结构,为了好理解可以理解为B+树),也就是叶子节点都是满的。
- 对于内存树,结构可以使用AVL、跳表等实现。数据首先写入到内存树,满了之后刷到磁盘中,在内存中的数据支持更快的检索和修改。
LSM的结构

主要有三部分组成:
- _MemTable:_MemTable是在**内存**中的数据结构,用于保存最近更新的数据,会按照Key有序地组织这些数据,LSM树对于具体如何组织有序地组织数据并没有明确的数据结构定义,例如Hbase使跳跃表来保证内存中key的有序。因为数据暂时保存在内存中,内存并不是可靠存储,如果断电会丢失数据,因此通常会通过WAL(Write-ahead logging,预写式日志)的方式来保证数据的可靠性。
- _Immutable MemTable:_当 MemTable达到一定大小后,会转化成Immutable MemTable。Immutable MemTable是将转MemTable变为SSTable的一种中间状态。写操作由新的MemTable处理,在转存过程中不阻塞数据更新操作。
- _SSTable(Sorted String Table):磁盘树可以有很多层,每层可以有多个SSTable,有序键值对_集合,是LSM树组在**磁盘**中的数据结构。为了加快SSTable的读取,可以通过建立key的索引以及布隆过滤器来加快key的查找。一个key可以存在不同level的的不同SSTable中,但是上一层的level的key新鲜度总是高于下层的,同一层中的多个SSTable只能有一个key。

LSM的崩溃恢复
内存树的数据断电易丢失,LSM使用WAL(预写日志技术)来保证数据不丢失,在写入数据到内存的时候快速的写入日志到磁盘,具体步骤
- 内存中的程序在处理数据时,会先将对数据的修改作为一条记录,顺序写入磁盘的 log 文件作为备份。由于磁盘文件的顺序追加写入效率很高,因此许多应用场景都可以接受这种备份处理。
- 在数据写入 log 文件后,备份就成功了。接下来,该数据就可以长期驻留在内存中了。
- 系统会周期性地检查内存中的数据是否都被处理完了(比如,被删除或者写入磁盘),并且生成对应的检查点(Check Point)记录在磁盘中。然后,我们就可以随时删除被处理完的数据了。这样一来,log 文件就不会无限增长了。
- 系统崩溃重启,我们只需要从磁盘中读取检查点,就能知道最后一次成功处理的数据在 log 文件中的位置。接下来,我们就可以把这个位置之后未被处理的数据,从 log 文件中读出,然后重新加载到内存中。
通过这种预先将数据写入 log 文件备份,并在处理完成后生成检查点的机制,可以安全的使用内存来检索、存储数据了。
LSM的数据合并思路
内存树被写满之后,需要将数据合并到磁盘中的树中,称之为滚动合并(Rolling Merge)。
便于理解,同样磁盘树理解为B+树,参考链表的归并排序,将内存树和磁盘树的数据读取出来,放入内存进行归并,需要注意的是为了提高磁盘树的读写效率,对于磁盘树除了根节点外的节点,尽可能放入连续的块中,这样可以按块加载多个相邻的数据节点,这样的块叫做 多页块(Multi-Pages Block)。
合并步骤
- 第一步,以多页块为单位,将 C1 树的当前叶子节点从前往后读入内存。读入内存的叫作清空块(Emptying Block),意思是处理完以后会被清空。
- 第二步,将 C0 树的叶子节点和清空块中的数据进行归并排序,把归并的结果写入内存的一个新块中,叫作填充块(Filling Block)。
- 第三步,如果填充块写满了,我们就要将填充块作为新的叶节点集合顺序写入磁盘。这个时候,如果 C0 树的叶子节点和清空块都没有遍历完,我们就继续遍历归并,将数据写入新的填充块。如果清空块遍历完了但是C1叶子节点还没遍历完,我们就去 C1 树中顺序读取新的多页块,加载到清空块中。
- 第四步,重复第三步,直到遍历完 C0 树和 C1 树的所有叶子节点,并将所有的归并结果写入到磁盘。这个时候,我们就可以同时删除 C0 树和 C1 树中被处理过的叶子节点。
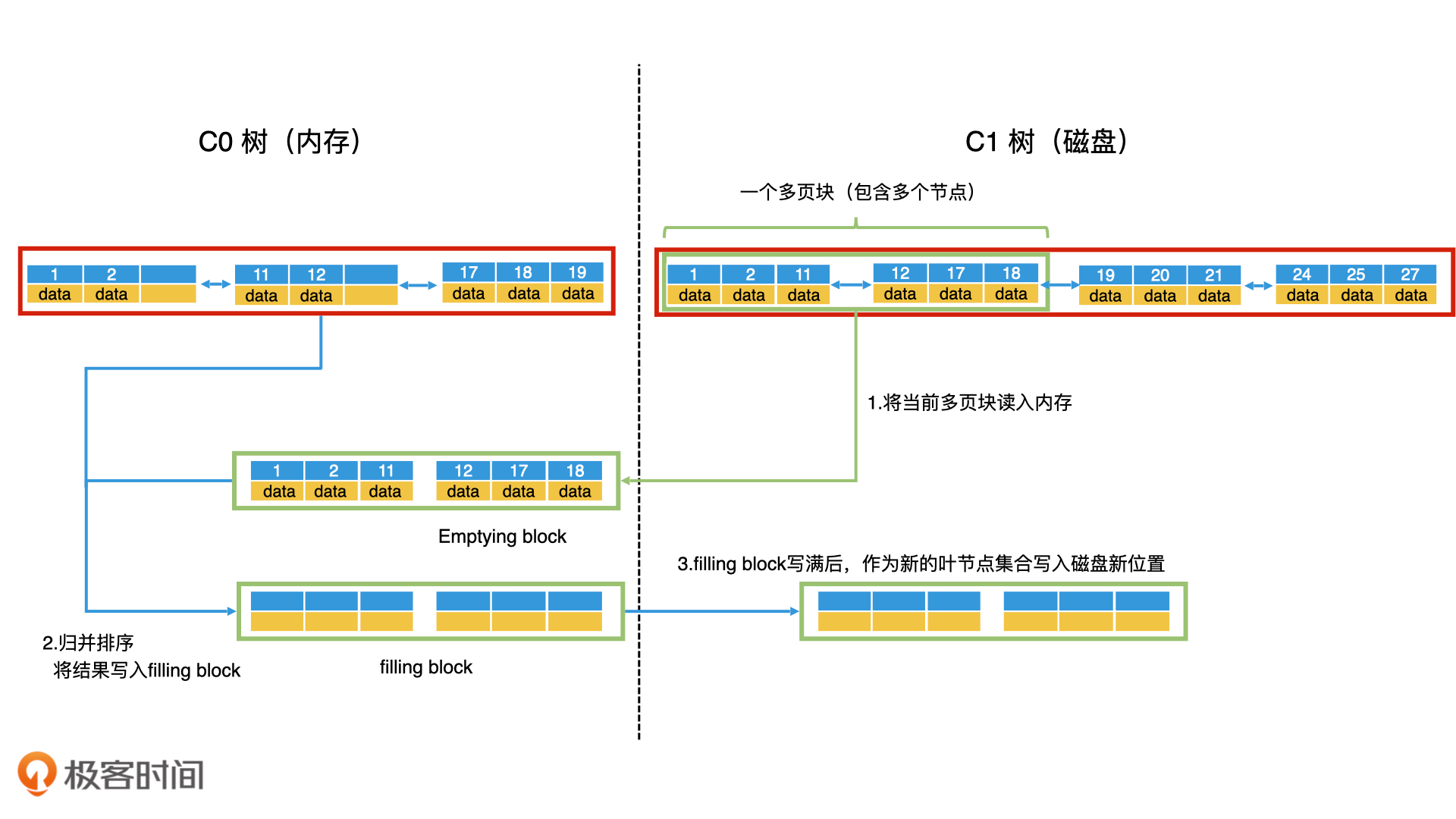
这样就完成了滚动归并的过程。在 C0 树到 C1 树的滚动归并过程中,你会看到,几乎所有的读写操作都是以多页块为单位,将多个叶子节点进行顺序读写的。而且,因为磁盘的顺序读写性能和内存是一个数量级的,这使得 LSM 树的性能得到了大幅的提升。
LSM树的检索之删除标记
先查内存树,如果内存有,直接作为结果返回,内存中的数据是最新的。
如果内存树没有,查询磁盘树,先以单棵B+树为例,这时候查到数据需要检查数据的时效性,因为LSM批量写入的特点,可能存在磁盘脏数据问题。
如一个数据已经被写入系统了,并且我们也把它写入 C1 树了。但是,在最新的操作中,这个数据被删除了,那我们自然不会在 C0 树中查询到这个数据。可是它依然存在于 C1 树之中。LSM解决办法是依然采用延迟写入,尽量避免随机访问磁盘树,对于被删除的数据,同样将这个数据key插入到内存树,只不过key上加了删除标志。
这样一来,当我们在 C0 树中查询时,如果查到了一个带着删除标志的 key,就直接返回查询失败,我们也就不用去查询 C1 树了。在滚动归并的时候,我们会查看数据在 C0 树中是否带有删除标志。如果有,滚动归并时就将它放弃。这样 C1 树就能批量完成“数据删除”的动作。
LSM树的两种合并策略
合并时机
- 因为内存不是无限大,Level 0树达到阈值时,需要将数据从内存刷到磁盘中,这是合并操作的第一个场景;
- 需要对磁盘上达到阈值的顺序文件进行归并,并将归并结果写入下一层,归并过程中会清理重复的数据和被删除的数据(墓碑标记)。我们分别对上述两个场景进行分析:
为了防止SSTable的数量不断增加,合并策略很关键,主要介绍两种基本策略:size-tiered和leveled
- size-tiered 策略:size-tiered策略保证每层SSTable的大小相近,同时限制每一层SSTable的数量。如上图,每层限制SSTable为N,当每层SSTable达到N后,则触发Compact操作合并这些SSTable,并将合并后的结果写入到下一层成为一个更大的sstable。由此可以看出,当层数达到一定数量时,最底层的单个SSTable的大小会变得非常大。并且size-tiered策略会导致空间放大比较严重**。**即使对于同一层的SSTable,每个key的记录是可能存在多份的,只有当该层的SSTable执行compact操作才会消除这些key的冗余记录。
- leveled策略:限制每一层的SSTable总文件大小。

LSM的检索
如果内存树没有,查询磁盘树,以SSTable为例,先查level1的多个SSTable,没有就查level2的,一次类推,如果在level2的SSTabel都找到了key,就返回结果。
综上我们可以给出LSM树的优缺点:
- 优:增、删、改操作飞快,写吞吐量极大。
- 缺:对于SSTable实现的磁盘树,读操作性能相对被弱化;不擅长区间范围的读操作; 归并操作较耗费资源。
如果说B/B+树的读写性能基本平衡的话,LSM树的设计原则通过舍弃部分读性能,换取了无与伦比的写性能。该数据结构适合用于写吞吐量远远大于读吞吐量的场景,得到了NoSQL届的喜爱和好评。
思考:LSM磁盘树可以很多层,每层可有多个SSTable,多个SSTable不像单个B+树那样可以直接按照key查找值,而是一个key可以存在不同层的不同SSTable中(一层多个SSTable只能有一个相同key),这样查时间比较久的数据的时候如何保证找到最新的key以及值?一个key可以存在不同level中,但是上一层的level的key新鲜度总是高于下层的,同一层中多个SSTable只有一个key。
思考1:内存树可以使用什么结构?取决于应用场景,可以使用哈希表、红黑树、跳表等,比如需要范围扫描,可以使用跳表或者红黑树、AVL比较合适。
这篇关于《检索技术核心20讲》进阶篇之LSM树的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!