代码随想录算法训练营第二十四天| （回溯） 77. 组合、 216.组合总和III、17.电话号码的字母组合

本文主要是介绍代码随想录算法训练营第二十四天| （回溯） 77. 组合、 216.组合总和III、17.电话号码的字母组合，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

77. 组合

题目链接：77. 组合
文档讲解：代码随想录
状态：很多细节忘了

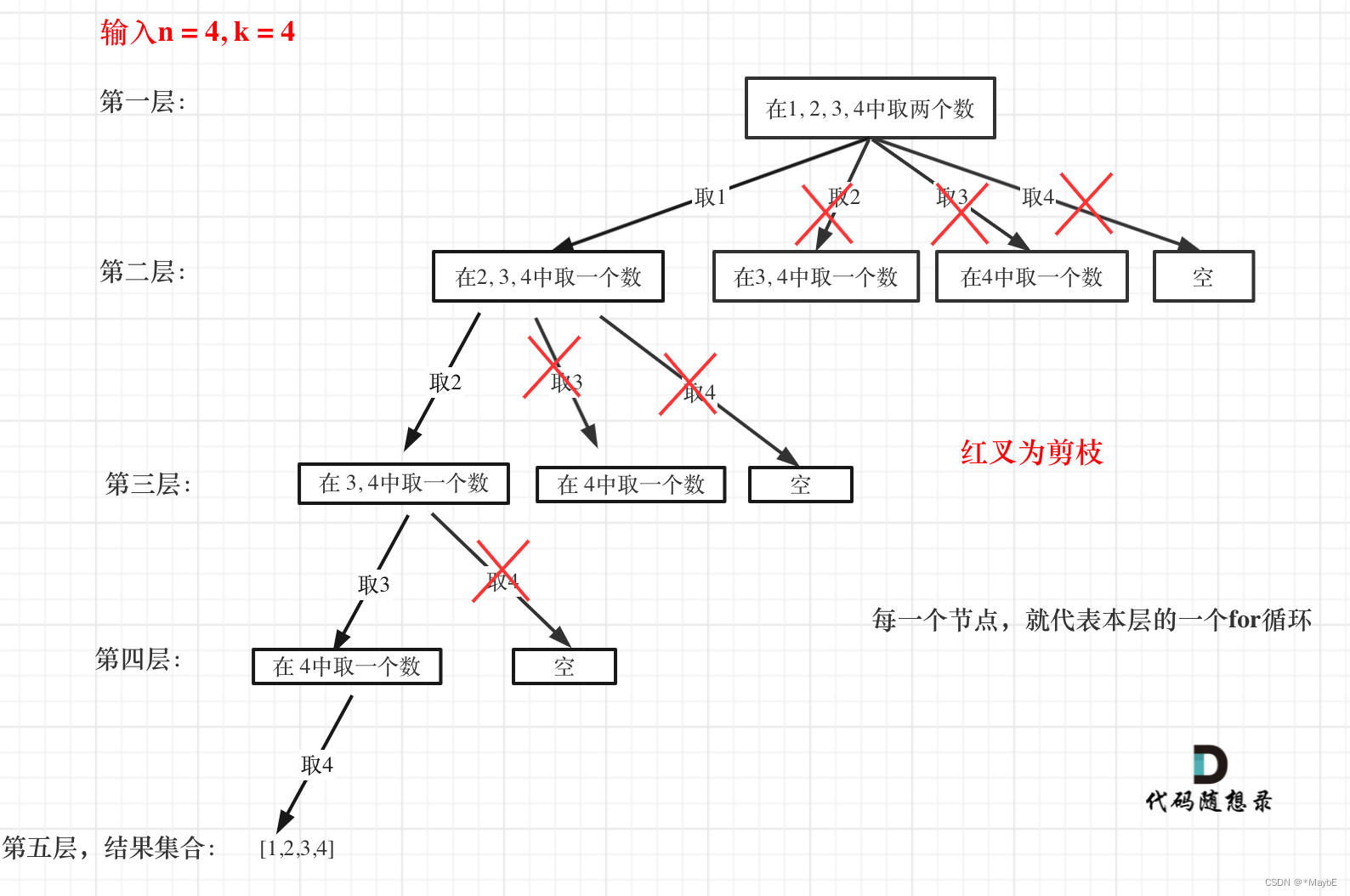
思路：先画图，然后可以发现，从1到n中选择k个数，可以看成是一个递归过程，这个递归的深度就是k。然后遍历当前这层集合可以看作一个for循环，就是逐个元素尝试的过程。

• for 循环：遍历集合的宽度，是一个取元素的过程。它负责在当前递归层次上，依次选择不同的元素，并将选择的元素添加到当前路径 path 中。
• backtracking 方法：组合的过程。它负责递归地处理后续的选择，构建出完整的组合。当路径 path 满足条件（长度等于 k）时，将当前路径添加到结果列表 res 中。

剪枝优化：画图时可以发现，有时for循环后面几个集合不满足条件可以提前结束。
这里剪枝有两种思路：

1. path.size()表示当前已经收集到的元素个数，k - path.size()表示还剩几个元素需要收集，n - (k - path.size()) + 1 表示当前位置 i 往后至少还需几个元素才能凑齐。如果 i 超过这个范围，就意味着即使选择当前位置的元素，剩余的元素数量也不足以凑齐需要选择的个数，因此就没有必要继续往下搜索了，可以提前结束这个分支的搜索。
2. 也可以这样理解：k-path.size()<=n-i+1,就是还需收集的元素的个数应该小于当前还能选的元素的个数。
   

错误代码：

    public void backtracking(int n, int k, List<List<Integer>> res, LinkedList<Integer> path) {if (path.size() == k) {res.add(path);//错误1.res每次应该加入的是新的path,因为path回溯的过程中会导致res中的path为空!return;}for (int i = 1; i <= n - k + 1; i++) {//错误2.i应该从start开始;错误3.剪枝操作应该是i<=n-(k-path.size())+1,path.add(i);backtracking(i + 1, k, res, path);//错误2.这里第一个参数n是不会变的,因此需要一个start表示开始索引path.removeLast();}}

题解：

    public List<List<Integer>> combine(int n, int k) {List<List<Integer>> res = new ArrayList<>();LinkedList<Integer> path = new LinkedList<>();backtracking(n, k, 1, res, path);return res;}public void backtracking(int n, int k, int start, List<List<Integer>> res, LinkedList<Integer> path) {if (path.size() == k) {res.add(new ArrayList<>(path));return;}// 剪枝,k-path.size()<=n-i+1,就是还需收集的元素的个数应该小于当前还能选的元素的个数for (int i = start; k - path.size() <= n - i + 1; i++) {path.add(i);backtracking(n, k, i + 1, res, path);path.removeLast();}}

216.组合总和III

题目链接：216.组合总和III
文档讲解：代码随想录
状态：经过上一题后，写法想起来了，但是自己在剪枝这边的写法并不是最优的

思路：就是组合的基础上加上了求和。

题解：

List<List<Integer>> res = new ArrayList<>();LinkedList<Integer> path = new LinkedList<>();int sum = 0;// 主方法，找到所有k个数的组合，其和为npublic List<List<Integer>> combinationSum3(int k, int n) {backtracking(k, n, 1);return res;}// 回溯方法public void backtracking(int k, int n, int startIndex) {// 当路径长度等于k时，检查当前路径上的数字和是否等于目标值nif (path.size() == k) {if (sum == n) {// 如果满足条件，添加当前路径到结果列表中res.add(new ArrayList<>(path));}return;}// 从startIndex开始遍历数字1到9//剪枝: 一方面,剩余收集的元素数量要小于等于当前集合中剩余元素数量,另一方面当前路径上的数字和加上当前数字要小于等于目标值nfor (int i = startIndex; i <= 9 && k - path.size() <= 9 - i + 1 && sum + i <= n; i++) {path.add(i); // 将当前数字i加入路径sum += i;    // 更新当前路径数字和backtracking(k, n, i + 1); // 递归调用，继续选择下一个数字sum -= i;    // 回溯，撤销选择path.removeLast(); // 回溯，撤销选择}}

17.电话号码的字母组合

题目链接：17.电话号码的字母组合
文档讲解：代码随想录
状态：还行

思路：先将数字对应的字符串存到map或者数组中，递归的时候根据深度取不同的字符串，for循环则是对当前层的字符串进行遍历。

题解：

    String[] letterMap = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};List<String> res = new ArrayList<>();StringBuilder sb = new StringBuilder();public List<String> letterCombinations(String digits) {if (digits.isEmpty()) {return res;}char[] chars = digits.toCharArray();String[] strings = new String[chars.length];for (int i = 0; i < chars.length; i++) {strings[i] = letterMap[chars[i] - '0'];}backtracking(strings, chars.length);return res;}public void backtracking(String[] strings, int k) {if (sb.length() == k) {res.add(sb.toString());return;}int len = sb.length();char[] chars = strings[len].toCharArray();for (int i = 0; i <= chars.length - 1; i++) {sb.append(chars[i]);backtracking(strings, k);sb.setLength(len);}}

这篇关于代码随想录算法训练营第二十四天| （回溯） 77. 组合、 216.组合总和III、17.电话号码的字母组合的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---