本文主要是介绍【因果推断python】36_断点回归2,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
RDD 估计
内核加权
RDD 估计
RDD 依赖的关键假设是阈值处潜在结果的平滑性。用比较正式地表述来说,当运行变量从右侧和左侧接近阈值时,潜在结果的极限应该是相同的。
如果这是真的,我们可以在阈值处找到因果关系
从其本身意义来说,这是一种局部平均干预效果(LATE),因为我们只能在阈值处知道它。在这种情况下,我们可以将 RDD 视为局部随机试验。对于那些处于阈值附近的人来说,干预可能会采取任何一种方式,有些人可能低于门槛,有些人则可能超过了门槛。在我们的示例中,在同一时间点,有些人刚刚超过 21 岁,有些人刚刚低于 21 岁。决定这一点的是某人是否在几天后出生,这是非常随机的。基于这个原因,RDD 提供了一个非常引人注目的因果故事。它不是 RCT 的黄金标准,但很接近。
现在,要估计阈值处的干预效果,我们需要做的就是估计上面公式中的两个极限值并进行比较。最简单的方法是运行线性回归

为了使其工作,我们将一个高于阈值的虚拟变量与运行变量进行交叉
本质上,这与在阈值之上拟合线性回归并在阈值之下拟合另一个线性回归相同。参数 是低于阈值的回归的截距,而
是高于阈值的回归的截距。
这就是将运行变量在阈值处取零的技巧发挥作用的地方。在这个预处理步骤之后,阈值变为零。这导致截距 成为阈值处的预测值,用于低于它的回归。换句话说,
。同理,
是上述结果的极限。威奇的意思是
下面的代码展示了当我们想估计在21 岁时饮酒对死亡造成的影响。
rdd_df = drinking.assign(threshold=(drinking["agecell"] > 0).astype(int))model = smf.wls("all~agecell*threshold", rdd_df).fit()model.summary().tables[1]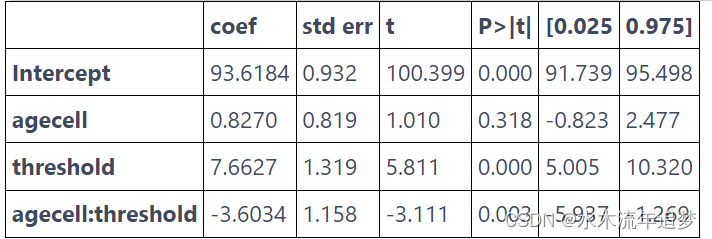
这个模型告诉我们,随着饮酒,死亡率会增加 7.6627 个百分点。 另一种说法是,酒精会使各种原因的死亡几率增加 8% ((7.6627+93.6184)/93.6184)。 请注意,这也为我们的因果效应估计提供了标准误差。 在这种情况下,效果具有统计显着性,因为 p 值低于 0.01。
如果我们想直观地验证这个模型,我们可以在我们拥有的数据上显示预测值。 您可以看到,就好像我们有 2 个回归模型:一个用于高于阈值的模型,一个用于低于阈值的模型。
ax = drinking.plot.scatter(x="agecell", y="all", color="C0")
drinking.assign(predictions=model.fittedvalues).plot(x="agecell", y="predictions", ax=ax, color="C1")
plt.title("Regression Discontinuity");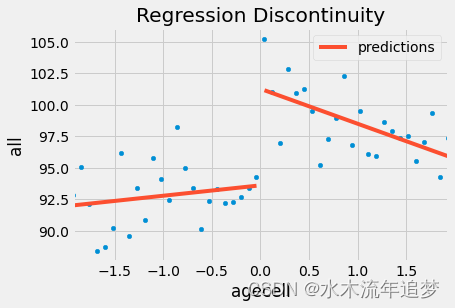
如果我们对其他原因做同样的事,这是我们会得到的结果。
plt.figure(figsize=(8,8))for p, cause in enumerate(["all", "mva", "suicide"], 1):ax = plt.subplot(3,1,p)drinking.plot.scatter(x="agecell", y=cause, ax=ax)m = smf.wls(f"{cause}~agecell*threshold", rdd_df).fit()ate_pct = 100*((m.params["threshold"] + m.params["Intercept"])/m.params["Intercept"] - 1)drinking.assign(predictions=m.fittedvalues).plot(x="agecell", y="predictions", ax=ax, color="C1")plt.title(f"Impact of Alcohol on Death: {np.round(ate_pct, 2)}%")plt.tight_layout()
RDD 告诉我们,酒精会使自杀和车祸死亡的几率增加 15%,这是一个相当大的数字。如果我们想尽量减少死亡率,这些结果是不降低饮酒年龄的有力论据。
内核加权
回归不连续性在很大程度上依赖于线性回归的外推特性。由于我们正在查看 2 条回归线的开头和结尾处的值,因此我们最好正确设置这些限制。可能发生的情况是,回归可能过于关注拟合其他数据点,而代价是在阈值处拟合不佳。如果发生这种情况,我们可能会得到错误的治疗效果衡量标准。
解决此问题的一种方法是为更接近阈值的点赋予更高的权重。有很多方法可以做到这一点,但一种流行的方法是使用 triangular kernel 重新加权样本
这个内核的第一部分是我们是否接近阈值的指示函数。多近?这由带宽参数 hℎ 确定。这个内核的第二部分是一个加权函数。随着我们远离阈值,权重变得越来越小。这些权重除以带宽。如果带宽很大,则权重会以较慢的速度变小。如果带宽很小,权重很快就会变为零。
为了更容易理解,下面是这个内核应用于我们的问题的权重。我在这里将带宽设置为 1,这意味着我们只会考虑来自不超过 22 岁且不低于 20 岁的人的数据。
def kernel(R, c, h):indicator = (np.abs(R-c) <= h).astype(float)return indicator * (1 - np.abs(R-c)/h)
plt.plot(drinking["agecell"], kernel(drinking["agecell"], c=0, h=1))
plt.xlabel("agecell")
plt.ylabel("Weight")
plt.title("Kernel Weight by Age");
如果我们将这些权重应用于我们最初的问题,酒精的影响会变得更大,至少对于死于"所有原因"的情况是如此。 它从 7.6627 跃升至 9.7004。 结果仍然非常显著。 另外,请注意我使用的是 wls 而不是 ols。
model = smf.wls("all~agecell*threshold", rdd_df,weights=kernel(drinking["agecell"], c=0, h=1)).fit()model.summary().tables[1]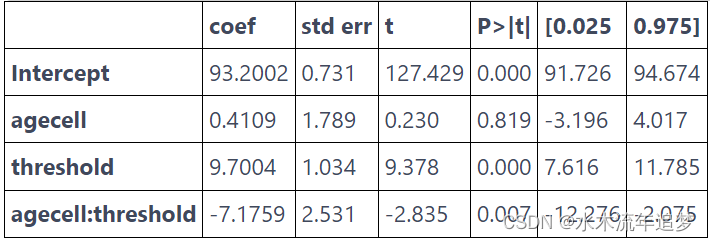
ax = drinking.plot.scatter(x="agecell", y="all", color="C0")
drinking.assign(predictions=model.fittedvalues).plot(x="agecell", y="predictions", ax=ax, color="C1")
plt.title("Regression Discontinuity (Local Regression)");
plt.figure(figsize=(8,8))
weights = kernel(drinking["agecell"], c=0, h=1)for p, cause in enumerate(["all", "mva", "suicide"], 1):ax = plt.subplot(3,1,p)drinking.plot.scatter(x="agecell", y=cause, ax=ax)m = smf.wls(f"{cause}~agecell*threshold", rdd_df, weights=weights).fit()ate_pct = 100*((m.params["threshold"] + m.params["Intercept"])/m.params["Intercept"] - 1)drinking.assign(predictions=m.fittedvalues).plot(x="agecell", y="predictions", ax=ax, color="C1")plt.title(f"Impact of Alcohol on Death: {np.round(ate_pct, 2)}%")plt.tight_layout()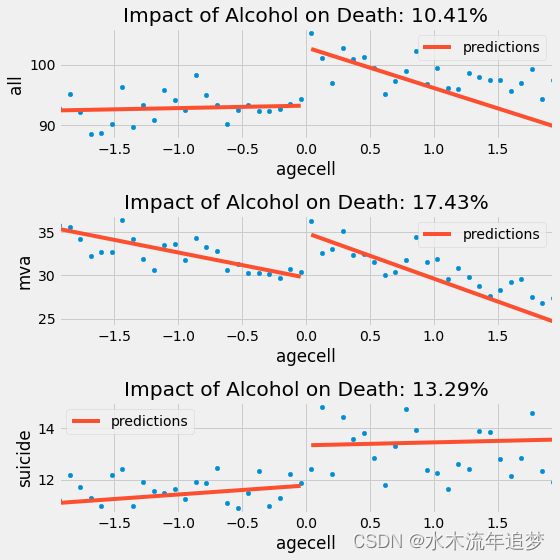
除了自杀之外,似乎使用核函数加权会使对酒精的负面影响更大。再同样的,如果我们想将死亡率降到最低,我们不应该建议降低法定饮酒年龄,因为酒精对死亡率有明显的影响。
这个简单的案例涵盖了当断点回归完美运行时会发生什么。接下来,我们将看到一些我们应该运行的诊断步骤,以检查我们对 RDD 的信任程度,并讨论一个我们非常关心的话题:教育对收入的影响。
这篇关于【因果推断python】36_断点回归2的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






