本文主要是介绍甄嬛传熹贵妃上户口：如果让他陪你过冬天，那朕能不能睡中间？贝叶斯模型推导爸爸去哪儿，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
关注微信公众号 数据分析螺丝钉 免费领取价值万元的python/java/商业分析/数据结构与算法学习资料
背景
《甄嬛传》是大家耳熟能详的宫廷剧，其中复杂的宫斗情节和深刻的人物刻画让人津津乐道。甄嬛因为与皇帝(四郎)闹翻了，去甘露寺待了一段时间，期间与云礼（王爷）谈恋爱，怀孕了，现在这四个人正商量怎么给孩子上户口，所以就有了皇帝出行甘露寺，与甄嬛见了一面，准备让皇帝接盘。
在皇帝封甄嬛为熹贵妃回宫后，被皇后一党找到甘露寺的蛛丝马迹，一上来就跟皇帝告发甄嬛，孩子不是皇帝的，皇帝顿时气不打一处来。
在这些错综复杂的关系中，四郎面临了一个巨大的困惑：如何确认孩子的真正父亲。在现代科学中，我们可以借助贝叶斯算法来解决这个问题。本文将通过四郎的视角，用贝叶斯算法推导出孩子是自己的概率。
一、问题
在宫廷中，怀疑孩子不是自己亲生的这种问题，直接的证据往往难以取得。而四郎手通过一次怀孕的概率、年龄对怀孕因素的影响、甄嬛见过的其他男性，我们可以建立一个贝叶斯模型来推导。
二、贝叶斯算法简介
贝叶斯算法是一种通过先验概率和似然函数来计算后验概率的统计方法。其公式如下：
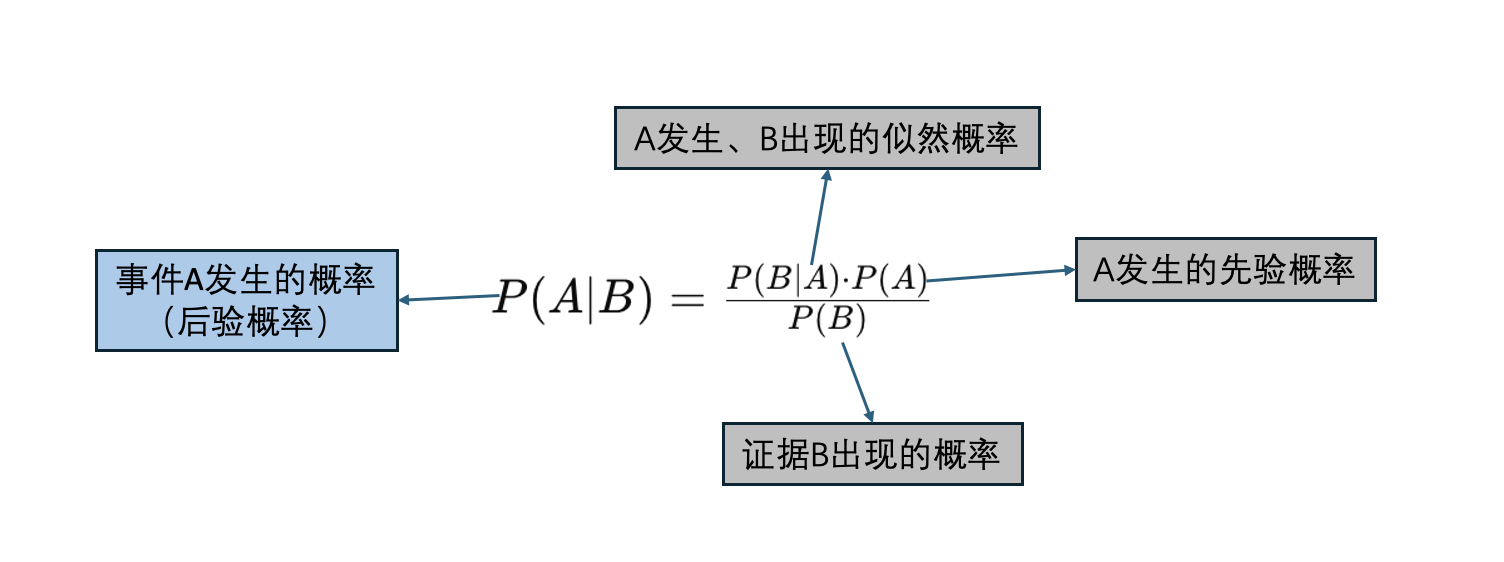
P(A）：所有可能是孩子父亲的男人们的概率
P(B)：收集到的线索在不同情况下会导致怀孕的概率
P(B|A) ：就是在A发生的情况下，B出现的普遍概率，比如 40岁的男人 怀孕概率小于30%，是经过验证测试调研，有大量数据证明的称为似然概率
P(A|B)： 在这些条件下，每个男人分别是孩子父亲的概率
三、设定假设
我们需要设定一些基本假设来应用贝叶斯公式，三位男候选人：
- A1：孩子是四郎亲生的。
- A2：孩子是果允礼亲生的。
- A3：孩子是温实初亲生的。
我们需要计算的目标是：孩子是四郎亲生的概率，即 ( P(A|B) )。
四、计算过程
-
先验概率 P(A1) ,P(A2) , P(A3).
根据给定的信息，虽然在甘露寺一段时间，先设置皇上概率更大一些，其他两个被发现了要被杀头，先验概率设定如下：
-
四郎的孩子：先验概率 ( P(A1) = 0.5 )
-
云礼的孩子：先验概率 ( P(A2) = 0.3 )
-
温实初的孩子：先验概率 ( P(A3) = 0.2 )
-
怀孕概率（似然函数） ( P(B|A1) ), ( P(B|A2) ), ( P(B|A3) )
似然函数考虑三方面的因素： -
年龄影响怀孕概率，根据学术期刊Science Direct的调研，不同人群的生育能力各有不同，无论男性还是女性，生育能力都会随着年龄的增长而下降
据统计，四郎47岁，云礼27岁 ，温实初27岁，甄嬛20岁，可以看到47岁能怀孕的概率最高10%，27岁 最高50%
-
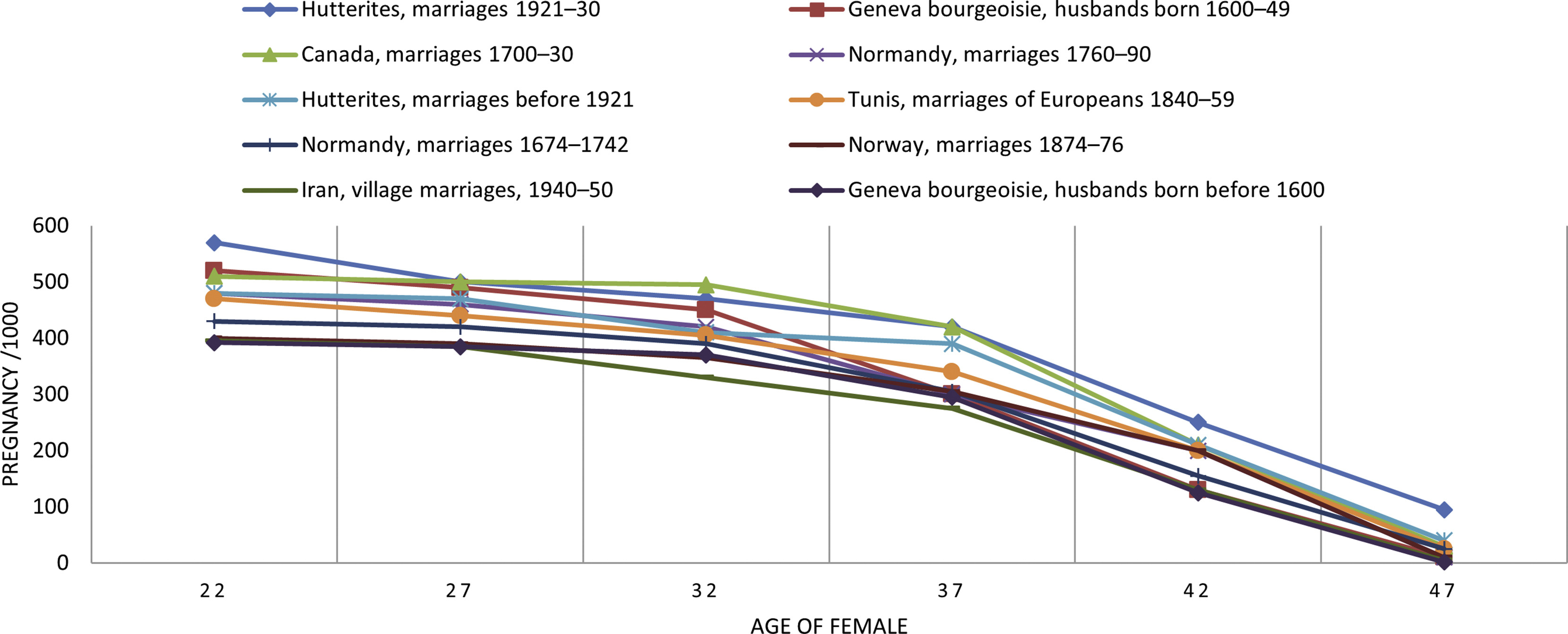
“受孕期”与排卵日的关系，排卵前 2 天内发生时受孕能力达到峰值 80%多
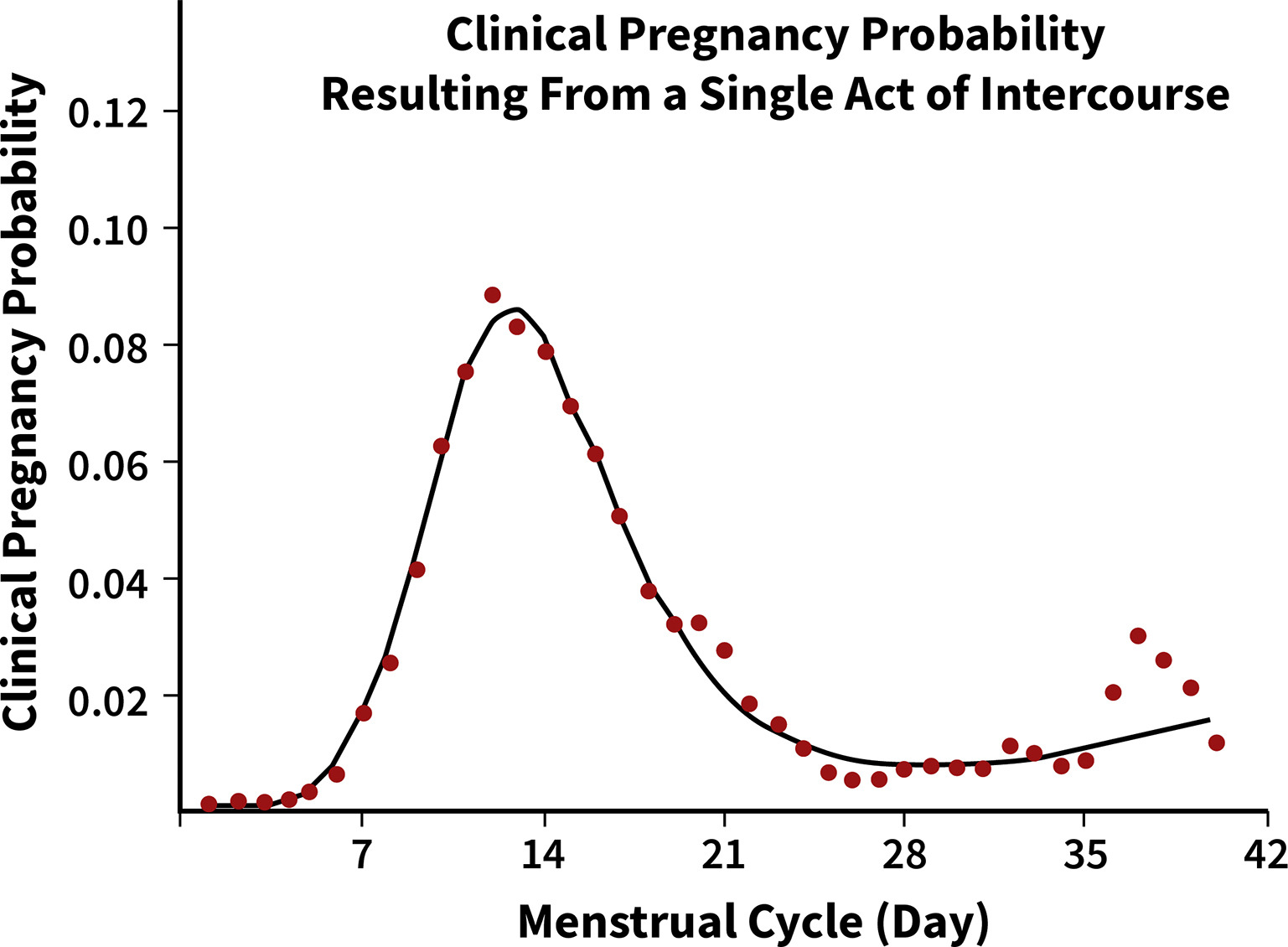
受孕一次就怀孕的概率，如果按均值，一次就怀孕的概率10%附近，次数越多越能接近峰值区域，所以四郎 20%，温太医 40%，允礼 80%
-
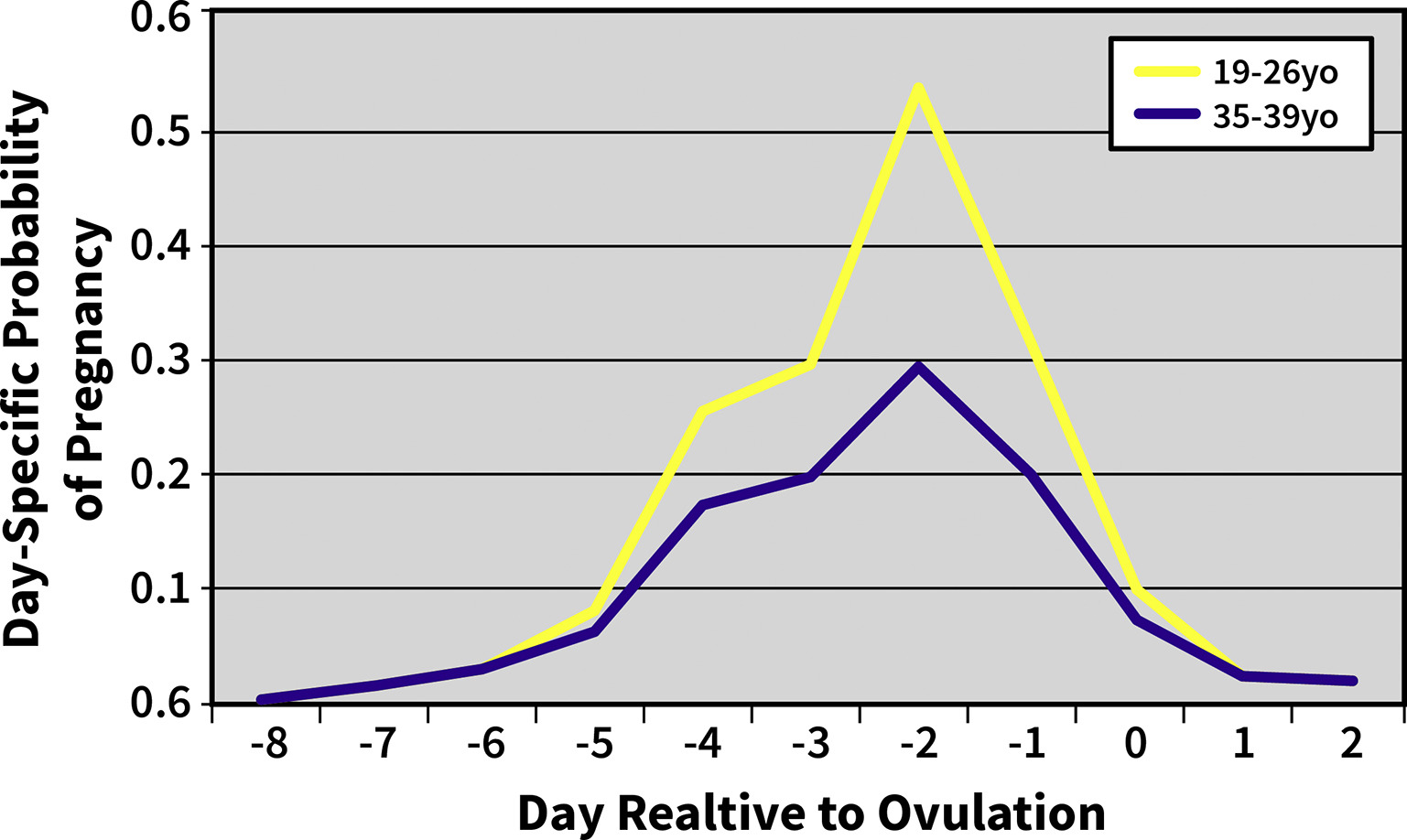
有人证的影响
皇帝能证明自己，这时候人证作用100%。有人看见温实初也有人证 30%，去过一次。允礼从宫里就跟甄嬛接触比较多，到甘露寺也见的不少 70%
似然函数考虑三方面的因素：
-
年龄影响怀孕概率：
- 四郎47岁，怀孕概率为10%（0.1）
- 允礼27岁，怀孕概率为50%（0.5）
- 温实初27岁，怀孕概率为50%（0.5）
-
见面次数影响怀孕概率：
- 四郎见甄嬛1次，怀孕概率为20%（0.2）
- 允礼见甄嬛5次，怀孕概率为80%（0.8）
- 温实初见甄嬛3次，怀孕概率为40%（0.4）
-
有人证的影响：
- 四郎能证明自己，概率为100%（1.0）
- 允礼有人证，概率为70%（0.7）
- 温实初有人证，概率为30%（0.3）
结合各因素的怀孕概率如下：
-
四郎的怀孕概率 ( P(B|A1) )：
0.1×0.2×1.0=0.02 -
允礼的怀孕概率 ( P(B|A2) )：
0.5×0.8×0.7=0.28 -
温实初的怀孕概率 ( P(B|A3) )：
0.5×0.4×0.3=0.06 -
全概率 ( P(B) )
全概率是怀孕的总概率，包括所有可能的父亲的情况。根据全概率公式：
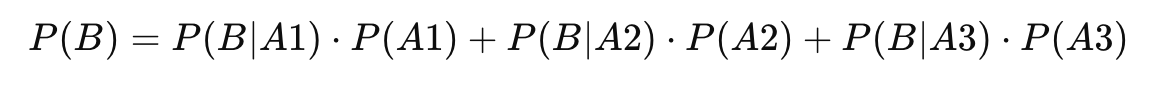
将各值代入：
P(B)=0.02⋅0.5+0.28⋅0.3+0.06⋅0.2=0.01+0.084+0.012=0.106
-
后验概率 ( P(A1|B) ), ( P(A2|B) ), ( P(A3|B) )
现在我们可以通过贝叶斯公式计算后验概率：
-
四郎是孩子父亲的概率：
-
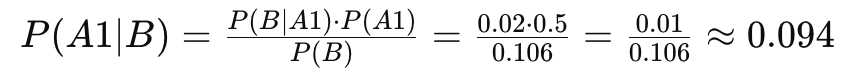
允礼是孩子父亲的概率
-
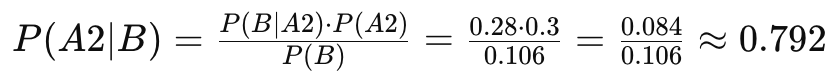
温实初是孩子父亲的概率：
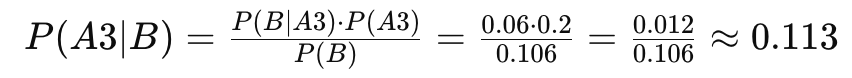
五、结果分析
通过贝叶斯算法计算，在考虑到所有影响怀孕的因素后，孩子是四郎亲生的概率约为9.4%，允礼是孩子父亲的概率约为79.2%，温实初是孩子父亲的概率约为11.3%。这个结果表明，允礼是孩子父亲的概率最高，四郎的概率最低，四郎有很高的理由怀疑孩子并非自己亲生。
六、结论
贝叶斯算法为我们提供了一种理性、系统的方法来分析复杂问题。在《甄嬛传》中，四郎通过分析甄嬛的行为和信息，可以合理地得出孩子不是自己亲生的怀疑。这不仅展现了统计学的强大工具，也为宫廷剧增添了一层理性推理的色彩。
这篇关于甄嬛传熹贵妃上户口：如果让他陪你过冬天，那朕能不能睡中间？贝叶斯模型推导爸爸去哪儿的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
