【LVGL】Guider 界面分析

本文主要是介绍【LVGL】Guider 界面分析，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前言

分析Gui Guider-1.7.2-GA 生成的 LVGL 界面切换，资源管理等处理

架构

所有控件存放于同一个结构体 lv_ui 内，每个页面都至少包含 screen_xxx 和 screen_xxx_del 两个成员

typedef struct
{lv_obj_t *screen_top;bool screen_top_del;lv_obj_t *screen_top_img_31;lv_obj_t *screen_ext;bool screen_ext_del;lv_obj_t *screen_ext_img_1;lv_obj_t *screen_ext_img_2;
}lv_ui;

控件变量定义

lv_ui guider_ui;

主程序初始化

    /*Initialize LittlevGL*/lv_init();/*Create a GUI-Guider app */setup_ui(&guider_ui);events_init(&guider_ui);custom_init(&guider_ui);

创建 UI

void setup_ui(lv_ui *ui)
{init_scr_del_flag(ui);setup_scr_screen_ext(ui);lv_scr_load(ui->screen_ext);
}

• 初始化页面标志
• 初始化第一个界面
• 加载第一个界面

切换界面

加载新屏幕前释放屏幕内存：勾选会卡顿

// screen_top 切换到 screen_std
ui_load_scr_animation(  &guider_ui,&guider_ui.screen_std,guider_ui.screen_std_del,&guider_ui.screen_top_del,setup_scr_screen_std,LV_SCR_LOAD_ANIM_NONE,200,200,false,true);

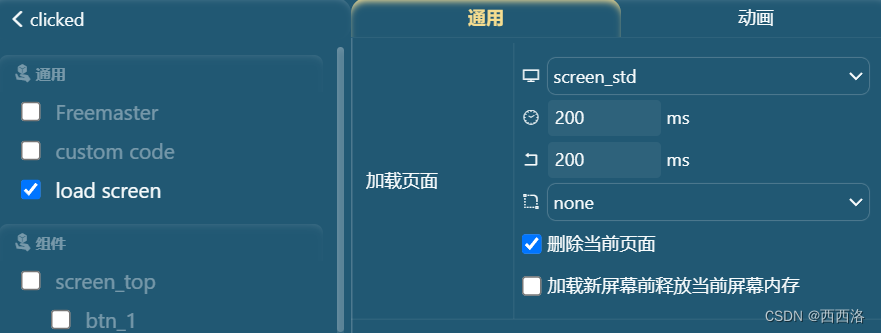
void ui_load_scr_animation(lv_ui *ui, lv_obj_t ** new_scr, bool new_scr_del, bool * old_scr_del, ui_setup_scr_t setup_scr,lv_scr_load_anim_t anim_type, uint32_t time, uint32_t delay, bool is_clean, bool auto_del)

空间释放分析

底层调用 lv_obj_del(obj) 删除控件，发现控件消失 heap_sys 空间得到了释放，heap_cma 无动于衷

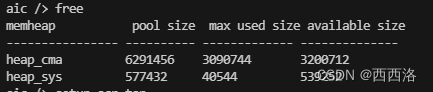
原始堆栈

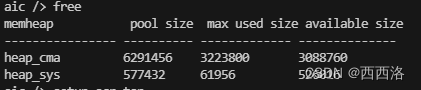
创建页面后

重入

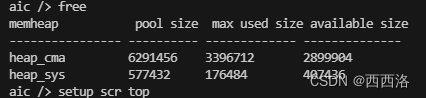
再重入

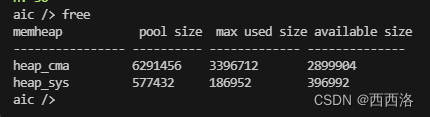
cma 空间存放图片缓存，仅第一次创建界面时变化

sys 空间存放指针信息，每次创建都会生成新的指针，每次都会减少

删除界面

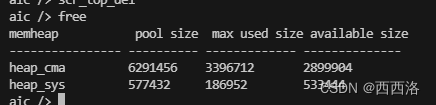
更新缓存

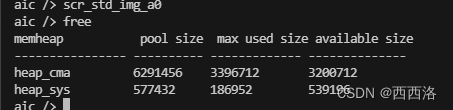
发现 cma 空间恢复如初，sys 空间有所损失

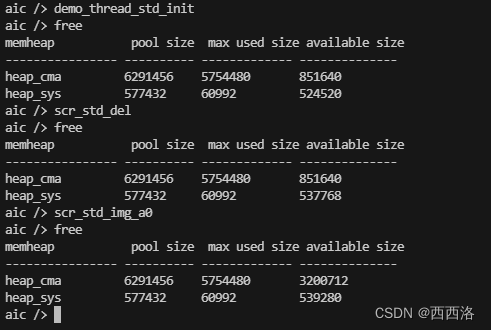
创建页面

创建空白界面

	ui->screen_std = lv_obj_create(NULL);lv_obj_set_size(ui->screen_std, 800, 480);lv_obj_set_scrollbar_mode(ui->screen_std, LV_SCROLLBAR_MODE_OFF);

更新布局

	//Update current screen layout.lv_obj_update_layout(ui->screen_std);

至此屏幕并没有实际刷新画面

加载显示画面

lv_scr_load(ui->screen_top);

空间变化

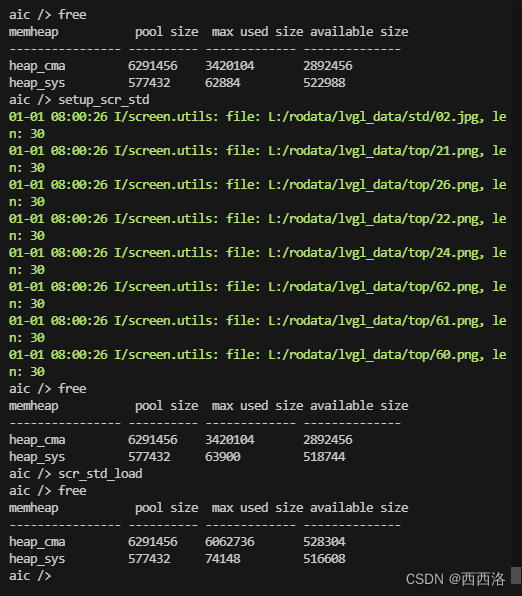
这篇关于【LVGL】Guider 界面分析的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---