本文主要是介绍终于把AUC的计算方式搞懂了!,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1. 横纵坐标
纵坐标:sensitivity或者TPR
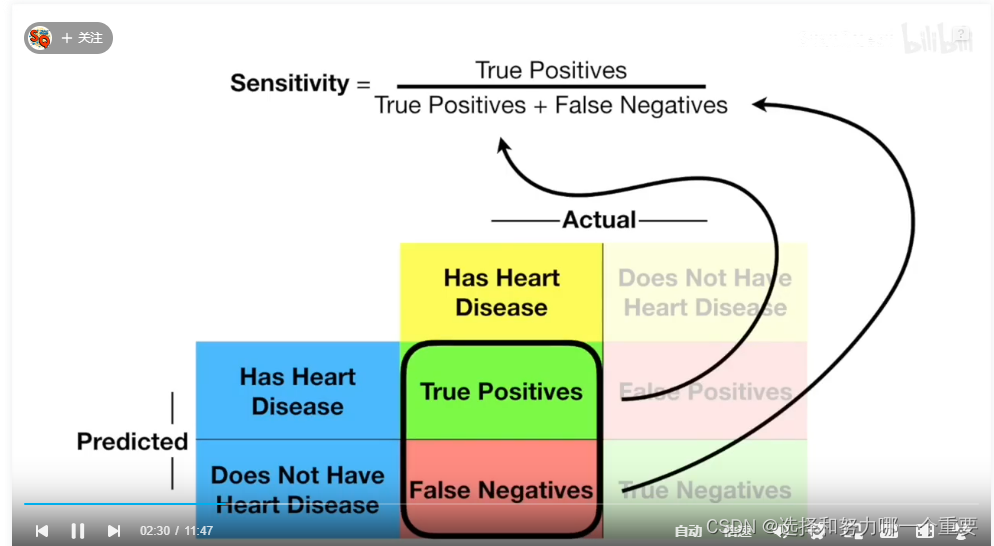
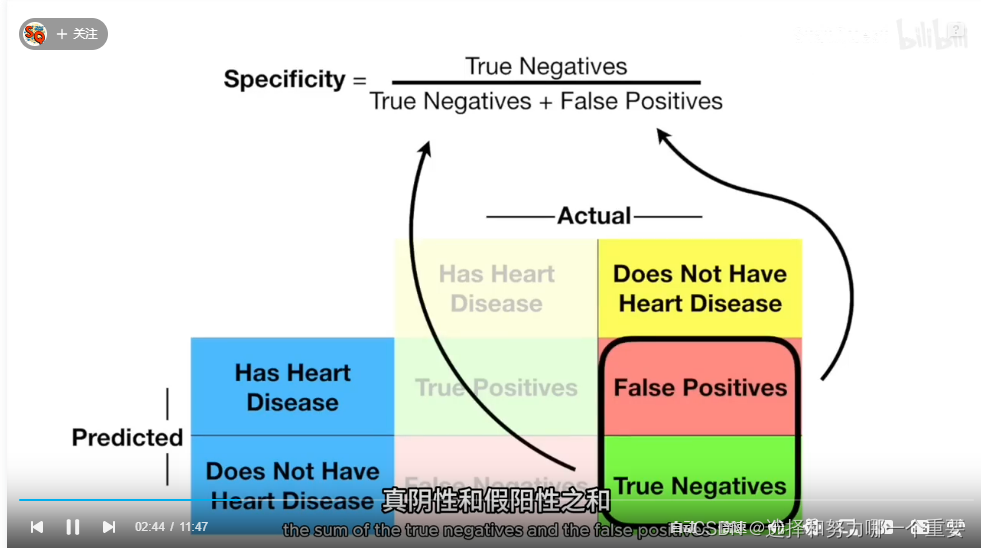
横坐标:FPR 或者 1-Specificity
2. 计算方法
2.1 方法1
def get_roc_auc(y_true, y_score):"""正样本得分大于负样本得分的概率,需要遍历每个正样本和每个负样本1. 选取所有正样本与负样本的两两组合2. 计算正样本预测值pos_score大于负样本预测值neg_score的概率:如果pos_score>neg_score,概率为1如果pos_score==neg_score,概率为0.5如果pos_score<neg_score,概率为0如果有M个正样本,N个负样本,则会产生M × N 个样本对,所以算法时间复杂度为O ( M × N ) 。:param y_true::param y_score::return:"""gt_pred = list(zip(y_true, y_score))probs = []pos_samples = [x for x in gt_pred if x[0] == 1]neg_samples = [x for x in gt_pred if x[0] == 0]# 计算正样本大于负样本的概率for pos in pos_samples:for neg in neg_samples:if pos[1] > neg[1]:probs.append(1)elif pos[1] == neg[1]:probs.append(0.5)else:probs.append(0)return np.mean(probs)
y_true = [0, 0, 1, 1, 0, 1, 0, 1, 1, 1]
y_score = [0.1, 0.4, 0.6, 0.6, 0.7, 0.7, 0.8, 0.8, 0.9, 0.9]print(get_roc_auc(y_true, y_score))2.2 方法2
根据公式计算

def get_roc_auc(y_true, y_score):ranks = enumerate(sorted(zip(y_true, y_score), key=lambda x: x[-1]), start=1)pos_ranks = [x[0] for x in ranks if x[1][0] == 1]M = sum(y_true)N = len(y_true) - Mauc = (sum(pos_ranks) - M * (M + 1) / 2) / (M * N)return auc
2.3 方法3
from sklearn.metrics import roc_auc_score
import numpy as np
y_true = np.array([1]*1693+[0]*8307)
y_score = np.random.rand(10000)
auc = roc_auc_score(y_true, y_score)
auc
这篇关于终于把AUC的计算方式搞懂了!的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








