复分析——第2章——Cauchy定理及其应用(E.M. Stein R. Shakarchi)

本文主要是介绍复分析——第2章——Cauchy定理及其应用(E.M. Stein R. Shakarchi)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

第2章 Cauchy定理及其应用

The solution of a large number of problems can be

reduced, in the last analysis, to the evaluation of definite

integrals; thus mathematicians have been much

occupied with this task... However, among many results

obtained, a number were initially discovered by

the aid of a type of induction based on the passage

from real to imaginary. Often passage of this kind

led directly to remarkable results. Nevertheless this

part of the theory, as has been observed by Laplace,

is subject to various difficulties...

After having reflected on this subject and brought

together various results mentioned above, I hope to

establish the passage from the real to the imaginary

based on a direct and rigorous analysis; my researches

have thus led me to the method which is the object of

this memoir...

( 归根结底，大量问题的求解可以归结为定积分的求值；因此，数学家们一直忙于这项任务……然而，在获得的许多结果中，有一些结果最初是借助基于从实数到虚数的过渡的归纳法发现的。通常这种类型的通过会直接带来显着的结果。然而，正如拉普拉斯所观察到的，理论的这一部分遇到了各种困难......,

在对这个主题进行反思并汇总上述各种结果后，我希望在直接而严格的分析基础上建立从实数到虚数的通道；因此，我的研究引导我找到了这本回忆录的主题的方法...... )

------------------------------------------------------------- A. L. Cauchy, 1827

在前面章节中，我们讨论了进行复分析的几个预备思想：ℂ 中的开集，全纯函数，以及循曲线积分。这个理论的第一个重要结论展示了这些概念之间的一个深层联系。大致讲来，Cauchy定理指出，若 f 在开集Ω 上是全纯函数并且γ⊂Ω 是一条其内部也包含于Ω的曲线，则

(1) $\displaystyle \int_{\gamma}f(z)dz=0$ 。

很多随合的结论(特别是留数积分(calculus of residues)都或多或少与这个事实相关。

Cauchy定理的精确和一般表述要求明确定义曲线的“内部”，而这并不总是一项容易的任务。在我们研究的早期阶段，我们将利用将自己限制在边界为“可构周线”的曲线的区域的装置。顾名思义，这些是闭合曲线，其可视化非常简单，其内部概念将是明确的，并且在这种情况下Cauchy定理的证明将非常直接。对于许多应用来说，将我们限制在这些类型的曲线上即可。在稍后的阶段，我们将讨论与更一般的曲线、它们的内部结构以及Cauchy定理的扩展形式相关的问题。

我们从Cauchy定理的初始版本首先观察到，根据第一章中的推论3.3，f 有一个 Ω 基元即可。可构周线的这种基元的存在将由 Goursat[gu:rsá]定理得出(它本身就是一个简单的定理)特殊情况)(注：Goursat 的结论是在Cauchy定理之后得出的，它的兴趣在于技术事实，即它的证明只需要每个点存在复导数，而不需要其连续性。对于早期的证明，请参见练习 5。) ,它断言，如果 f 在包含三角形 T 及其内部的开集中是全纯的，则

$\displaystyle \int_{T}f(z)dz=0$ 。

值得注意的是，Cauchy定理的这个简单例子即可证明它的一些更复杂的版本。从那里，我们可以证明一些简单区域内部原函数的存在，从而证明在这种情况下的Cauchy定理。作为该观点的首次应用，我们通过使用适当的可构周线来评估几个实积分。

上述思想也引导我们得出本章的一个中心结论，即Cauchy积分公式；这表明如果 f 在包含圆 C 及其内部的开集中是全纯的，则对于 C 内的所有 z，

$\displaystyle f(z)=\frac{1}{2\pi i}\int_{C}\frac{f(\zeta)}{\zeta - z}d\zeta$ 。

对这个恒等式微分就产生了其他积分公式，特别是我们获得了全纯函数的正则性(regularity)。这是值得注意的，因为全纯性仅假设一阶导数的存在，但我们因此获得了所有阶导数的存在。( 对于实数变量，类似的表述绝对是错误的！)

迄今为止发展的理论已经产生了许多值得注意的结果：

$\bullet$ “解析延拓(analytic continuation)”基础的性质，即全纯函数是由其定义域的任何开子集的限制来确定的。这是全纯函数具有幂级数展开这一事实的结果。

$\bullet$ Liouville定理，它可以快速证明代数基本定理。

$\bullet$ Morera定理，给出了全纯函数的简单积分表征，并表明这些函数在一到处极限下得到保留。

1. Goursat[gu:rsá] 定理(Goursat’s theorem)

前面章节的推论3.3指出,若函数 f 在一个开集Ω 上有一个原函数，则对于Ω上任意闭合曲线 γ ，都有

$\displaystyle \int_{\gamma}f(z)dz=0$ 。

反之，若我们可以证明对于若些类型的曲线γ ，以上关系成立，则一定存在一个原函数。我们的起点是Goursat定理(译注：全名Édouard Jean-Baptiste Goursat (1858年5月21日—1936年11月25日)，法国数学家)，事实上，从此，我们可以推导出本章的大部分结论。

定理 1.1 若 Ω 是 ℂ 上的一个开集，并且T⊂Ω 是一个其内部包含于 Ω 的三角形，则只要 f 在 Ω 中是全纯的，就有

$\displaystyle \int_{T}f(z)dz=0$ 。

证明：

我们称我们的原三角形为 $T^{(0)}$ (具有固定的方向，我们选其为正方向)，并令 $d^{(0)}$ 和 $p^{(0)}$ 分别表示 $T^{(0)}$ 的直径(diameter)和周长(perimeter)。我们的构造的第一步——二分三角形的每条边并将这些中点连接起来。这产生了四个新的更小的三角形，与原三角形类似，分别表示为 $T_{1}^{(1)}$ ， $T_{2}^{(1)}$ ， $T_{3}^{(1)}$ 和 $T_{4}^{(1)}$ 。每个三角形的结构和方向如图1所示。

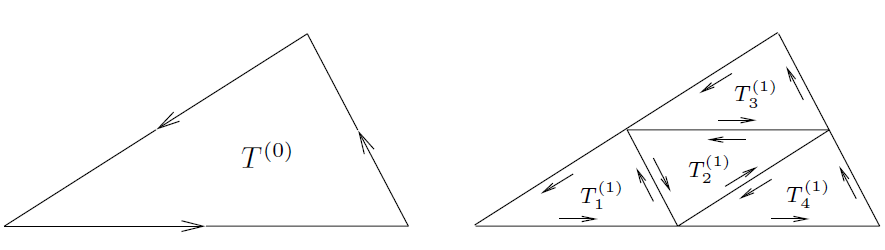
-----------------------------------------------图1： $T^{(0)}$ 二分图------------------------------------------------

所选方向与原三角形一致，在因在两个相反方向的同一侧积分而产生的抵消之后，我们得到

(2) $\displaystyle \int_{T^{(0)}} {f(z)dz} = \int_{T_{1}^{(1)}}{f(z)dz}+\int_{T_{2}^{(1)}}{f(z)dz} +\int_{T_{3}^{(1)}}{f(z)dz} +\int_{T_{4}^{(1)}}{f(z)dz}$ 。

对于某个 j ，我们一定有

$\displaystyle \left | \int_{T^{(0)}} {f(z)dz} \right | \leq 4 \left | \int_{T_{j}^{(1)}}f(z)dz \right |$ ，

否则，(2)会是矛盾的。我们选择一个满足这个不等式的三角形，并重命名为 $T^{(1)}$ 。观察到，若用 $d^{(1)}$ 和 $p^{(1)}$ 分别表示 $T^{(1)}$ ，则 $d^{(1)} = \frac{1}{2} d^{(0)}$ ， $p^{(1)} = \frac{1}{2} p^{(0)}$ 。现在我们对三角形 $T^{(1)}$ 重复这个二分过程，将其二分为四个更小的三角形。持续这个重复过程，我们就获得了一系列三角形

$T^{(0)} ,T^{(1)} ,...,T^{(n)} ,...$

且具有属性

$\displaystyle \left | \int_{T^{(0)}} {f(z)dz} \right | \leq 4^{n} \left | \int_{T^{(n)}}f(z)dz \right |$

和

$d^{(n)} = 2^{-n} d^{(0)} ,p^{(n)} = 2^{-n} p^{(0)}$ ，

其中， $d^{(n)}$ 和 $p^{(n)}$ 分别表示 $T^{(n)}$ 的直径和周长。此外，我们用 $\tau^{(n)}$ 表示具有边界 $T^{(n)}$ 的实心(solid)闭合三角形(译注：符号“𝒯”是字母T的数学体，Unicode编码“U+1D4AF”，LaTex语法“\mathcal{T}”)，并观察到，我们构造产生了一系列的内嵌紧集合(译注：参见第一章，紧集合指“闭合且有界的集合”)

$\tau^{(0)} \supset \tau^{(1)} \supset ...\supset \tau^{(n)} \supset ...$ ，

其直径趋近于 0 。根据第1 章中的命题 1.4 ,存中一个属于所有实心三角形 $\tau^{(n)}$ 的唯一点 $z_{0}$ ，因为f在点是全纯的，我们可以写成

$f (z) = f (z_{0}) + f ^{'}(z_{0})( z - z_{0} ) + \psi(z)( z - z_{0} )$ ，

(译注：符号“𝜓” 是希腊字母“Ψ”的数学体的小写，Unicode编码“U+1D713”，LaTex语法“\psi”。)

其中，随着 $z \rightarrow z_{0}$ 而 $\psi(z) \rightarrow 0$ 。由于常量函数 $f (z_{0})$ 和线性函数 $f^{'}(z_{0})( z - z_{0} )$ 具有原函数，因此，我们可以使用前面章节中的推论3.3对以上等式进行积分，并得到

(3) $\displaystyle \int_{T(n)}^{} f(z)dz = \int_{T^{(n)}}^{}\psi(z)( z - z_{0} ) dz$ 。

现在， $z_{0}$ 属于实心三角形 $\tau^{(n)}$ 闭包且 z 属于其边界，因此，我们一定有 $|z - z_0 | \leq d^{(n)}$ ,使用(3)(通过使用前面章节命题3.1的(iii)),得到估算

$\displaystyle \left | \int_{T(n)}^{} f(z)dz \right | \leq \epsilon_{n}d^{(n)}p^{(n)}$ ,

其中，随着 $n \rightarrow \infty$ 而 $\epsilon_{n} = \sup_{z \in T^{(n)}} | \psi(z) | \rightarrow 0$ 。因此，

$\displaystyle \left | \int_{T(n)}^{} f(z)dz \right | \leq \epsilon_{n}4^{n}d^{(0)}p^{(0)}$ ，

其产生了我们最后的估算

$\displaystyle \left | \int_{T(0)}^{} f(z)dz \right | \leq 4^{n}\left | \int_{T(n)}^{} f(z)dz \right | \leq \epsilon_{n} d^{(0)}p^{(0)}$ ，

令 $n \rightarrow \infty$ ，由于 $\epsilon_{n} \rightarrow 0$ ，故而推断出这个证明。

推论 1.2 若 f 在包含一个矩形 R 及其内部的开集 Ω 上是全纯的，则

$\displaystyle \int_{R}f(z)dz = 0$ 。

这是显然的，因为我们首先选择一个如图2中所示的方向，并注意到

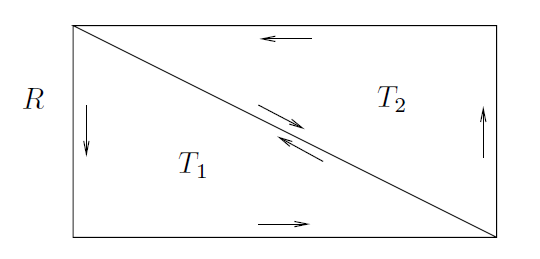
$\displaystyle \int_{R}f(z)dz = \int_{T_{1}}f(z)dz+ \int_{T_{2}}f(z)dz$ 。

---------------------------------------图2：两个(全等)三角形合成的矩形---------------------------------------

2. 圆盘中原函数的局部存在性和Cauchy定理(Local existence of primitives and Cauchy’s theorem in a disc)

我们首先根据Goursat定理证明圆盘中原函数的存在。

定理 2.1 一个开圆盘中的全纯函数有一个此圆盘中的原函数。

证明：

经过平移之后，我们可以不失一般性地假设，圆盘(比如D)以原点为圆心。已知一个点 z ∈ D ,考虑连接 0 到 z 的逐段平滑曲线，它的形成过程是某一点首先从原点沿水平方向移动到 $\tilde{z}$ (其中 $\tilde{z} = \mathrm{Re}\{z\}$ ),然后再从 $\tilde{z}$ 沿垂直方向移动到z 。我们选择从0到z的方向为正向，并用 $\gamma_{z}$ (polygonal line)，如下图3所示。

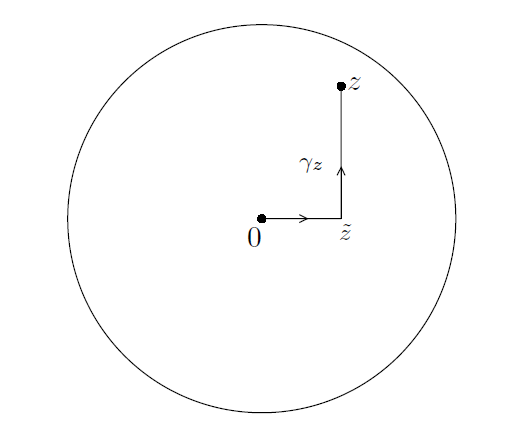
--------------------------------------------------图3：折线 $\gamma_{z}$ -----------------------------------------------

定义

$\displaystyle F(z) = \int_{\gamma_{z}}f(w)dw$ 。

$\gamma_{z}$ 的选择给出了函数 F(z) 的一种明确定义。我们声称(contend)，F 在 D 中是全纯的，并且 $F^{'}(z) = f ( z )$ 。为了证明这一点，固定 z ∈ D 且令 h ∈ ℂ 小到以使得 z + h也属于圆盘。现在考虑差值

$\displaystyle F(z + h) - F(z) = \int_{\gamma_{z+h}}f(w)dw - \int_{\gamma_{z}}f(w)dw$ 。

函数 f 首先以原点作为起点沿 $\gamma_{z+h}$ 积分，然后以与此相反的方向(原因在于第二个积分之前的减号)沿 $\gamma_{z}$ 积分。这一步对应图4中的(a)。由于我们从原点出发在两个相反的方向上在(折)线段之上对 f 进行积分，它们相互抵消了一部分，留给我们如图(b)的周线。然后，我们(按类似的构造)围成了长方体和三角形，如图(c)所示，因此，我们在对矩形和三形应用Goursat定理之后，我们得到了从z到z + h的线段，如图(d)所示。

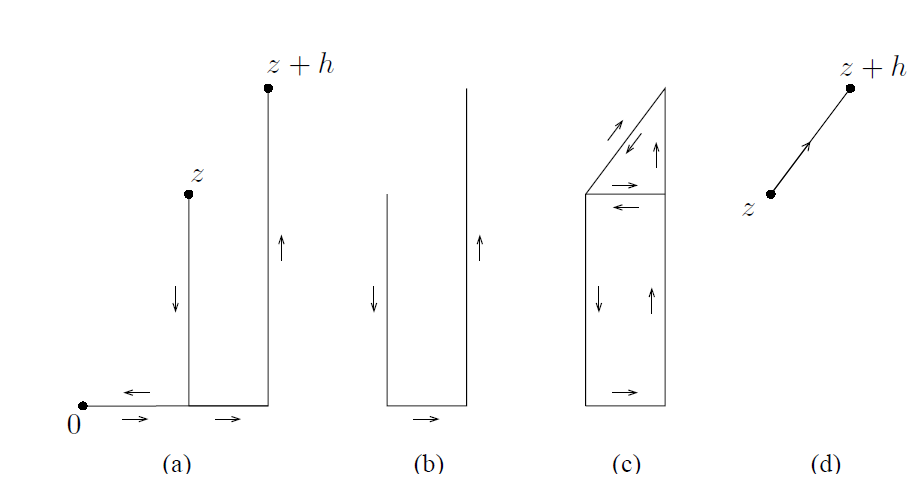
------------------------------------------图4：折线 $\gamma_{z}$ 与 $\gamma_{z+h}$ 之间的关系-------------------------------------

因此，在经上述抵消之后就产生了等式

$\displaystyle F(z + h) - F(z) = \int_{\eta}f(w)dw$ ，

其中，η 是从 z 到 z + h 的直线段。因为 f 在 z 点是连续的，因此，我们可记为

$f (w) = f (z) + \psi (w)$ ，

其中，随着 $w \rightarrow z$ 而 $\psi(w) \rightarrow 0$ 。因此，

(4) $\displaystyle F(z + h) - F(z) = \int_{\eta}f(z)dw + \int_{\eta}\psi(w)dw=f(z)\int_{\eta}dw+\int_{\eta}\psi(w)dw$ 。

在另一方面，常量1 以 w 为原函数，因此，通过简单地应用第一章中的定理 3.2，第一个积分就是 h。在另一方面，我们有下面的估算：

$\displaystyle \bigg | \int_{\eta}\psi(w)dw \bigg | \leq \sup_{w \in \eta} \left | \psi(w) \right | \left | h \right |$ 。

因为以上上确界随着h趋近于0而趋近于0 ,我们从等式(4)推导出

$\displaystyle \lim_{h \rightarrow 0}\frac{F(z+h)-F(z)}{h}=f(z)$ ，

从而，证明了 F 是 f 在圆盘上的原函数。

该定理表明，在局部，每个全纯函数都有一个原函数。然而，重要的是要认识到该定理不仅适用于任意圆盘，而且也适用于其他集合。我们将在讨论“可构周线或可构围道(toy contour)”时很快回到这一点(译注：单词“toy”有两个含义在这里可供考虑，一个是指 “玩具”或者“可把玩的东西，可拼揍、可拼接的东西”，另一个是指“微缩的东西，比标准的东西小的东西”，在这里应当是指“内部”容易识别并且在其内部可进行某种构建某种结构(即“把玩、操控、拼揍、拼接”)的围线，在此暂且将其译为“可构周线”,在汉语中,“周”和“围 ”在“闭合”的意义上是同义词,下文中的“contour”都译为“周线”)。

定理 2.2 (圆盘的Cauchy定理) 若 f 在圆盘中是全纯的，则对于此圆盘中的任意闭合曲线 γ,有

$\displaystyle \int_{\gamma}f(z)dz = 0$ 。

证明：

因为 f 有原函数，我们可以应用第一章中的推论3.3证明之。

推论 2.3 假设 f 在一个圆C及其内部的开集中是全纯的。则

$\displaystyle \int_{C}f(z)dz = 0$ 。

证明：

令 D 为具有边界圆C的圆盘，则存在一个包含D的稍微更大一点的圆盘 D’ ，使得 f在D’ 上是全纯的。现在，我们可以在 D’ 中应用Cauchy定理，从而推导出 $\int_{C}f(z)dz = 0$ 。

事实上，只要我们能够明确地定义周线的“内部”，并在该周线及其内部的开邻域中构造适当的多边形路径，该定理及其推论的证明就适用。对于内部是圆盘的圆来说，没有问题，因为圆盘的几何形状使得在其内部水平和垂直移动变得简单。

以下定义是松散的表述，尽管其应用是清晰且明确的。我们将可构周线(toy contour)定义为其内部概念明显、并且在曲线及其内部的邻域中可以进行类似于定理 2.1 中使用的那种构造的任何闭合曲线。它的正方向是当我们沿着可构周线行进时内部位于其左侧的方向。这与圆的正方向的定义是一致的。例如，圆形、三角形和矩形都是可构周线，因为在每种情况下我们都可以修改(并实际复制)前面给出的参数。

可构周线的另一个重要的例子“锁眼(keyhole)” Γ(图5所示)，我们将在Cauchy积分公式的证明中使用这个例子。它由两个几乎完整的一大一小的圆构成，通过一个窄带(narrow corridor)连接起来。Γ 的内部(我们用 $\Gamma_{int}$ 表示)是由周线围合而成的具有清晰界线的区域，并且通过足够的工作，可以赋予其准确的含义。我们在其内部固定一点 $z_{0}$ 。若 f 在Γ的一个领域及其内部是全纯的，则其中一个稍略大一点的锁眼(比如说 Λ，其内部 $\Lambda_{int}$ 包含 $\Gamma \cup \Gamma_{int}$ ) 的内部也是全纯的。若 $z \in \Lambda_{int}$ ,令 $\gamma_{z}$ 表示含于 $\Lambda_{int}$ 内且连接 $z_{0}$ 到 z 的任意曲线，这条曲线由有线多的水平或垂直线段构成(如图6所示)。若 $\eta_{z}$ 是另一条这样的曲线，Goursat定理的矩形版本(推论1.2)意味着

$\displaystyle \int_{\gamma_z} f(z)dz = \int_{\eta_z} f(z)dz$ ，

因此，我们可以在 $\Lambda_{int}$ 中明确地定义 F 。

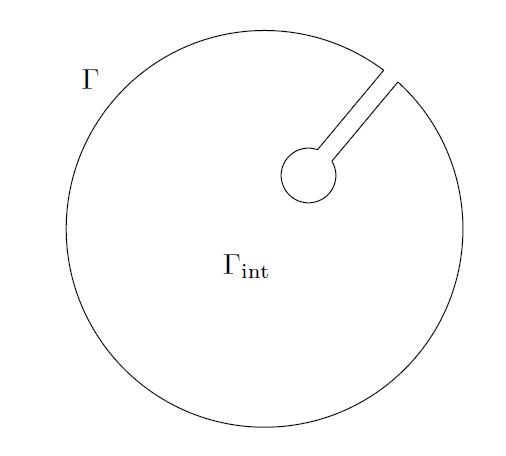
--------------------------------------------------图5：锁眼周线-----------------------------------------------------

-------------------------------------------------图 6：曲线 $\gamma_{z}$ ------------------------------------------------------

如上论证允许我们证明 F 是 f 在 $\Lambda_{int}$ 中的一个原函数，因此， $\int_{\Gamma}f(z)dz=0$ 。

中的一个原函数，因此，

$\displaystyle \int_{\gamma}f(z)dz=0$ 。

图7 给出了我们在应用中会遇到的、Cauchy定理及其推论也成立的可构周线的其他示例。

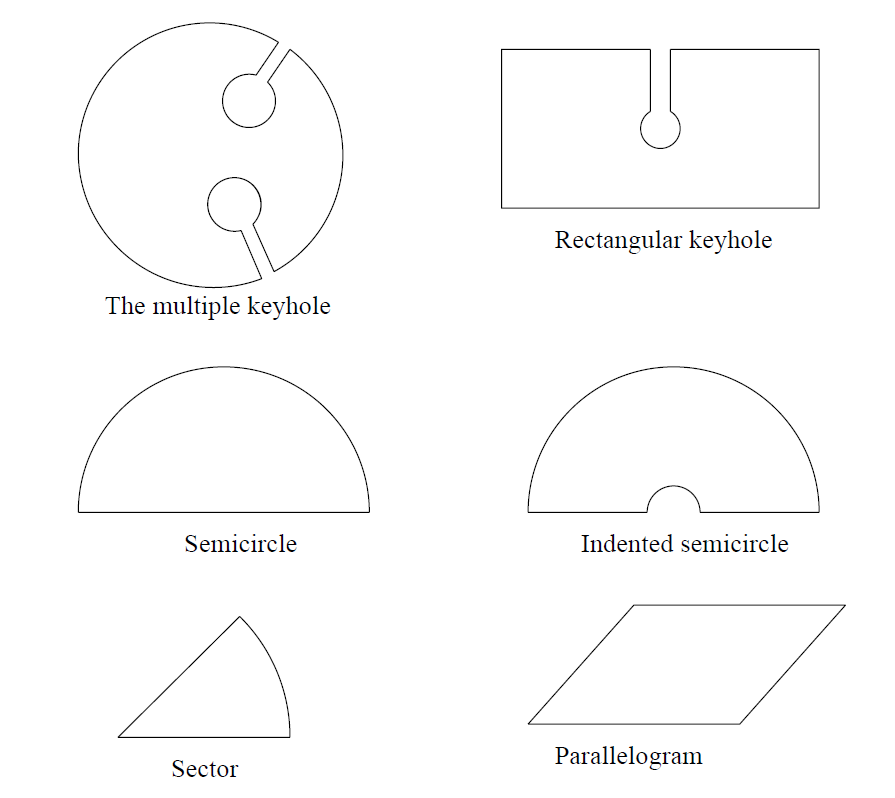
(译注：以上图形中的名称分别为

The multiple keyhole——多锁眼周线，

Semicircle——半圆周线，

Sector——半圆周线，

Rectangular keyhole——矩形锁眼周线，

Indented semicircle——凹进半圆周线，

Parallelogram——平行四边形周线。

它们的特点，都是内部非常明确清晰，因此简单。

)

------------------------------------------------图 7：可构周线的例子----------------------------------------------

虽然Cauchy可构周线定理足以满足我们处理的大多数应用，但问题仍然是对于更一般的曲线会发生什么。我们在附录 B 中讨论这个问题，并证明逐段平滑曲线的 Jordan 定理。该定理指出，简单的闭合逐段平滑曲线具有明确定义的“单连通”内部。因此，我们发现即使在这种更一般的情况下，Cauchy定理也成立。

3. 一些积分的计算(Evaluation of some integrals)

在这里，我们讨论最初激发Cauchy的思想。我们将通过几个例子来说明如何使用他的定理来计算一些积分。就留数积分而言，可以在下一章中找到更系统的方法。

例子1：

我们证明，若ξ∈ℝ ，则

(5) $\displaystyle e^{-\pi \xi^{2}}=\int_{-\infty}^{\infty}e^{-\pi x^{2}}e^{-2\pi ix\xi}dx$ 。

这给出了 $e^{-\pi x^{2}}$ 是其自身的Fourier变换这个事实(我们在第1册第5章节中的定理1.4中对其加以了证明)的一种新的证明方法。

若 ξ = 0 ,这个公式恰好是著名的积分(注：另一种推导是基于事实 $\Gamma(\frac{1}{2}) = \sqrt{\pi}$ ，其中，Γ 是第6章中讲到的gamma 函数)

$\displaystyle 1 = \int_{-\infty}^{\infty}e^{-\pi x^{2}}dx$ 。

现在，假设 ξ > 0 ,考虑函数 $f(x)=e^{-\pi x^{2}}$ (复可积函数(entire))(译注：复可积函数，又称可积函数(integral)，在整个复平面上处处解析的函数)，特别地，在图8所描绘的可构周线的内部是全纯的。

-----------------------------------------图8: 例子1中的周线 $\gamma_{R}$ -----------------------------------------------

周线 $\gamma_{R}$ 由顶点分别为 R ，R + iξ ，-R + iξ ，- R的矩形构成，并以逆时针方向为正方向。根据 Cauchy定理，

(6) $\displaystyle \int_{\gamma_{R}}f(z)dz=0$ 。

实线段部分的积分简单地为

$\displaystyle \int_{-R}^{R}e^{-\pi x^{2}}dx$ ,

当 $R \rightarrow \infty$ 时，其收敛于 1 。在右侧垂直边上的积分为

$\displaystyle I(R)=\int_{0}^{\xi}f(R+iy)idy = \int_{0}^{\xi}e^{-\pi(R^{2}+2iRy-y^{2})}idy$ 。

当 $R \rightarrow \infty$ 时，积分收敛于 0 ，因为 ξ 是固定的，我们可以通过

$\left |(R) \right | \leq Ce^{-\pi R^{2} }$

对其进行估算。类似地，基于同样的原因，在左侧垂直边上的积分随 $R \rightarrow \infty$ 而积分收敛于 0 。最后，顶部水平线段的积分是

$\displaystyle \int_{-R}^{R}e^{-\pi (x+i\xi)^{2}}dx=-e^{-\pi \xi^{2}}\int_{-R}^{R}e^{-\pi x^{2}}e^{-2\pi ix \xi}dx$ 。

因此，当 $R \rightarrow \infty$ 时，在极限中我们发现(6)给出

$\displaystyle 0=1-e^{-\pi \xi^{2}}\int_{-\infty}^{\infty}e^{-\pi x^{2}}e^{-2\pi ix \xi}dx$ ，

并建立了我们所预期的公式。在ξ < 0 的情况中，我们则考虑对称矩阵，位于下半平面。

上一个示例中使用的平移积分周线的技术还有许多其他应用。请注意，原积分(5)是在实数轴上获取的，然后再通过应用Cauchy定理在复平面中向上或向下平移(取决于 ξ 的符号)(以获得其它积分)。

例子2：

另一个经典的例子是

$\displaystyle \int_{0}^{\infty}\frac{1-\cos(x)}{x^{2}}dx=\frac{\pi}{2}$ 。

在此，我们考虑函数 $f(z) = (1 - e^{iz})/ z^2$ ，我们在位于x 轴上半平面上的凹进半圆上进行积分，如图9所示。

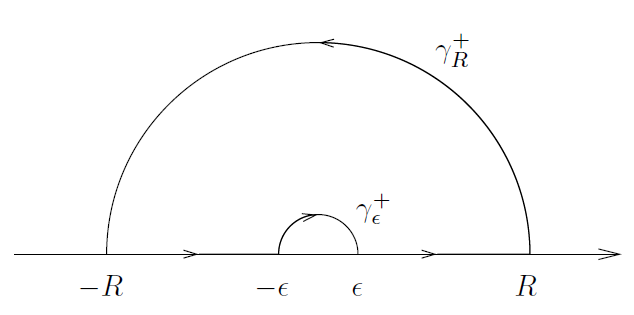
----------------------------------------------图9：例子2中的凹进半圆--------------------------------------------

若我们分别用 $\gamma_{\epsilon}^{+}$ 和 $\gamma_{R}^{+}$ 来表示半径为 ε 和 R 且具有正负方向的半圆，由Cauchy定理给出

$\displaystyle \int_{-R}^{-\epsilon}\frac{1-e^{ix}}{x^{2}}dx + \int_{\gamma_{\epsilon}^{+}}^{}\frac{1-e^{iz}}{z^{2}}dz + \int_{-\epsilon}^{R}\frac{1-e^{ix}}{x^{2}}dx + \int_{\gamma_{R}^{+}} \frac{1-e^{iz}}{z^{2}}dz = 0$ 。

首先，我们令 $R \rightarrow \infty$ 并观察到

$\displaystyle \left | \frac{1-e^{iz}}{z^{2}} \right | \leq \frac{2}{|z|^{2}}$ ，

因此， $\gamma_{R}^{+}$ 上的积分趋近于 0 。因此，

$\displaystyle \int_{|x| \geq \epsilon}\frac{1-e^{ix}}{x^{2}}dx=-\int_{\gamma_{\epsilon}^{+}}\frac{1-e^{iz}}{z^{2}}dz$ 。

然后，注意到

$\displaystyle f(z) = \frac{-iz}{z^{2}} + E(z)$ ，

其中，E(z) 当 z ⟶ 0 时是有界的。而在 $\gamma_{\epsilon}^{+}$ 上我们有 $z = \epsilon e^{i\theta}$ 且 $dz = i\epsilon e^{i\theta}d\theta$ 。因此，当 ε ⟶ 0 时 ,

$\displaystyle \int_{\gamma_{\epsilon}^{+}}\frac{1-e^{iz}}{z^{2}}dz \rightarrow \int_{\pi}^{0}(-ii)d\theta = -\pi$ 。

取实数部分，则得到

$\displaystyle \int_{-\infty}^{\infty}\frac{1-\cos(x)}{x^{2}}dx=\pi$ 。

由于被积函数是偶函数，因此，预期公式得证。

4. Cauchy积分公式(Cauchy’s integral formulas)

表达公式，特别是积分表达公式，在数学中发挥着重要作用，因为它们允许我们基于较小的集合上的行为恢复大集合上的函数。例如，我们在第一册书中看到，圆盘中的稳态热传导方程的解完全由其在圆上的边界值通过与Poisson核的卷积来确定,即

(7) $\displaystyle u(r,\theta) = \frac{1}{2\pi} \int_{0}^{2\pi}P_{r} (\theta-\varphi)u(1,\varphi)d\varphi$ 。

在全纯函数的情况下，情况是类似的，这并不奇怪，因为全纯函数的实部和虚部是调和的(harmonic)(注：这一事实是Cauchy-Riemann方程的直接结果。我们建议读者参考第一章中的练习11)。

定理 4.1 假如 f 在一个包含圆盘 D 的闭包的开集中是全纯的。若 C 表示这个具有正方向的圆盘的边界圆，则对于任意点 z ∈ D，有

$\displaystyle f(z)=\frac{1}{2\pi i}\int_{C}\frac{f(\zeta)}{\zeta-z}d\zeta$ 。

证明：

固定 z ∈ D ，并考虑忽略了点z 的“锁眼” $\gamma_{\delta,\epsilon}$ ，如下图 10 所示。

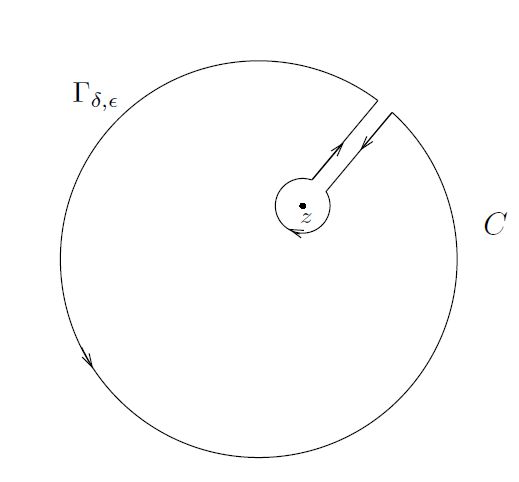
----------------------------------------------图10: 锁眼 $\gamma_{\delta,\epsilon}$ ----------------------------------------------------

其中，δ是通道(corridor)的宽度，而 ε 是以 z 为圆心的小圆的半径，因为函数 F( ζ ) = f ( ζ )/( ζ – z ) 在远离点 ζ = z 处是全纯的，则对于我们所选择的可构周线，根据Cauchy定理，我们有

$\displaystyle \int_{\gamma_{\delta,\epsilon}}F(\zeta)d\zeta = 0$ 。

现在我们通过令δ趋近于0的方式使通道变得更窄，并利用F的连续性，进而可以看到，在极限中，在通道两侧上的积分抵消掉了。余下部分包括2条曲线——具有正方向的大边界圆C，以及圆心位于 z 点半径为ε 且面向负方向(即，时钟前行方向)的小圆 $C_{\epsilon}$ 。为了理解在小圆上的积分发生了什么，我们将 F( ζ ) 改写成

(8) $\displaystyle F(\zeta)=\frac{f(\zeta)-f(z)}{\zeta - z}+\frac{f(\zeta)}{\zeta-z}$ ，

并注意到，因为 f 是全纯的，因此 (8) 式的右边第一项是有界的，故而随着 ε⟶ 0 其在小圆 $C_{\epsilon}$ 上的积分趋近于 0 。为了推导出证明，只需观察到以下事实即可：

$\begin{array}{rlc}\displaystyle \int_{C_{\epsilon}}\frac{f(z)}{\zeta-z}d\zeta &=f(z)\displaystyle \int_{C_{\epsilon}}\frac{d\zeta}{\zeta-z} \\ \\ &\displaystyle =-f(z)\int_{0}^{2{\pi}}\frac{\epsilon ie^{-it}}{\epsilon e^{-it}} \\ \\ &\displaystyle =-f(z)2{\pi}{i} \end{array}$ ，

因此，在极限中，我们求得

$\displaystyle 0=\int_{C}\frac{f(\zeta)}{\zeta-z}d\zeta-2{\pi}{i}f(z)$ ，

因此定理得证。

评注：

我们之前对可构周线的讨论提供了Cauchy积分公式的简单扩展；例如，如果 f 在包含(正向)矩形 R 及其内部的开集中是全纯的，则只要 z属于R的内部，就有

$\displaystyle f(z)=\frac{1}{2{\pi}{i}} \int_{R}\frac{f(\zeta)}{\zeta-z}d\zeta$ 。

为了建立这个结论，只需重复定理4.1的证明过程，在过程中使用矩形锁眼代替“圆形的”锁眼即可。

另外还应注意，以上积分当 z 在R之外时消没，因为，在这种情况下，F( ζ ) = f ( ζ )/( ζ – z ) 在R内是全纯的。显然，对于圆或其它可构周线，类似的结论也成立。

作为Cauchy积分公式的推论，我们得到了关于全纯函数的第二个显著事实，即它们的正则性(regularity) (译注：“则”即“规则”，正则即“非常规则”，或称规则性)。我们还获得了进一步的积分公式——根据边界上的 f 值来表示圆盘内 f 的导数。

推论 4.2 若 f 在开集 Ω上是全纯的，则 f 在 Ω上具有无限复导数。此外，若 C ⊂ Ω 是一个其内部也含于 Ω 中的圆，则对于在C内部的所有 z 有

$\displaystyle f^{(n)}(z)=\frac{n!}{2{\pi}{i}}\int_{C}\frac{f(\zeta)}{(\zeta-z)^{n+1}}d\zeta$ 。

我们记得，与前面的定理一样，我们取具有正方向的圆 C 。

证明：

通过在n上进行归纳进行证明，n = 0 这种情况不过是Cauchy积公公式。假设 f 有多达 n – 1 个复导数且

$\displaystyle f^{(n-1)}(z)=\frac{(n-1)!}{2{\pi}{i}}\int_{C}\frac{f(\zeta)}{(\zeta-z)^{n}}d\zeta$ 。

现在，对于 h 极小量， $f^{(n-1)}$ 的差商取为

(9) $\displaystyle \frac{f^{(n-1)}(z+h)-f^{(n-1)}(z)}{h}=\frac{(n-1)!}{2\pi{i}}\int_{C}f(\zeta)\frac{1}{h}\left [\frac{1}{(\zeta-z-h)^{n}-(\zeta-z)^{n}} \right ]$ 。

现在，我们记得

$A^{n} - B^{n} = (A - B)[ A^{n-1} + A^{n-2} B + ... + AB^{n-2} + B^{n-1}]$ 。

取 A = 1/(ζ – z - h)，B = 1/(ζ – z ) , 我们看到，等式(9)中括号中的项等于

$\displaystyle \frac{h}{(\zeta-z-h)(\zeta-z)}[ A^{n-1} + A^{n-2} B + ... + AB^{n-2} + B^{n-1}]$ 。

但观察到，若 h 足够小，则 z + h与 z 停留在一个距边界圆C有限的距离，因此，在极限中随着 h 趋近于 0 ，我们求得这个商式收敛于

$\displaystyle \frac{(n-1)!}{2\pi{i}}\int_{C}f(\zeta)\left [ \frac{1}{(\zeta-z)^{2}}- \frac{n}{(\zeta-z)^{n-1}} \right ]= \frac{n!}{2\pi{i}}\int_{C}\frac{f(\zeta)}{(\zeta-z)^{n+1}}d\zeta$ ，

这就完成了归纳论证并证明了推论。

从现在开始，我们称定理 4.1 和推论 4.2 的公式为Cauchy积分公式。

推论 4.3 (Cauchy不等式) 若 f 在包含以 $z_{0}$ 为圆心以R 为半径的一个圆盘的开集中是全纯的，则

$\displaystyle \left | f^{(n)}(z_{0}) \right | \leq \frac{n! \|f\|_{C}}{R^{n}}$ ，

其中， $\| f\|_{C} \leq \sup_{z \in {C}}{|f(z)|}$ 表示边界圆 C 上的 f 的上确界。

证明：

对 $f^{(n)}(z_{0})$ 应用 Cauchy 积分公式，我们获得

$\begin{array}{rlc} \displaystyle \left | f^{(n)}(z_{0}) \right |&\displaystyle=\left | \frac{n!}{2\pi{i}}\int_{C}\frac{f(\zeta)}{(\zeta-z_{0})^{n+1}}d\zeta \right | \\ \\ &\displaystyle=\frac{n!}{2\pi}\left | \int_{0}^{2\pi}\frac{f(z_{0}+Re^{i\theta})}{(Re^{i\theta})^{n+1}}Rie^{i\theta}d\theta \right | \\ \\ &\displaystyle \leq \frac{n!}{2\pi}\frac{\|f\|_C}{R^{n}}2{\pi} \end{array}$ 。

Cauchy积分公式的另一个震撼的结果是其与幂级数的关联。在第一章中，我们证明了幂级数在收敛圆盘内部是全纯的，并给出了其逆函数的证明，这就是下一个定理的内容。

定理 4.4 假设 f 在一个开集 Ω 上是全纯的。若 D 是一个以 $z_{0}$ 为圆心且其闭包含于Ω 中的圆盘，则对于任意 z ∈D ， f 在 $z_{0}$ 处都有一个幂级数展式

$\displaystyle f (z) = \sum_{n=0}^{\infty}a_{n}(z- z_{0})^{n}$ ，

且对于任意 n ≥ 0 , 其系数由

$\displaystyle a_{n} =\frac{f^{(n)}(z_{0})}{n!}$

给出。

证明：

固定 z ∈D 。根据 Cauchy积分公式，我们有

(10) $\displaystyle f(z)=\frac{1}{2{\pi}{i}} \int_{C}\frac{f(\zeta)}{\zeta-z}d\zeta$ ，

其中，C 表示圆盘边界且 z ∈D 。将这个表述公式化为

(11) $\displaystyle \frac{1}{\zeta-z}=\frac{1}{\zeta-z_{0}-(z-z_{0})}=\frac{1}{\zeta-z_{0}}\frac{1}{1-\left (\frac{z-z_{0}}{\zeta-z_{0}} \right )}$ ，

并使用等比级数展式。因为ζ∈C 和 z ∈D 是固定的，则存在 0 < r < 1 使得

$\displaystyle \left |\frac{z-z_{0}}{\zeta-z_{0}} \right |<r$ ，

因此，

(12) $\displaystyle \frac{1}{1-\left (\frac{z-z_{0}}{\zeta-z_{0}} \right )}=\sum_{n=0}^{\infty}\left (\frac{z-z_{0}}{\zeta-z_{0}} \right )^{n}$ ，

其中，对于ζ∈C ，这个级数一致收敛。当我们将 (10),(11)和(12)结合起来的时候，这就允许我们用积分更替无限和，从而获得

$\displaystyle f(z)=\sum_{n=0}^{\infty}\left (\frac{1}{2\pi{i}} \int_{C}\frac{f(\zeta)}{(\zeta-z_{0})^{n+1}}d\zeta\right )(z-z_{0})^{n}$ 。

这就证明了幂级数展式；对导数(或级数的简单微分)进一步利用Cauchy积分公式，就证明了系数 $a_{n}$ 的公式。

观察到，由于幂级数定义了无限(复)可微函数，该定理给出了全纯函数自动无限可微的另一个证明。

另一个重要的观察点是，圆心位于 $z_{0}$ 的 f 的幂级数展式在任意圆盘上收敛(不管此圆盘有多大，只要其闭包含于 Ω )。特别地，若 f 是复可积函数(entire function)(即，在整个ℂ 上是全纯的,或称在整个ℂ上是解析的)，这个定理表明，f 围绕 0 有幂级数展式，比如， $f(z)=\sum_{n=0}^{\infty}a_{n}z^{n}$ 在整个 ℂ 上收敛。

推论 4.5 (Liouville[lju:ví:l]定理) 若 f 是复可积函数且有界，则 f 是常量。

证明：

由于ℂ是连通的，则我们可以应用第一章中的推论3.4，即可证明 $f^{'}=0$ ，对于每一个 $z_{0} \in C$ 及任一个 R > 0 , Cauchy不等式产生

$f^{'}(z_{0}) \leq \frac{B}{R}$ , 其中，B 是 f 的一个界。令 $R \rightarrow \infty$ 就给出了预期的结果。

作为我们迄今为止工作的一个应用，我们可以给出代数基本定理的一个优雅证明。

推论 4.6 任意一个具有复系数的非常量多项式 $P(z) = a_{n} z^{n} + ...+ a_{0}$ 在 ℂ 中都有一个根。

证明：

若 P 没有根，则 1/P(z) 是一个有界全纯函数。为了理解这一点，我们显然可以设 $a_{n} \neq 0$ 并将多项式写成

$\displaystyle \frac{P(z)}{z^{n}} = a_{n} + \left (\frac{a_{n-1}}{z} .. +\frac{a_{0}}{z^{n}} \right )$ ，

其中，z ≠ 0 。因为括号中的每一项随着 $| z | \rightarrow \infty$ 而趋近于 0 ，则我们可以推断出存在 R > 0 使得，若 $c = a_{n}/2$ , 则只要 | z | > R ，就有

$P(z) \geq c|z|^{n}$ 。

由于 P 是连续的且在圆盘 | z |≤R 中没有根，因此它也受到该圆盘下方的限制，从而证明了我们的断言。

根据 Liouville 定理，则我们可以推断出 1/P是常量。这与我们的假设P是非常量矛盾，因此证明了推论。

推论 4.7 次数 $n \geq 1$ 的每一个多项式 $P(z) = a_{n} z^{n} + ...+ a_{0}$ 在ℂ中都恰好有n个根。若这些根分别用 $w_{1} ,..., w_{n}$ 表示，则 P 可以被因式分解为

$P(z) = a_n(z - w_{1}) (z - w_{2})...(z - w_{n})$ 。

证明：

根据前面的结论，P 有一个根，比如为 $w_{1}$ 。则写成 $z = (z - w_{1}) + w_{1}$ ,在 P 中插入z的这个表达式，并利用二项式公式(binomial formula)，则我们得到

$P(z) = b_{n} (z - w_{1})^{n} + ...+ b_{1}(z - w_{1}) + b_{0}$ 。

其中， $b_{0} ,...,b_{n-1}$ 是新的系数，且 $b_{n} = a_{n}$ 。由于 $P(w_{1}) = 0$ , 我们求得 $b_{0} = 0$ ，因此

$P(z) = b_{n} (z - w_{1})^{n} + ...+ b_{1}(z - w_{1}) = (z-w_{1})Q(z)$ ，

其中，Q 是 n – 1 次多项式。基于多项式的次数应用归纳法，我们推导出 P(z) 具 n 有个根，且对于某个 c∈ℂ 可表示为

$P(z) = c(z - w_{1})(z - w_{2})...(z - w_{n})$ 。

展开右侧，我们认识到 $z^{n}$ 的系数是 c ，因此， $c=a_{n}$ 如断言所指。

最后，我们以分析延拓(analytic continuation，或称解析延拓)的讨论来结束本节(我们在引言中提到的第三个“奇迹(miracles)”)。它指出，如果我们知道全纯函数在适当的任意小子集上的值，则该全纯函数的“遗传密码(genetic code)”就被确定了(即该函数是固定的)。请注意，在下面的定理中，假设 Ω 连通。

定理 4.8 若 f 在区域Ω中是全纯函数，并且在一系列不同的点上消没于 Ω 中的一个极限点。则 f 恒为0 。

换句话说，若连通开集Ω中的一个全纯函数 f 的零点(译注：可能有多个)都积聚于Ω中，则 f = 0 。

证明：

假设 $z_{0}\in \Omega$ 是序列 $\{w_{k}\}_{k=1}^{\infty}$ 的一个极限点并假设 $f(w_{k})=0$ 。首先，我们证明在一个包含 $z_{0}$ 的小圆盘中恒为0 。为此，我们选择一个以 $z_{0}$ 为圆心且含于Ω 的圆盘D ，则考虑位于此盘中的 f 的幂级数展式

$\displaystyle f (z) = \sum_{n=0}^{\infty}a_{n}(z- z_{0})^{n}$ 。

若 f 不恒为0 ,则存在最小整数 m ，使得 $a_{m} \neq 0$ 。但随之我们可以写成

$f (z) = a_{m}(z- z_0)^{m}(1 + g(z - z_{0}))$ ，

其中， $g(z - z_{0})$ 随着 $z \rightarrow z_{0}$ 而收敛于 0 。取 $z = w_{k} \neq 0$ 为一系列收敛于 $z_{0}$ 的点，我们得出一个矛盾，因为 $a_{m}(w_{k}- z_{0})^{m} \neq 0$ 且 $1 + g(z - z_{0}) \neq 0$ ，但 $f (w_{k}) = 0$ ，这是不可能的。

使用Ω是连通性这个事实可以推导出这个证明。令 U 表示满足 f (z) = 0 的点集的内部。则根据定义 U是开集，并且根据刚才的论证U是非空的。集合U也是闭合的，因为 $z_{n}\in U$ 且 $z_{n} \rightarrow z$ ，则根据连续性(continuity) f (z) = 0 ,并且根据以上论证，f 在z的领域消没。因此，z∈U 。此时，若我们令 V 表示 U 在 Ω 中的补集，则我们可以推断出 U 和 V 皆为开集，且不相交，进而有

Ω = U∪V 。

因为Ω 是连通的，我们推断出 U或V是空集。(在此，我们利用了第一章中讨论连通性的的2个等价定义之一。) 由于 $z_{0}\in U$ ，我们求得 U = V ，则此证明完结。

本定理的一个直接推论如下。

推论 4.9 假设 f 和 g在一个域 Ω 上全纯的，且对于Ω的某个非空开子集中的任意z (或者，更一般地，对于某些在Ω中具有极限点的不同点的序列中的z)有 f (z) = g(z)。则贯穿整个Ω，都有 f (z) = g(z) 。

假设给我们一对分别位于Ω 和 Ω’ 上的解析函数 f 和 F 且Ω ⊂ Ω’。若这两个函数在更小的集合Ω上一致，则我们称 F 是 f 的一个向域 Ω’ 的解析拓展(analytic continuation)。则这个推论确保了仅存在一个这样的解析拓展，因为F由f唯一地确定。

5. 进一步应用(Further applications)

我们在本节中收集了迄今为止已被证明的结论的各种推论。

5.1 Morera[mərírə]定理(Morera’s theorem)

在此已被证明的一个直接应用是Cauchy定理的逆定理。

定理 5.1 假设 f 是一个位于开圆盘 D 中、并使得对于含于 D 中的任意三角形T，都有

$\displaystyle \int_{T}f(z)dz = 0$

的连续函数，则函数 f 是全纯的。

证明：

按照定理 2.1的证明方法，函数 f 在D中有一个满足 F ’ = f 的原函数F。根据正则定理(regularity theorem)，我们知道 f 是无限复可微的(因此当然是二次可微的)，因此，f 是全纯的。

5.2 全纯函数序列(Sequences of holomorphic functions)

定理 5.2 若 $\{f_{n}\}_{n=1}^{\infty}$ 是一个在每一个Ω的紧子集(compact subset)中一致收敛于一个函数f 的全纯函数序列，则 f 在 Ω 中是全纯的。

证明：

令 D 为其闭包含于 Ω中的任意圆盘，并令T为这个圆盘中的任意三角形。则由于每个 $f_{n}$ 都是全纯的，则对于所有的 n ，根据Goursat定理有

$\displaystyle \int_{T}f_{n}(z)dz = 0$ 。

根据假设，在 D 的闭包中， $f_{n} \rightarrow f$ 是一致地，因此 f 是连续的，并且有

$\displaystyle \int_{T}f_{n}(z)dz \rightarrow \int_{T}f(z)dz$ 。

最后，我们求得 $\int_{T}f_{n}(z)dz=0$ ，并且根据 Morera 定理，我们推断出 f 在D中是全纯的。因为这个结论对于其闭包含于 Ω中的每一个 D 都成立，所以我们求得 f 在整个Ω中都是全纯的。

这是一个在实变量的情况下明显不成立的震撼结论：连续可微函数的一致极限未必可微。例如，我们知道，[0,1]上的每一个连续可微函数都可以用多项式一致地逼近，根据 Weierstrass定理(见第I册第5章)，然而，并非每一个连续函数都是可微的(译注：例如，带有尖角的函数)。

我们可以进一步推导出导数级数的收敛定理。我们记得，若 f 是一个收敛半径为 R 的幂级数，则可以通过对 f 这个级数逐项微分而求得 f ’ ，此外，f ’ 的收敛半径也为 R 。(见第1章定理2.6 。) 特别地，这意味着，若 $S_{n}$ 是 f 的部分和，则 $S_{n}^{'}$ 在f 的收敛圆盘的每一个紧子集上一致收敛于 f ’ 。下一个定理概括这个事实。

定理 5.3 在前述定理的假设之下，导数级数 $\{f_{n}^{'}\}_{n=1}^{\infty}$ 在Ω 的每一个紧子集合上一致收敛。

证明：

我们可以不失一般性地假设，定理中的函数级数在整个 Ω上一致收敛。给定 δ > 0 ,令 $\Omega_{\delta}$ 表示Ω的子集，定义为

$\Omega_\delta = \{ z\in \Omega : \overline{D_\delta}(z) \subset \Omega \}$ 。

换句话说， $\Omega_{\delta}$ 由Ω中距离其边界的距离 > δ 的所有点构成。为了证明这个定理，只需证明对于每一个δ， $\{f_{n}^{'}\}$ 在 $\Omega_{\delta}$ 上一致收敛于 f ’ 即可。可以通过证明下列不等式来实现：只要F 在Ω上是全纯的,则

(13) $\displaystyle \sup_{z \in \Omega_{\delta}}\left |F^{'}(z) \right | \leq \frac{1}{\delta} \sup_{\zeta \in \Omega} \left |F(\zeta) \right |$ ，

此后，则可以被应用到 $F = f_{n} - f$ 来证明期望的事实。从 Cauchy 积分公式和 $\Omega_{\delta}$ 的定义可立即推导出(13)，因为对于每一个 $z \in \Omega_{\delta}$ , $\mathrm{D}_{\delta}(z)$ 的闭包含于 Ω 且

$\displaystyle F^{'}(z)=\frac{1}{2\pi{i}}\int_{\Omega_{\delta}(z)}\frac{F(\zeta)}{(\zeta-z)^{2}}d\zeta$ 。

因此，

$\begin{array}{rlc}\displaystyle \left | F^{'}(z) \right | &\displaystyle \leq \frac{1}{2\pi}\int_{C_{\delta}(z)}\frac{|F(\zeta)|}{|\zeta-z|^{2}}|d\zeta| \\ \\ &\displaystyle \leq \frac{1}{2\pi}\sup_{\zeta \in \Omega}|F(\zeta)|\frac{1}{\delta^{2}}2{\pi}\delta \\ \\ &\displaystyle=\frac{1}{\delta}\sup_{\zeta \in \Omega}|F(\zeta)| \end{array}$ ，

正如所要证明的。

当然，第一个导数并无特别之处，事实上，在最后一个定理的假设下，我们可以推断出(如上论证)，对于每一个 k ≥ 0 , 第 k 项导数级数 $\{f_{n}^{(k)} \}_{n=1}^{\infty}$ 在Ω 的每一个紧子集上一致收敛于 $f^{(k)}$ 。

在实践中，人们通常使用定理 5.2 来将全纯函数(比如说，具有规定的属性)构造为一个级数

(14) $\displaystyle F (z) = \sum_{z=1}^{\infty}f_{n}(z)$ 。

事实上，若每一个 $f_{n}$ 在复平面的一个已知区域 Ω 中是全纯的，且级数在Ω的紧子集合中一致收敛，则定理 5.2 确保了F 在Ω 中也是全纯的。例如，按像(14)的收敛级数所描述的各种特殊函数通常都是全纯的。具体的例子是第6章中的Riemann ζ 函数。

现在我们转向这个思想的一个变体，它由按积分定义的函数组成。

5.3 按积分定义的全纯函数(Holomorphic functions in terms of integrals)

正如我们将在本书后面看到的，许多其他特殊函数是根据

$\displaystyle f(z) = \int_{a}^{b}F(z,s)ds$

这种类型的积分定义的，或者作为这种类型的积分的极限定义。因此，函数 F 按第一个参数是全纯的，百按第二个参数是连续的。在Riemann积分的意义上在有界区间[a,b]上对积分进行积分。那么问题是确定 f 是全纯的。

在下一个定理中，我们对 F 施加一个在实践中经常满足的充分条件，这很容易暗示 f 是全纯的。

在经过简单的变量线性替换之后，我们可以假设 a = 0 和 b = 1 。

定理 5.4 令 F(z,s) 为对 (z,s)∈Ω×[0,1] 定义的函数，其中，Ω 是 ℂ 中的一个开集。假设 F 满足下列属性：

(i) 对于每一个s ，F(z,s) 按 z 是全纯的。

(ii) F 在 Ω×[0,1] 上是全纯的。则，按

$\displaystyle f(z) = \int_{a}^{b}F(z,s)ds$

定义在 Ω 上的函数 f 是全纯的。

这第二个条件指的是，F 按两个参数都是联合连续的。

为了证明这个结论，只需证明f在含于Ω中的任意圆盘D中是全纯的即可，而利用Morera定理，通过证明对于含于D 中的任意三角形T，我们有

$\displaystyle \int_{T}\int_{0}^{1}F(z,s)dsdz=0$ ，

便可实现这一点。

交换积分的顺序并使用属性 (i) 将产生期望的结果。然而，我们可以通过不同的论证来规避证明积分顺序变化合理性的问题。这个思想是将积分解释为Riemann和的“一致”极限，然后再应用上一节的结果，从而达到目的。

证明：

对于每一个 n ≥ 1 ，我们考虑 Riemann 和

$\displaystyle f_{n}(z)=(1/n)\sum_{k=1}^{n}F(z,k/n)$ 。

则根据属性(i) ， $f_{n}$ 在整个Ω上是全纯的，并且我们断言，在任意其闭包含于 Ω 的圆盘 D 中，级数 $\{f_{n} \}_{k=1}^{\infty}$ 一致收敛于f 。为了理解这一点，我们可以回顾一下一个紧集合上的一个连续函数一致连续这个事实，若任给一个 ε > 0 ,存在一个δ > 0 ，使得只要 $|s_{1} - s_{2}| < \delta$ ，就有

$\displaystyle \sup_{z \in D}\left |F(z,s_{1})-F(z,s_{2}) \right | < \epsilon$ 。

则，若 n ≥ 1/δ 且 z∈D ，我们有

$\begin{array}{rlc} \bigg | f_{n}(z)-f(z) \bigg |&=\displaystyle \bigg | \sum_{k=1}^{n} \int_{(k-1)/n}^{k/n}\bigg (F(z,k/n)-F(z,s) \bigg ) ds \bigg | \\ \\ &\displaystyle \leq \sum_{k=1}^{n} \int_{(k-1)/n}^{k/n}\bigg |F(z,k/n)-F(z,s) \bigg | ds \\ \\ & \displaystyle < \sum_{k=1}^{n}\frac{\epsilon}{n} \\ \\ & \displaystyle < \epsilon \end{array}$ 。

这就证明了我们的断言，并根据定理 5.2, 我们推断出f在D中是全纯的。因此，f在Ω中是全纯的，定理得证。

5.4 Schwarz[swɔːts]反射原理(Schwarz reflection principle)

在实际分析中，存在多种情况，人们希望将函数从给定的集合扩展到更大的集合。存在多种技术可以为连续函数提供扩展，更一般地，为具有不同平滑度的函数提供扩展。当然，随着我们对扩展施加更多条件，该技术的难度也会增加。

对于全纯函数，情况则非常不同。这些函数不仅在其定义域中无限可微，而且还具有额外的严格特性，这使得它们难以建模。例如，圆盘中存在全纯函数，它们在圆盘闭合时是连续的，但不能连续(分析地)到比圆盘更大的任何区域。(这个现象在问题 1 中讨论。) 我们在上面看到的另一个事实是，如果全纯函数在小的开集(甚至是非零线段)上消没，则它们必须全为零。

事实证明，本章发展的理论提供了一种在应用中非常有用的简单可拓现象：Schwartz反射原理。证明由两部分组成。首先我们定义扩展，然后检查结果函数是否仍然是全纯的。我们从第二点开始。

令 Ω 为关于实轴对称的 ℂ 的一个开子集，即，

z ∈ Ω 当且仅当 $\overline{z} \in \Omega$ 。

令 $\Omega^{+}$ 表示 Ω 的位于上半平面的部分，令 $\Omega^{-}$ 表示 Ω 的位于下半平面的部分。

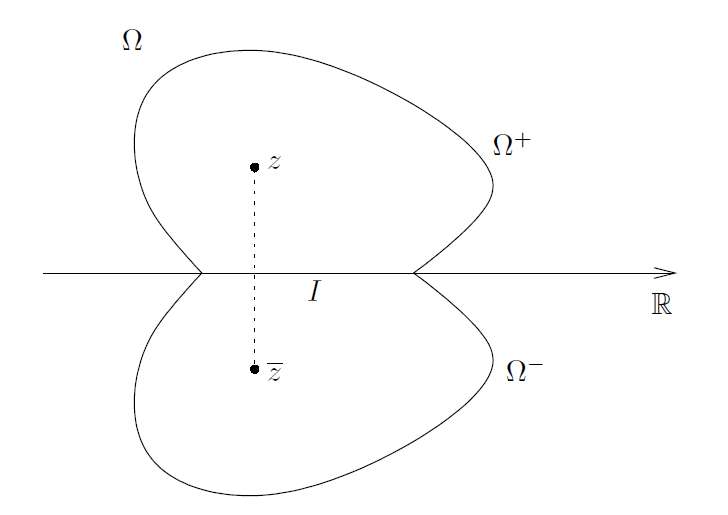
-----------------------------------------------图11：沿实轴对称的开集-----------------------------------------------

此外，令 I = Ω∩ℝ 以使得 I 表示位于实轴上的 $\Omega^{+}$ 和 $\Omega^{-}$ 的边界部分的内部。则我们有

$\Omega^{+} \cup I \cup \Omega^{-} = \Omega$ ，

当然，当 I 非空的时候，下一个定理唯一有趣的情况就发生了。

定理 5.5 (对称原理) 若 $f^{+}$ 和 $f^{-}$ 分别在 $\Omega^{+}$ 和 $\Omega^{-}$ 中是全纯函数，将它们按连续性延拓至I，且对于任意 x ∈ I ，有

$f^{+}(x) = f^{-}(x)$ ，

则按

$f(z)=\left \{ \begin{array}{lc} f^{+}(z)(if \: z{\in} \Omega^{+}) \\ \\ f^{+}(z)=f^{-}(z)(if \: z \in I) \\ \\ f^{-}(z)(if \: z \in \Omega^{-}) \\ \end{array} \right .$

定义在Ω上的函数在整个Ω 上是全纯的。

证明：

读者首先注意到，f 在整个Ω上是连续的。唯一的难点在于证明 f 在I的点上是全纯的。假如 D 是一个圆心位于I上某一点且完全含于Ω的圆盘。我们利用Morera定理可证明 f 在D 中是全纯的。假设T 是D 中的一个三角形。若 T 与 I不相交，则因为f在上下半圆盘中都是全纯的，所以有

$\displaystyle \int_{T}f(z)dz = 0$ 。

现在，假设 T 的一边或一个顶点位含于I中，而T的其余部分含于(比如说)上半圆盘。若三角形 $T_{\epsilon}$ 是通过略稍抬升位于 I 上的一边或一个顶点而获得的，则因为 $T_{\epsilon}$ 完全完于上半圆盘(当一边位于 I 上的这种情况的示意图由图12(a)给出)，则 $\int_{T_{\epsilon}}f = 0$ 。然后，我们令 ε ⟶ 0 ，根据连续性，我们推断出

$\displaystyle \int_{T}f(z)dz = 0$ 。

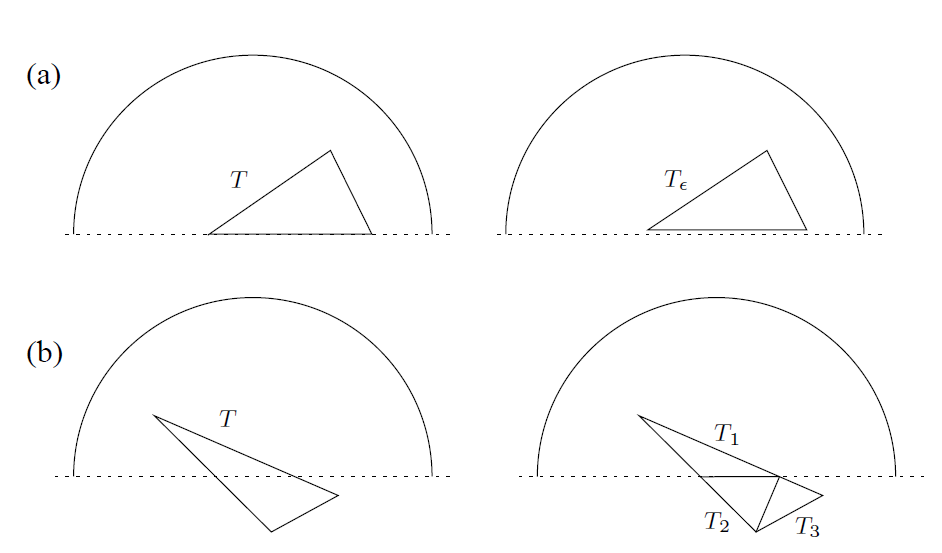
--------------------------------------图12： (a) 抬升一个顶点 (b) 抬升一条边--------------------------------------

若 T 的内部与 I 相交，我们可以通过将 T 写为三角形的并集来将情况简化为前一种情况，每个三角形都有一条边或顶点在 I 上，如图 12(b) 所示。根据Morera定理，我们得出结论，f 在 D 中是全纯的，正如所证。

现在我们表述扩展原理，在其中会用到上述记法。

定理 5.6 (Schwartz 反射原理) 假设 f 是 $\Omega^{+}$ 中的按连续性延拓至 I 且使得f在 I 上是实数值的全纯函数。则存在一个在整个Ω上是全纯的函数 F ，使得在 $\Omega^{+}$ 上有 F = f 。

证明：

证明的思想很简单，对于 $z\in \Omega^{-}$ , 定义 F (z )为

$F (z ) = \overline{f(\overline{z})}$ 。

为了证明 F 在 $\Omega^{-}$ 上是全纯的，我们注意到，若 $z,z_{0} \in \Omega^{-}$ ，则 $\overline{z}, \overline{z_{0}} \in \Omega^{+}$ ,因此，邻近 $\overline{z_{0}}$ 的 f 的幂级数延拓给出

$\displaystyle f(\overline{z})=\sum_{}^{}a_{n}(\overline{z}-\overline{z_{0}})^{n}$ 。

因此，我们看到，

$F(z)=\sum_{}^{}\overline{a_{n}}(z-z_{0})^{n}$ ,

并且F 在 $\Omega^{-}$ 上是全纯的。因为 f 在 I 上是实数值的，只要 x∈I ，我们就有 $\overline{f(x)}=f(x)$ , 因此，F 连续性地延拓至 I 。一旦我们应用对称原理，证明就完成了。

5.5 Runge[rʌndʒ]逼近定理(Runge’s approximation principle)

我们知道，根据Weierstrass定理，一个紧区间(compact interval)(译注：指闭区间)上的任意连续函数都可以使用多项式一致地逼近。带着这样的念头，人们可能会问是否在复分析中也有类似的逼近。更确切地说，我们会提出下面的问题：在某个紧集合 K ⊂ ℂ 上施加什么样的条件才能确保——在这个集合的领域内，任意全纯函数可以用K上的多项式一致地逼近？

这种情况的例子之一便是幂级数展式。我们记得，若f是一个圆盘D上的一个全纯函数，则f 在每一个紧集合 K ⊂ D 上有一个一致地收敛的幂级数展式 $f(z)=\sum_{n=0}^{\infty}a_{n}z^{n}$ 。通过取这个级数的部分和，我们推断出，在D的任意一个紧子集合上，f 可以用多项式一致地逼近(注：其证明见第I册第5章第1.8节)。

然而，在一般情况下，必须在K上施加某种条件，例如，正如我们见过的，在单位圆 K = C 上来考虑函数 $\frac{1}{z}$ 。事实上，我们记得， $\int_{C} f (z)dz = 2\pi{i}$ ，且若p是任意多项式，则根据Cauchy定理，就意味着 $\int_{C} p (z)dz = 0$ ，则很快就导出了矛盾。

在K上的一个确保逼近的约束条件与其补集的拓扑(topology)相关： $K^{c}$ 必须是连通的。事实上，以上例子 $f(z)=\frac{1}{z}$ 略作修改即可证明施于 K上的这个条件是必要的(见问题4)。

反之，若 $K^{c}$ 是连通的，则存在一致逼近，这个结论可以从Runge定理推导出来(Runge定理指出，对于任意的K ，根据具有奇异点(singularities)的比率函数(rational functions)的特性，在 K的补集中，存在函数的一个一致逼近)(注：在这些奇点处，函数不是全纯的，并且是“极点”，如下章所定义)。这个结论是值得注意的，因为比率函数是全局定义的，而 f 仅在 K 的邻域内给出。特别是，f 可以在 K 的不同分量上独立定义，使得该定理的结论更加引人注目。

定理 5.7 在一个紧集合 K 的一个邻域内的任意全纯函数在 K 上可以用其奇异点位于 $K^{c}$ 内的比率函数一致地逼近。

若 $K^{c}$ 是连通的，则K 的一个邻域内的任意全纯函数在K 上都可以用多项式一致地逼近。

我们将看到，定理的第二部分是如何通过第一部分推出的：若 $K^{c}$ 是连通的，人们可以将奇点“推(push)”至无穷大，从而将比率函数转化为多项式。

这个定理的关键在于，积分表示公式是Cauchy积分公式应用于平方的简单结果。

引理 5.8 假设f是一个开集 Ω上的全纯函数，并且 K ⊂ Ω 是紧致的。则在 Ω –K 中存在有限多个段 $r_{1} ,...,r_{N}$ , 使得对于所有 z∈K ，都有

(15) $\displaystyle f(z)=\sum_{n=0}^{\infty}\bigg ( \frac{1}{2\pi{i}} \int_{r_{n}}\frac{f(\zeta)}{\zeta-z}d\zeta\bigg)$ 。

证明：

令 $d = c.d(K, \Omega^{c})$ , 其中，c为任意 < $1/\sqrt{2}$ , 并考虑一个由其边平行于轴且边长为d 的(实线)正方形构成的网格。

我们令 $\mathcal{Q} = \{ Q_{1} , ... , Q_{M} \}$ 网格中与K相交的有限的正方形集，且给定每个正方形的边界为正方向。(我们用 $\partial Q_{m}$ 表示正方形 $Q_{m}$ 的边界。) 最后，我们令 $\gamma_{1},...,\gamma_{M}$ 表示 𝒬 中不属于 𝒬 中两个相邻正方形的正方形的边。(见图13.) 所选择的 d 确保了对于每一个n， $\gamma_{n} \in \Omega$ ，并且 $\gamma_{n}$ 不与 K 相交；因为，若其与K 相交，则会属于 𝒬 中两个相邻正方形，这与我们所选择的 $\gamma_{n}$ 相矛盾。

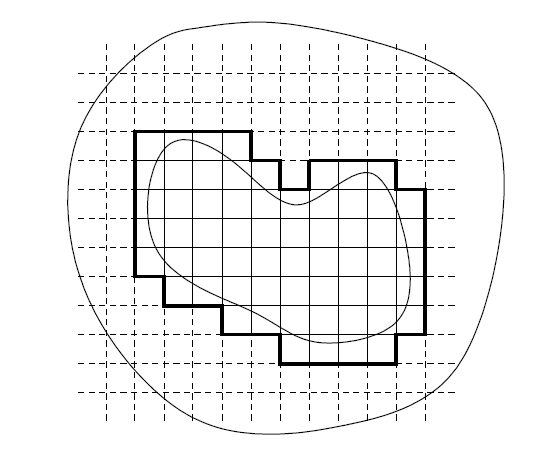
---------------------------------------------图 13: 以粗体表示的 $\gamma_{n}$ ----------------------------------------------------

由于对于不在 𝒬 中一个正方形边界上的任意z∈K ，存在一个j，使得 $z \in Q_{j}$ ，根据Cauchy定理，有

$\displaystyle \frac{1}{2\pi{i}}\int_{\partial {Q_{m}}}\frac{f(\zeta)}{\zeta-z}d\zeta=\left \{ \begin{array}{rlc} f(z)(if \: m=j) \\ \\ 0(if \: m \neq j) \end{array} \right .$ 。

因此，对于所有这样的 z，我们有

$\displaystyle f(z)=\sum_{m=1}^{M} \bigg (\frac{1}{2\pi{i}}\int_{\partial_{Q_{m}}}\frac{f(\zeta)}{\zeta-z}d\zeta \bigg )$ 。

然而，若 $Q_{m}$ 和 $Q_{m^{'}}$ 是相邻的，在它们的公共边上的积分在每个方向积分一次，因此相互抵消。当 z 在 K 中且不在 𝒬 中一个正方形边界上的时候，就确立了 (15) 式。因为 $\gamma_{n}\in \Omega^{c}$ ，连续性确保了这种关系对于所有 z∈K 都成立。引理得证。

因此，定理 5.7 的第一部分是下一个引理的结论。

引理 5.9 对于任意完全含于 Ω –K 中的直线段γ, 存在一系列在γ上具有奇点的比率函数，其在 K 上一致地逼近积分 $\displaystyle \int_{\gamma}\frac{f(\zeta)}{\zeta-z}d\zeta$ 。

证明：

若 γ(t):[0 ,1] ⟶ ℂ 是γ的一个参数化(parametrization)，则

$\displaystyle \int_{\gamma}\frac{f(\zeta)}{\zeta-z}d\zeta=\int_{0}^{1}\frac{f(\gamma(t))}{\gamma(t)-z}\gamma^{'}(t)dt$ 。

因为 γ 与 K 不相交，最后一个积分式中的被积函数 F(z ,t ) 在K × [0 ,1]上是联合连续的，且由于 K 是紧的，任给一个 ε > 0 ，都存在一个δ > 0，使得，只要 $|t_{1}-t_{2}|<\delta$ ，就有

$\displaystyle \sup_{z {\in} {K}}{|F(z,t_{1})-F(z,t_{2})|}<\epsilon$ 。

如定理5.4的证明中的论证，我们可以看到，积分 $\int_{0}^{1}F(z,t)dt$ 的Riemann和在K上一致地逼近它(译注：逼近这个积分)。因为每一个这样的Riemann和在上都是具有奇点的比率函数(rational function)，从而引理得证。

最后，将极点(poles)推向无穷大的这个过程是通过利用 $K^{c}$ 是连通的这个事实完成的。因为任意其唯一奇点位于 $z_{0}$ 点的比率函数都是 $1/(z-z_{0})$ 的一个多项式，这个事实即可建立下述用于完成定理5.7的证明的引理。

引理 5.10 若 $K^{c}$ 是连通的且 $z_{0} \notin K$ ，则函数 $1/(z-z_{0})$ 在K上可以使用多项式一致地逼近。

证明：

首先，我们在一个圆心位于原点且包含K 的大开圆盘D之外选择一个点 $z_{1}$ 。则

$\displaystyle \frac{1}{z-z_{1}}=-\frac{1}{z_{1}}\frac{1}{1-z/z_{1}}=\sum_{n=1}^{\infty}\left ( -\frac{z^{n}}{z_{1}^{n+1}} \right )$ ，

其中，对于 z∈K ，级数一致收敛。级数部分和是多项式，此多项式提供了在K上 $1/(1-z_{1})$ 的一个一致逼近。特别是，这意味着，任意幂 $1/(1-z_{1})^k$ 在K上都可以使用多项式一致地逼近。

现在，完全可证明 $1/(1-z_{0})$ 在 K上可由 $1/(1-z_{1})$ 中的多项式一致地逼近。为了证明，我们利用 $K^{c}$ 从点 $z_{0}$ 到 $z_{1}$ 连通的这个事实。令γ 为 $K^{c}$ 中的一条曲线，并在 [0 ,1] 上用γ(t) 参数化，并使得 $\gamma(0)=z_{0}$ 和 $\gamma(1)=z_{1}$ 。若我们令 $\rho = \frac{1}{2} d(K,\gamma)$ ,则因为γ 和 K 是紧的，所以 ρ > 0 。然后我们选择 γ上的一个点序列 ${ w_{1} ,..., w_{\ell} }$ 并使得 $w_{0} = z_{0} ,w_{\ell} = z_{1}$ ，且对于任意 0 ≤ j < 𝓁 有 $| w_{j }- w_{j+1} | < \rho$ 。

我们断言，若 w 是 γ上的一个点，w’是满足 | w –w’| < ρ 的任意其它点，则 1/(z - w) 在K 上可以由 1/(z - w’)中的多项式一致地逼近。为了理解到这点，请注意

$\displaystyle \frac{1}{z-w}=\frac{1}{1-w^{'}}\frac{1}{\frac{w-w^{'}}{z-w^{'}}}=\sum_{n=0}^{\infty}\left ( \frac{(w-w^{'})^{n}}{(z-w^{'})^{n+1}} \right )$ ，