前缀和个人见解（二）

本文主要是介绍前缀和个人见解（二），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

二维前缀和数组

除了有一维前缀和，也可以推广到 二维。

假设我有一个二维数组，这些红色的点都是数组上的点。

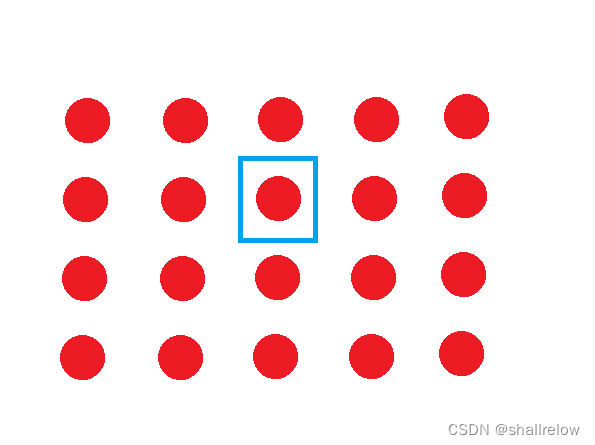
其中用蓝色方框 选中的点 的前缀和 就是 下面的区域的数字之和。

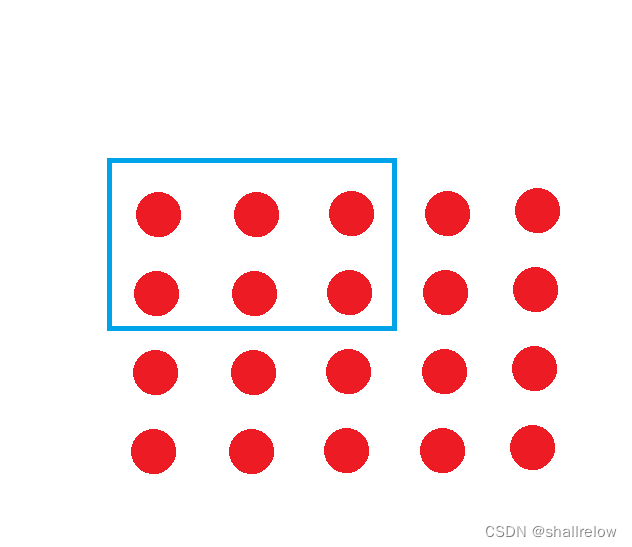
假如是下面的这个点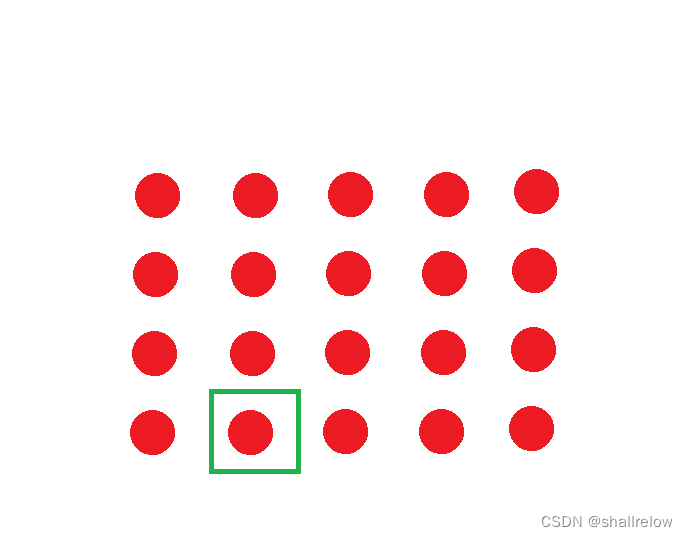

那么它的前缀和就是下面的区域的数字之和。

---

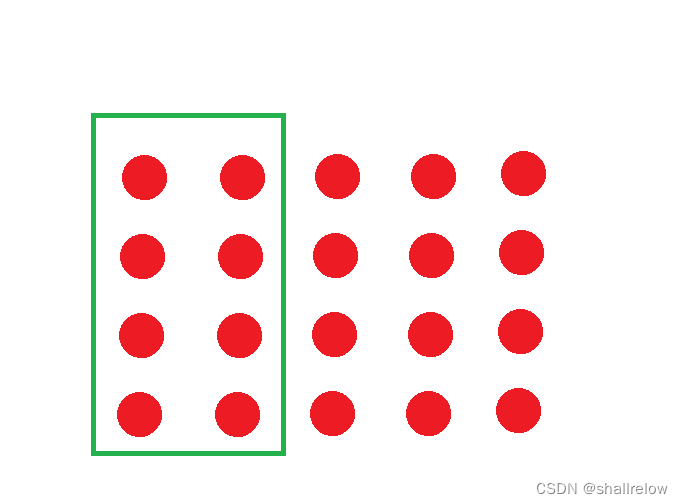
构造二维前缀和数组

接着我们来构造一个二维前缀和数组，也是利用递推的思路。

假设我们要求 紫色这个点的 二维前缀和。

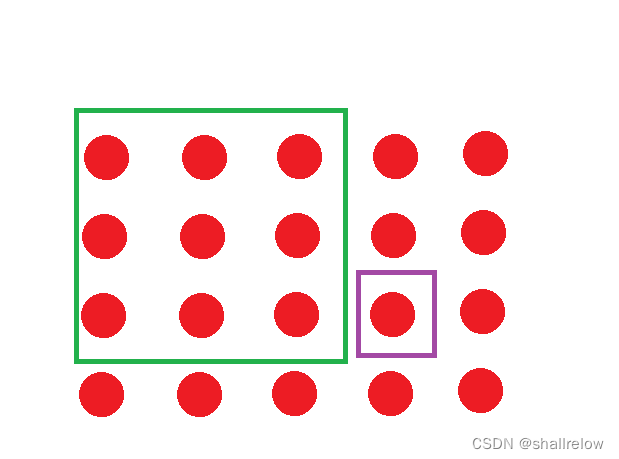
我们可以先加上 这个点左边点的前缀和，也就是 绿色区域内数字之和。

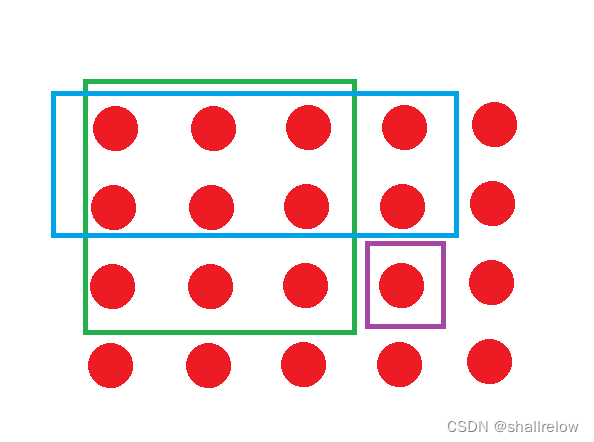
然后再加上 紫色点 的 上边点 的前缀和，也就是 蓝色区域内的 数字之和。

此时会多加了一部分区域，也就是 蓝色和 绿色区域公共的部分，所以需要再减去 紫色点 的左上角点的前缀和。

当然最后得把我们紫色的值也给加上。

如果用代码写的话就是下面的公式。

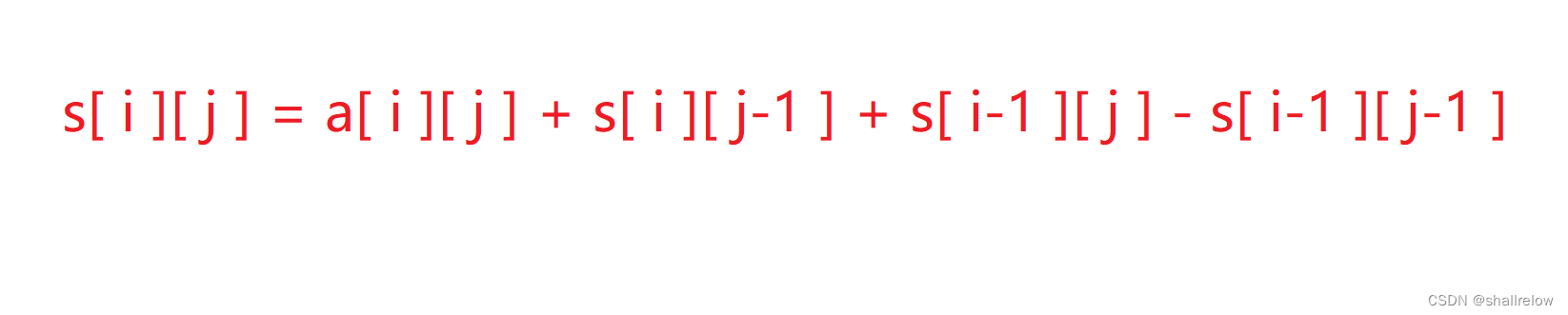
当然 这里的 i 和 j 都不会取到 0，对于前缀和来说，留一层会方便会多。

二维前缀和数组的用途

那么构造了二维前缀和数组之后，它有什么用处呢？

其实跟一维的差不多，一维是求 一个区间内的和，那么二维就是求一个子矩阵的和。

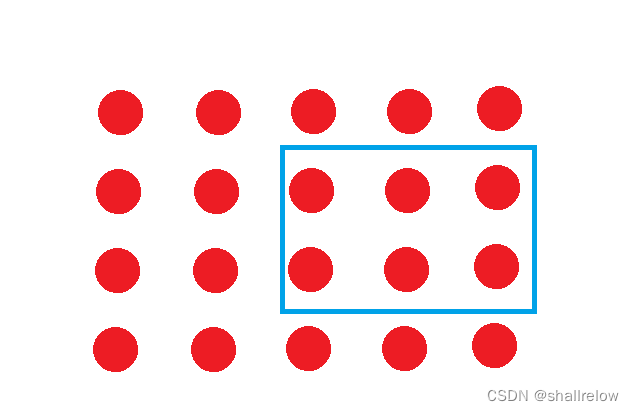
比如我现在让你求这个 蓝色区域内 所有数之和，给你这个矩阵当中的 最左上角点的坐标和 最右下角点的坐标。

此时可以这么计算。

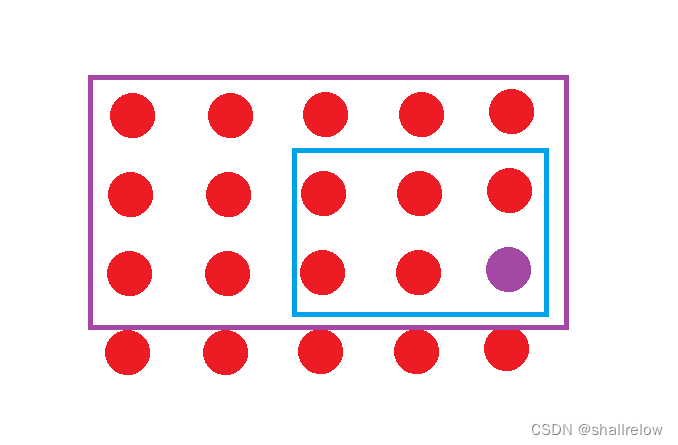
首先先加上 紫色点的前缀和。

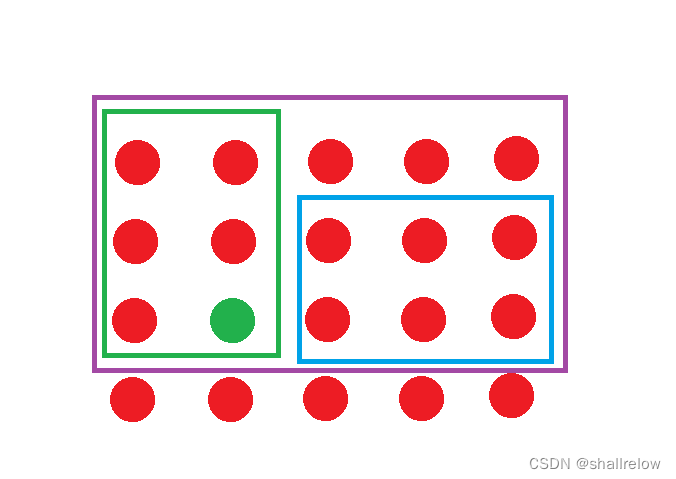
然后减去 绿色点的前缀和。

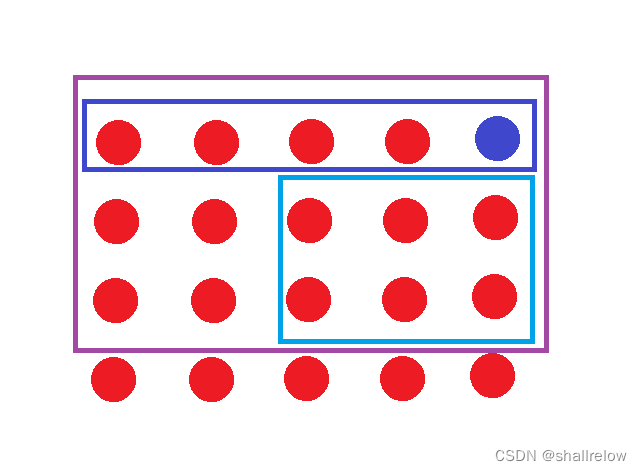
再减去深蓝色的前缀和。

此时 深蓝色和 绿色公共的区域会 减去两次，则需要 再加上该区域，也就是下面 黄色点的前缀和。

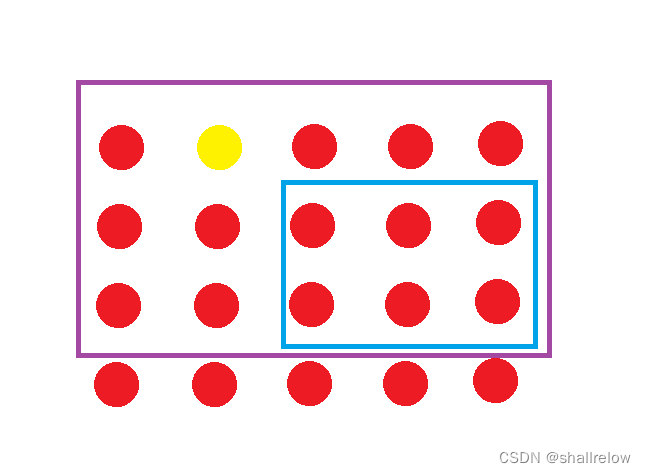
此时 剩余的 就是我们蓝色 区域的 数字之和了。

公式如下：

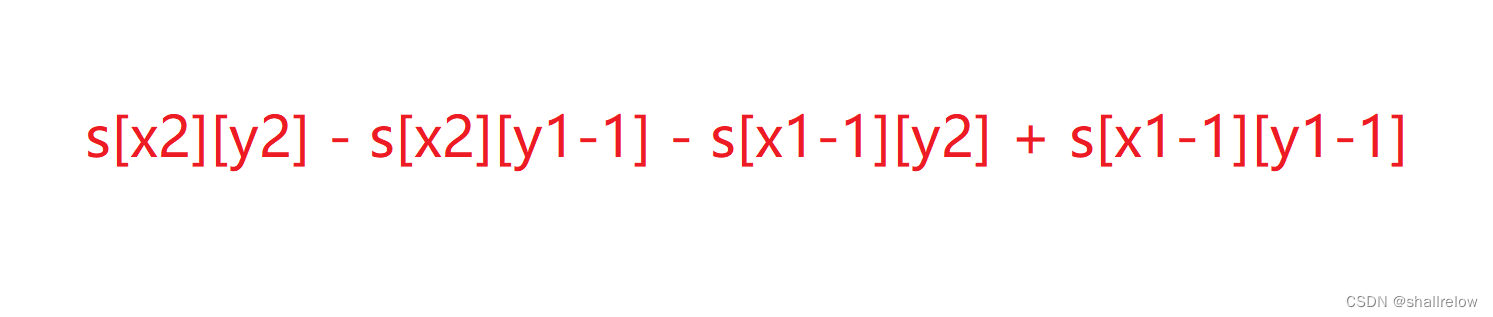
其中 (x1, y1) (x2, y2) 分别为左上角和右下角的点的坐标。

接着我们来一起做做模版题。

题目

输入一个 $n$ 行 $m$ 列的整数矩阵，再输入 $q$ 个询问，每个询问包含四个整数 $x_1,y_1,x_2,y_2$，表示一个子矩阵的左上角坐标和右下角坐标。

对于每个询问输出子矩阵中所有数的和。

输入格式

第一行包含三个整数 $n，m，q$。

接下来 $n$ 行，每行包含 $m$ 个整数，表示整数矩阵。

接下来 $q$ 行，每行包含四个整数 $x_1,y_1,x_2,y_2$，表示一组询问。

输出格式

共 $q$ 行，每行输出一个询问的结果。

数据范围

$1\le n,m\le 1000$,
$1\le q\le 200000$,
$1\le x_1\le x_2\le n$,
$1\le y_1\le y_2\le m$,
$-1000\le 矩阵内元素的值\le 1000$

输入样例：

3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4

输出样例：

17
27
21

准备阶段：

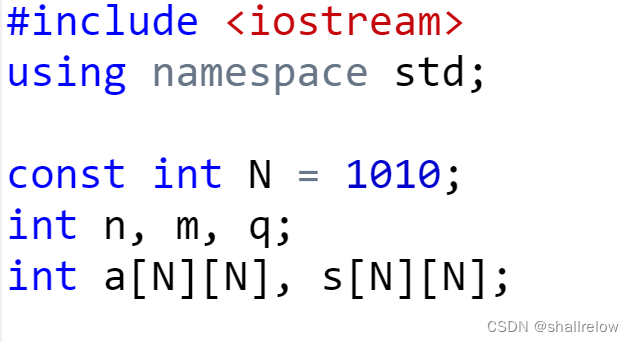
其中 数组 a 存储题目给的原 数据，数组 s 为 a 的 前缀和 数组。

接着写 输入环节，注意是从 1 开始哦，猛猛记住这一点。

之后开始构造我们的 前缀和数组。

这里直接根据公式来就好了，注意公式一定要理解的去背，不能死记硬背。

在写这些公式的时候，你可以自己在脑海里想 区域，这样子会方便记忆公式。

在构造好前缀和数组后，接着就是面临 q 次询问。

对于每次询问，题目会每次给我们两个坐标，然后我们利用 刚才将的公式 直接输出就好啦。

完整代码如下：

#include <iostream>
using namespace std;const int N = 1010;
int n, m, q;
int a[N][N], s[N][N];int main()
{scanf("%d%d%d", &n, &m, &q);for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)scanf("%d", &a[i][j]);for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)s[i][j] = s[i][j-1] + s[i-1][j] - s[i-1][j-1] + a[i][j];while (q--){int x1, y1, x2, y2;scanf("%d%d%d%d", &x1, &y1, &x2, &y2);printf("%d\n", s[x2][y2] - s[x2][y1-1] - s[x1-1][y2] + s[x1-1][y1-1]);}return 0;
}

---

完

这篇关于前缀和个人见解（二）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---