本文主要是介绍笔记99:OSQP 求解器示例代码,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
注1:以下代码是 OSQP 的官方文档提供的示例,我加上了详细的注释;
注2:OSQP 库仅支持C语言,不支持C++,所以下面的示例代码使用的是C语言;但是 OSQP 求解库提供了针对C++的接口 OSQP-EIGEN;
二次规划问题:
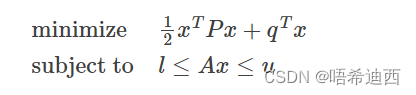

代码:
注:涉及到 csc(按列压缩)的方式表达稀疏矩阵,在文章笔记98:按列压缩矩阵 csc_matrix 的 “含义”-CSDN博客有清晰讲解;
#include <stdlib.h>
#include "osqp.h"int main(int argc, char **argv) {/* 加载问题数据 */// 使用 csc 方式定义矩阵 POSQPFloat P_x[3] = {4.0, 1.0, 2.0, };OSQPInt P_nnz = 3;OSQPInt P_i[3] = {0, 0, 1, };OSQPInt P_p[3] = {0, 1, 3, };// 定义向量 qOSQPFloat q[2] = {1.0, 1.0, };// 使用 csc 方式定义矩阵 AOSQPFloat A_x[4] = {1.0, 1.0, 1.0, 1.0, };OSQPInt A_nnz = 4;OSQPInt A_i[4] = {0, 1, 0, 2, };OSQPInt A_p[3] = {0, 2, 4, };// 定义向量 lOSQPFloat l[3] = {1.0, 0.0, 0.0, };// 定义向量 uOSQPFloat u[3] = {1.0, 0.7, 0.7, };// 状态变量x的维数OSQPInt n = 2;// 约束条件数目OSQPInt m = 3;/* 定义矩阵 *//* 作用:初始化稀疏矩阵 P 和 A *//* OSQPCscMatrix 是 OSQP 中用来表示稀疏矩阵的结构体malloc(sizeof(OSQPCscMatrix)) 分配了足够的内存空间来存储一个 OSQPCscMatrix 结构体实例malloc 函数返回值为一个指向开辟出来的内存空间的指针(如果返回值为 NULL,代表内存分配失败) */OSQPCscMatrix* P = (OSQPCscMatrix*) malloc(sizeof(OSQPCscMatrix));OSQPCscMatrix* A = (OSQPCscMatrix*) malloc(sizeof(OSQPCscMatrix));/* 填充矩阵数据 *//* 注意:csc_set_data 函数是需要用户自定义的,OSQP 库中并未定义这个函数 *//* 作用:根据稀疏矩阵的三个特征数组,来填充得到稀疏矩阵 P 和 A */csc_set_data(A, m, n, A_nnz, A_x, A_i, A_p);csc_set_data(P, n, n, P_nnz, P_x, P_i, P_p);/* 退出标志 *//* 作用:定义退出标志变量,用于检查求解器的状态解 *//* 为0 -- 求解器成功求解为1 -- 问题无解为-1 -- 到达最大迭代次数,问题未能解决 */OSQPInt exitflag = 0;/* 定义求解器,设置 */OSQPSolver *solver; // 指针变量solver -- 指向一个初始化的求解器实例OSQPSettings *settings; // 指针变量settings -- 用于存储求解器的各个设置参数(收敛容差 / 最大迭代次数 ...)/* 初始化 OSQP 求解器的设置参数 */settings = (OSQPSettings *)malloc(sizeof(OSQPSettings)); // 动态分配内存,并将 malloc 函数的返回值强制转化为 OSQPSettings* 类型if (settings) { // 检查内存分配是否成功(是否为 NULL)osqp_set_default_settings(settings); // 用 OSQP 自带的 osqp_set_default_settings 函数初始化 settings 的所有值,均取默认值settings->alpha = 1.0; // 修改 OSQP 求解器的松弛参数}/* 初始化 OSQP 求解器的所有参数 */exitflag = osqp_setup(&solver, P, q, A, l, u, m, n, settings); // 调用 OSQP 自带的 osqp_setup 函数初始化求解器;// 若初始化成功则返回0,若失败则返回非零值;/* 求解问题 */if (!exitflag) exitflag = osqp_solve(solver); // 调用 OSQP 自带的 osqp_solve 函数进行求解/* 访问求解结果 */// 注:osqp_solve 函数的结果会放在 OSQPSolver 结构体的成员变量中;具体来说,OSQPSolver 结构体包含一个指向 OSQPWorkspace 结构体的指针 work,而 OSQPWorkspace 结构体包含求解结果和其他相关信息/* OSQPWorkspace 结构体包含求解器工作区的所有数据,包括求解结果。以下是一些关键成员变量:x: 指向解向量 x 的指针,即优化变量的值;y: 指向对偶变量(拉格朗日乘数)向量 y 的指针;info: 指向 OSQPInfo 结构体的指针,包含有关求解过程的信息(例如迭代次数、状态等); */if (!exitflag) {OSQPFloat *solution = solver->work->solution->x; // 优化变量 xOSQPFloat *dual_vars = solver->work->solution->y; // 对偶变量 y// 输出解向量 xfor (int i = 0; i < 2; i++) { printf("%f\n", solution[i]); }// 输出对偶变量 yfor (int i = 0; i < 3; i++) { printf("%f\n", dual_vars[i]); }}/* 清理内存 */osqp_cleanup(solver);if (A) free(A);if (P) free(P);if (settings) free(settings);return (int)exitflag;
};这篇关于笔记99:OSQP 求解器示例代码的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







