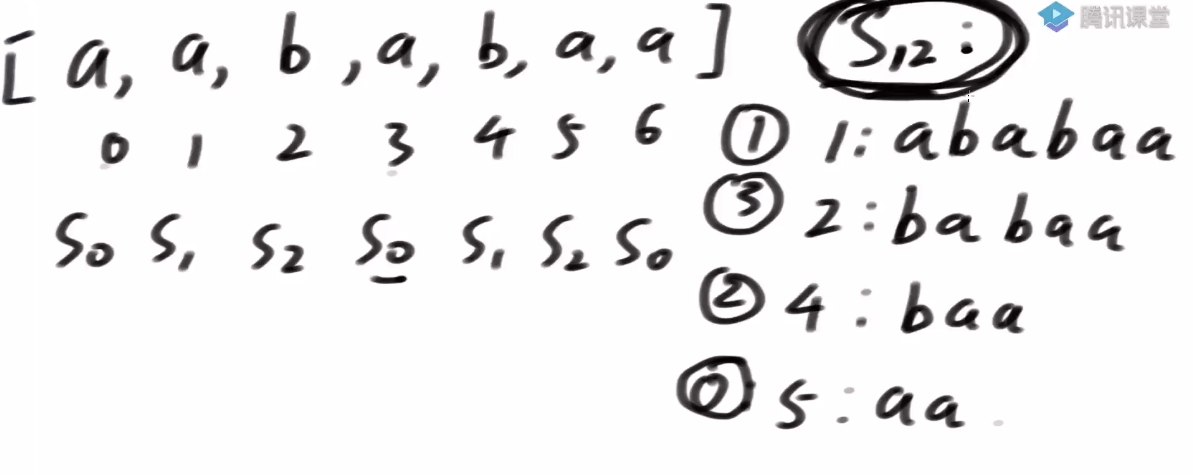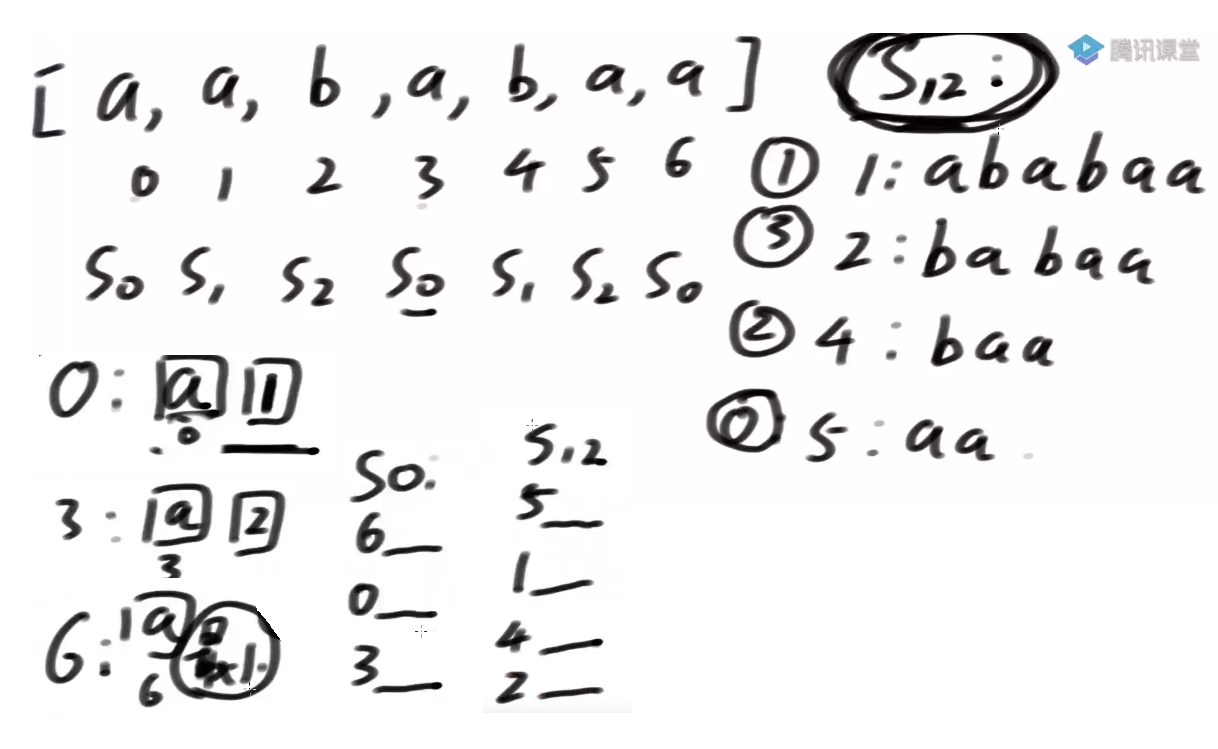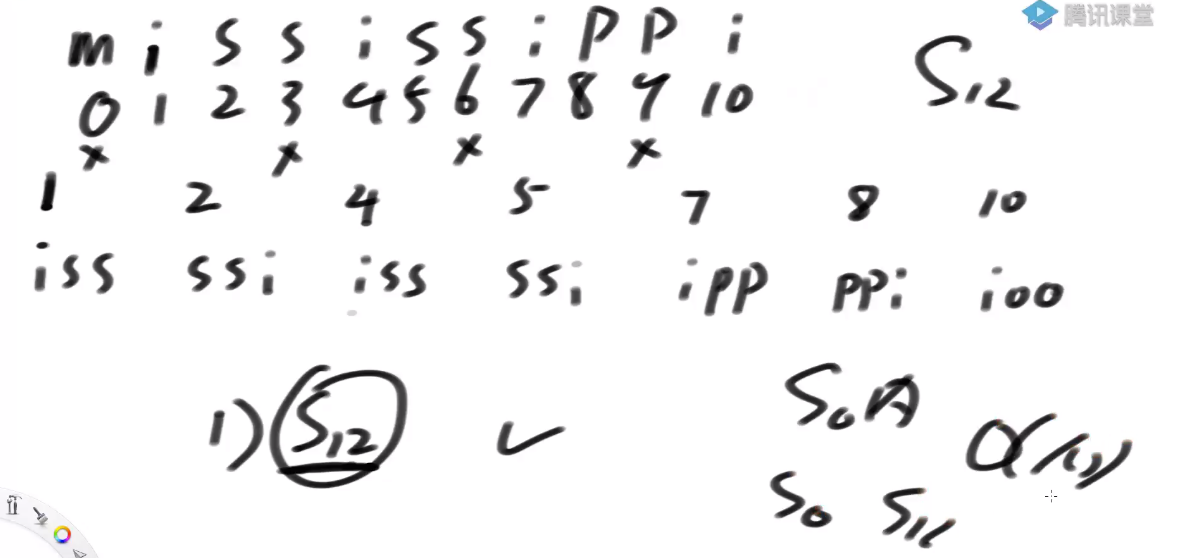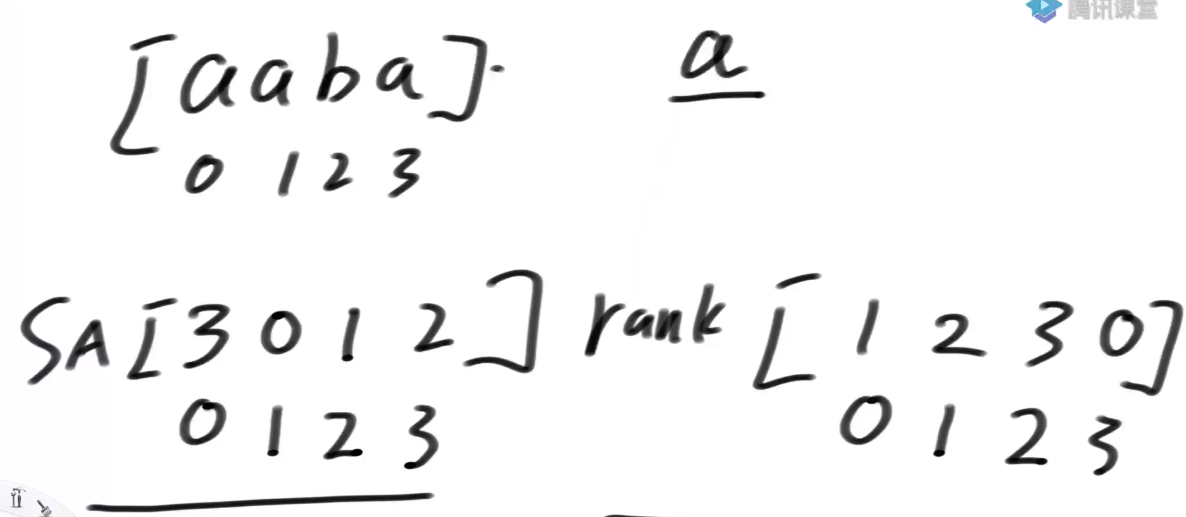本文主要是介绍算法数据结构(三十八)----DC3算法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
后缀和数组
后缀数组其实代表所有的后缀字符串在排完名之后,从第0名到第7名依次写下来,这就是所谓的后缀数组
不会有相同的排名,因为长度不一样
生成后缀数组
1)暴力求解:
先生成所有的后缀字符串,复杂度O(N^2)
后缀字符串数量O(N),N个后缀字符串排序,代价O(N*logN)
2)DC3求解:O(N)
根据下标模3来分组,做了一个类似于递归的事情把这个问题快速解决,有一个前提,初始时,数组里头每个值不要太大,太大的话,常数项就会有点大
DC3步骤
1)首先,做小标分类
i%3==0 ==>0类小标,代号s0
i%3==1 ==>1类小标,代号s1
i%3==2 ==>2类小标,代号s2
2)得到s12类后缀串排名(假设可以得到)
3)当有了s12类的排名后,s0内部的排名过一个基数排序可以直接决定
4)有了s12类排序和s0类排序后,使用一个merge获得整体的排序s012,
先比较6开头和5开头的字符串
s0类跟s2类最多比3回
s0和s1类最多比较2回
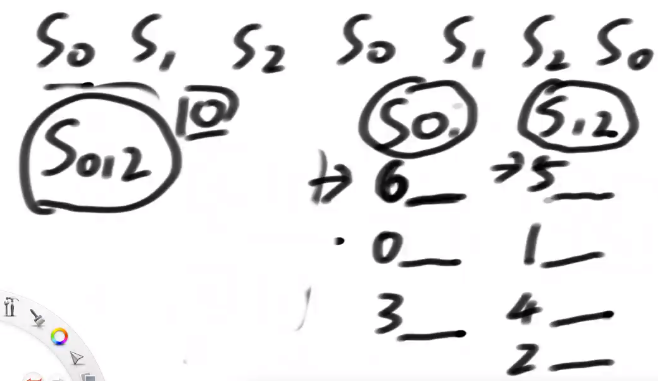


结论:如果我们有s12的排名,我们就可以用O(N)的时间,拿到s0的内部排名,我们还用O(N)的时间merge s012 整体出来的排名,后面的时间都是通过基数排序,最多三类数据,所以s12类排名这个事一旦搞定,这个算法就是O(N)
5)怎么得到s12的排名?
1.只拿前三个字符能得出精确排名吗?
2.如果分不出精确排名
3.组成新数组,s1类放左边,s2类放右边,我缺的就让它挨着
6)DC3算法生成的后缀数组:sa数组 rank数组
public class DC3 {public int[] sa;public int[] rank;public int[] height;// 构造方法的约定:// 数组叫nums,如果你是字符串,请转成整型数组nums// 数组中,最小值>=1// 如果不满足,处理成满足的,也不会影响使用// max, nums里面最大值是多少public DC3(int[] nums, int max) {sa = sa(nums, max);rank = rank();height = height(nums);}private int[] sa(int[] nums, int max) {int n = nums.length;int[] arr = new int[n + 3];for (int i = 0; i < n; i++) {arr[i] = nums[i];}return skew(arr, n, max);}private int[] skew(int[] nums, int n, int K) {int n0 = (n + 2) / 3, n1 = (n + 1) / 3, n2 = n / 3, n02 = n0 + n2;int[] s12 = new int[n02 + 3], sa12 = new int[n02 + 3];for (int i = 0, j = 0; i < n + (n0 - n1); ++i) {if (0 != i % 3) {s12[j++] = i;}}radixPass(nums, s12, sa12, 2, n02, K);radixPass(nums, sa12, s12, 1, n02, K);radixPass(nums, s12, sa12, 0, n02, K);int name = 0, c0 = -1, c1 = -1, c2 = -1;for (int i = 0; i < n02; ++i) {if (c0 != nums[sa12[i]] || c1 != nums[sa12[i] + 1] || c2 != nums[sa12[i] + 2]) {name++;c0 = nums[sa12[i]];c1 = nums[sa12[i] + 1];c2 = nums[sa12[i] + 2];}if (1 == sa12[i] % 3) {s12[sa12[i] / 3] = name;} else {s12[sa12[i] / 3 + n0] = name;}}if (name < n02) {sa12 = skew(s12, n02, name);for (int i = 0; i < n02; i++) {s12[sa12[i]] = i + 1;}} else {for (int i = 0; i < n02; i++) {sa12[s12[i] - 1] = i;}}int[] s0 = new int[n0], sa0 = new int[n0];for (int i = 0, j = 0; i < n02; i++) {if (sa12[i] < n0) {s0[j++] = 3 * sa12[i];}}radixPass(nums, s0, sa0, 0, n0, K);int[] sa = new int[n];for (int p = 0, t = n0 - n1, k = 0; k < n; k++) {int i = sa12[t] < n0 ? sa12[t] * 3 + 1 : (sa12[t] - n0) * 3 + 2;int j = sa0[p];if (sa12[t] < n0 ? leq(nums[i], s12[sa12[t] + n0], nums[j], s12[j / 3]): leq(nums[i], nums[i + 1], s12[sa12[t] - n0 + 1], nums[j], nums[j + 1], s12[j / 3 + n0])) {sa[k] = i;t++;if (t == n02) {for (k++; p < n0; p++, k++) {sa[k] = sa0[p];}}} else {sa[k] = j;p++;if (p == n0) {for (k++; t < n02; t++, k++) {sa[k] = sa12[t] < n0 ? sa12[t] * 3 + 1 : (sa12[t] - n0) * 3 + 2;}}}}return sa;}private void radixPass(int[] nums, int[] input, int[] output, int offset, int n, int k) {int[] cnt = new int[k + 1];for (int i = 0; i < n; ++i) {cnt[nums[input[i] + offset]]++;}for (int i = 0, sum = 0; i < cnt.length; ++i) {int t = cnt[i];cnt[i] = sum;sum += t;}for (int i = 0; i < n; ++i) {output[cnt[nums[input[i] + offset]]++] = input[i];}}private boolean leq(int a1, int a2, int b1, int b2) {return a1 < b1 || (a1 == b1 && a2 <= b2);}private boolean leq(int a1, int a2, int a3, int b1, int b2, int b3) {return a1 < b1 || (a1 == b1 && leq(a2, a3, b2, b3));}private int[] rank() {int n = sa.length;int[] ans = new int[n];for (int i = 0; i < n; i++) {ans[sa[i]] = i;}return ans;}private int[] height(int[] s) {int n = s.length;int[] ans = new int[n];for (int i = 0, k = 0; i < n; ++i) {if (rank[i] != 0) {if (k > 0) {--k;}int j = sa[rank[i] - 1];while (i + k < n && j + k < n && s[i + k] == s[j + k]) {++k;}ans[rank[i]] = k;}}return ans;}// 为了测试public static int[] randomArray(int len, int maxValue) {int[] arr = new int[len];for (int i = 0; i < len; i++) {arr[i] = (int) (Math.random() * maxValue) + 1;}return arr;}// 为了测试public static void main(String[] args) {int len = 100000;int maxValue = 100;long start = System.currentTimeMillis();new DC3(randomArray(len, maxValue), maxValue);long end = System.currentTimeMillis();System.out.println("数据量 " + len + ", 运行时间 " + (end - start) + " ms");}}题目一
https://leetcode.com/problems/last-substring-in-lexicographical-order/
给你一个字符串
s,找出它的所有子串并按字典序排列,返回排在最后的那个子串。利用DC3的sa数组求解
public static String lastSubstring(String s) {if (s == null || s.length() == 0) {return s;}int N = s.length();char[] str = s.toCharArray();int min = Integer.MAX_VALUE;int max = Integer.MIN_VALUE;for (char cha : str) {min = Math.min(min, cha);max = Math.max(max, cha);}int[] arr = new int[N];for (int i = 0; i < N; i++) {arr[i] = str[i] - min + 1;}DC3 dc3 = new DC3(arr, max - min + 1);return s.substring(dc3.sa[N - 1]);}public static class DC3 {public int[] sa;public DC3(int[] nums, int max) {sa = sa(nums, max);}private int[] sa(int[] nums, int max) {int n = nums.length;int[] arr = new int[n + 3];for (int i = 0; i < n; i++) {arr[i] = nums[i];}return skew(arr, n, max);}private int[] skew(int[] nums, int n, int K) {int n0 = (n + 2) / 3, n1 = (n + 1) / 3, n2 = n / 3, n02 = n0 + n2;int[] s12 = new int[n02 + 3], sa12 = new int[n02 + 3];for (int i = 0, j = 0; i < n + (n0 - n1); ++i) {if (0 != i % 3) {s12[j++] = i;}}radixPass(nums, s12, sa12, 2, n02, K);radixPass(nums, sa12, s12, 1, n02, K);radixPass(nums, s12, sa12, 0, n02, K);int name = 0, c0 = -1, c1 = -1, c2 = -1;for (int i = 0; i < n02; ++i) {if (c0 != nums[sa12[i]] || c1 != nums[sa12[i] + 1] || c2 != nums[sa12[i] + 2]) {name++;c0 = nums[sa12[i]];c1 = nums[sa12[i] + 1];c2 = nums[sa12[i] + 2];}if (1 == sa12[i] % 3) {s12[sa12[i] / 3] = name;} else {s12[sa12[i] / 3 + n0] = name;}}if (name < n02) {sa12 = skew(s12, n02, name);for (int i = 0; i < n02; i++) {s12[sa12[i]] = i + 1;}} else {for (int i = 0; i < n02; i++) {sa12[s12[i] - 1] = i;}}int[] s0 = new int[n0], sa0 = new int[n0];for (int i = 0, j = 0; i < n02; i++) {if (sa12[i] < n0) {s0[j++] = 3 * sa12[i];}}radixPass(nums, s0, sa0, 0, n0, K);int[] sa = new int[n];for (int p = 0, t = n0 - n1, k = 0; k < n; k++) {int i = sa12[t] < n0 ? sa12[t] * 3 + 1 : (sa12[t] - n0) * 3 + 2;int j = sa0[p];if (sa12[t] < n0 ? leq(nums[i], s12[sa12[t] + n0], nums[j], s12[j / 3]): leq(nums[i], nums[i + 1], s12[sa12[t] - n0 + 1], nums[j], nums[j + 1], s12[j / 3 + n0])) {sa[k] = i;t++;if (t == n02) {for (k++; p < n0; p++, k++) {sa[k] = sa0[p];}}} else {sa[k] = j;p++;if (p == n0) {for (k++; t < n02; t++, k++) {sa[k] = sa12[t] < n0 ? sa12[t] * 3 + 1 : (sa12[t] - n0) * 3 + 2;}}}}return sa;}private void radixPass(int[] nums, int[] input, int[] output, int offset, int n, int k) {int[] cnt = new int[k + 1];for (int i = 0; i < n; ++i) {cnt[nums[input[i] + offset]]++;}for (int i = 0, sum = 0; i < cnt.length; ++i) {int t = cnt[i];cnt[i] = sum;sum += t;}for (int i = 0; i < n; ++i) {output[cnt[nums[input[i] + offset]]++] = input[i];}}private boolean leq(int a1, int a2, int b1, int b2) {return a1 < b1 || (a1 == b1 && a2 <= b2);}private boolean leq(int a1, int a2, int a3, int b1, int b2, int b3) {return a1 < b1 || (a1 == b1 && leq(a2, a3, b2, b3));}}题目二
给定两个字符串str1和str2,
想把str2整体插入到str1中的某个位置
形成最大的字典序
返回字典序最大的结果
// 暴力方法public static String right(String s1, String s2) {if (s1 == null || s1.length() == 0) {return s2;}if (s2 == null || s2.length() == 0) {return s1;}String p1 = s1 + s2;String p2 = s2 + s1;String ans = p1.compareTo(p2) > 0 ? p1 : p2;for (int end = 1; end < s1.length(); end++) {String cur = s1.substring(0, end) + s2 + s1.substring(end);if (cur.compareTo(ans) > 0) {ans = cur;}}return ans;}// 正式方法 O(N+M) + O(M^2) DC3的rank数组// N : s1长度// M : s2长度public static String maxCombine(String s1, String s2) {if (s1 == null || s1.length() == 0) {return s2;}if (s2 == null || s2.length() == 0) {return s1;}char[] str1 = s1.toCharArray();char[] str2 = s2.toCharArray();int N = str1.length;int M = str2.length;int min = str1[0];int max = str1[0];for (int i = 1; i < N; i++) {min = Math.min(min, str1[i]);max = Math.max(max, str1[i]);}for (int i = 0; i < M; i++) {min = Math.min(min, str2[i]);max = Math.max(max, str2[i]);}int[] all = new int[N + M + 1];int index = 0;for (int i = 0; i < N; i++) {all[index++] = str1[i] - min + 2;}all[index++] = 1;for (int i = 0; i < M; i++) {all[index++] = str2[i] - min + 2;}DC3 dc3 = new DC3(all, max - min + 2);int[] rank = dc3.rank;int comp = N + 1;for (int i = 0; i < N; i++) {if (rank[i] < rank[comp]) {int best = bestSplit(s1, s2, i);return s1.substring(0, best) + s2 + s1.substring(best);}}return s1 + s2;}public static int bestSplit(String s1, String s2, int first) {int N = s1.length();int M = s2.length();int end = N;for (int i = first, j = 0; i < N && j < M; i++, j++) {if (s1.charAt(i) < s2.charAt(j)) {end = i;break;}}String bestPrefix = s2;int bestSplit = first;for (int i = first + 1, j = M - 1; i <= end; i++, j--) {String curPrefix = s1.substring(first, i) + s2.substring(0, j);if (curPrefix.compareTo(bestPrefix) >= 0) {bestPrefix = curPrefix;bestSplit = i;}}return bestSplit;}public static class DC3 {public int[] sa;public int[] rank;public DC3(int[] nums, int max) {sa = sa(nums, max);rank = rank();}private int[] sa(int[] nums, int max) {int n = nums.length;int[] arr = new int[n + 3];for (int i = 0; i < n; i++) {arr[i] = nums[i];}return skew(arr, n, max);}private int[] skew(int[] nums, int n, int K) {int n0 = (n + 2) / 3, n1 = (n + 1) / 3, n2 = n / 3, n02 = n0 + n2;int[] s12 = new int[n02 + 3], sa12 = new int[n02 + 3];for (int i = 0, j = 0; i < n + (n0 - n1); ++i) {if (0 != i % 3) {s12[j++] = i;}}radixPass(nums, s12, sa12, 2, n02, K);radixPass(nums, sa12, s12, 1, n02, K);radixPass(nums, s12, sa12, 0, n02, K);int name = 0, c0 = -1, c1 = -1, c2 = -1;for (int i = 0; i < n02; ++i) {if (c0 != nums[sa12[i]] || c1 != nums[sa12[i] + 1] || c2 != nums[sa12[i] + 2]) {name++;c0 = nums[sa12[i]];c1 = nums[sa12[i] + 1];c2 = nums[sa12[i] + 2];}if (1 == sa12[i] % 3) {s12[sa12[i] / 3] = name;} else {s12[sa12[i] / 3 + n0] = name;}}if (name < n02) {sa12 = skew(s12, n02, name);for (int i = 0; i < n02; i++) {s12[sa12[i]] = i + 1;}} else {for (int i = 0; i < n02; i++) {sa12[s12[i] - 1] = i;}}int[] s0 = new int[n0], sa0 = new int[n0];for (int i = 0, j = 0; i < n02; i++) {if (sa12[i] < n0) {s0[j++] = 3 * sa12[i];}}radixPass(nums, s0, sa0, 0, n0, K);int[] sa = new int[n];for (int p = 0, t = n0 - n1, k = 0; k < n; k++) {int i = sa12[t] < n0 ? sa12[t] * 3 + 1 : (sa12[t] - n0) * 3 + 2;int j = sa0[p];if (sa12[t] < n0 ? leq(nums[i], s12[sa12[t] + n0], nums[j], s12[j / 3]): leq(nums[i], nums[i + 1], s12[sa12[t] - n0 + 1], nums[j], nums[j + 1], s12[j / 3 + n0])) {sa[k] = i;t++;if (t == n02) {for (k++; p < n0; p++, k++) {sa[k] = sa0[p];}}} else {sa[k] = j;p++;if (p == n0) {for (k++; t < n02; t++, k++) {sa[k] = sa12[t] < n0 ? sa12[t] * 3 + 1 : (sa12[t] - n0) * 3 + 2;}}}}return sa;}private void radixPass(int[] nums, int[] input, int[] output, int offset, int n, int k) {int[] cnt = new int[k + 1];for (int i = 0; i < n; ++i) {cnt[nums[input[i] + offset]]++;}for (int i = 0, sum = 0; i < cnt.length; ++i) {int t = cnt[i];cnt[i] = sum;sum += t;}for (int i = 0; i < n; ++i) {output[cnt[nums[input[i] + offset]]++] = input[i];}}private boolean leq(int a1, int a2, int b1, int b2) {return a1 < b1 || (a1 == b1 && a2 <= b2);}private boolean leq(int a1, int a2, int a3, int b1, int b2, int b3) {return a1 < b1 || (a1 == b1 && leq(a2, a3, b2, b3));}private int[] rank() {int n = sa.length;int[] ans = new int[n];for (int i = 0; i < n; i++) {ans[sa[i]] = i;}return ans;}}
题目三
https://leetcode.com/problems/create-maximum-number/
给两个长度分别为M和N的整型数组nums1和nums2,其中每个值都不大于9,再给定一个正数K。 你可以在nums1和nums2中挑选数字,要求一共挑选K个,并且要从左到右挑。返回所有可能的结果中,代表最大数字的结果。
public static int[] maxNumber1(int[] nums1, int[] nums2, int k) {int len1 = nums1.length;int len2 = nums2.length;if (k < 0 || k > len1 + len2) {return null;}int[] res = new int[k];int[][] dp1 = getdp(nums1); // 生成dp1这个表,以后从nums1中,只要固定拿N个数,int[][] dp2 = getdp(nums2);// get1 从arr1里拿的数量// K - get1 从arr2里拿的数量for (int get1 = Math.max(0, k - len2); get1 <= Math.min(k, len1); get1++) {// arr1 挑 get1个,怎么得到一个最优结果int[] pick1 = maxPick(nums1, dp1, get1);int[] pick2 = maxPick(nums2, dp2, k - get1);int[] merge = merge(pick1, pick2);res = preMoreThanLast(res, 0, merge, 0) ? res : merge;}return res;}public static int[] merge(int[] nums1, int[] nums2) {int k = nums1.length + nums2.length;int[] ans = new int[k];for (int i = 0, j = 0, r = 0; r < k; ++r) {ans[r] = preMoreThanLast(nums1, i, nums2, j) ? nums1[i++] : nums2[j++];}return ans;}public static boolean preMoreThanLast(int[] nums1, int i, int[] nums2, int j) {while (i < nums1.length && j < nums2.length && nums1[i] == nums2[j]) {i++;j++;}return j == nums2.length || (i < nums1.length && nums1[i] > nums2[j]);}public static int[][] getdp(int[] arr) {int size = arr.length; // 0~N-1int pick = arr.length + 1; // 1 ~ Nint[][] dp = new int[size][pick];// get 不从0开始,因为拿0个无意义for (int get = 1; get < pick; get++) { // 1 ~ Nint maxIndex = size - get;// i~N-1for (int i = size - get; i >= 0; i--) {if (arr[i] >= arr[maxIndex]) {maxIndex = i;}dp[i][get] = maxIndex;}}return dp;}public static int[] maxPick(int[] arr, int[][] dp, int pick) {int[] res = new int[pick];for (int resIndex = 0, dpRow = 0; pick > 0; pick--, resIndex++) {res[resIndex] = arr[dp[dpRow][pick]];dpRow = dp[dpRow][pick] + 1;}return res;}public static int[] maxNumber2(int[] nums1, int[] nums2, int k) {int len1 = nums1.length;int len2 = nums2.length;if (k < 0 || k > len1 + len2) {return null;}int[] res = new int[k];int[][] dp1 = getdp(nums1);int[][] dp2 = getdp(nums2);for (int get1 = Math.max(0, k - len2); get1 <= Math.min(k, len1); get1++) {int[] pick1 = maxPick(nums1, dp1, get1);int[] pick2 = maxPick(nums2, dp2, k - get1);int[] merge = mergeBySuffixArray(pick1, pick2);res = moreThan(res, merge) ? res : merge;}return res;}public static boolean moreThan(int[] pre, int[] last) {int i = 0;int j = 0;while (i < pre.length && j < last.length && pre[i] == last[j]) {i++;j++;}return j == last.length || (i < pre.length && pre[i] > last[j]);}public static int[] mergeBySuffixArray(int[] nums1, int[] nums2) {int size1 = nums1.length;int size2 = nums2.length;int[] nums = new int[size1 + 1 + size2];for (int i = 0; i < size1; i++) {nums[i] = nums1[i] + 2;}nums[size1] = 1;for (int j = 0; j < size2; j++) {nums[j + size1 + 1] = nums2[j] + 2;}DC3 dc3 = new DC3(nums, 11);int[] rank = dc3.rank;int[] ans = new int[size1 + size2];int i = 0;int j = 0;int r = 0;while (i < size1 && j < size2) {ans[r++] = rank[i] > rank[j + size1 + 1] ? nums1[i++] : nums2[j++];}while (i < size1) {ans[r++] = nums1[i++];}while (j < size2) {ans[r++] = nums2[j++];}return ans;}public static class DC3 {public int[] sa;public int[] rank;public DC3(int[] nums, int max) {sa = sa(nums, max);rank = rank();}private int[] sa(int[] nums, int max) {int n = nums.length;int[] arr = new int[n + 3];for (int i = 0; i < n; i++) {arr[i] = nums[i];}return skew(arr, n, max);}private int[] skew(int[] nums, int n, int K) {int n0 = (n + 2) / 3, n1 = (n + 1) / 3, n2 = n / 3, n02 = n0 + n2;int[] s12 = new int[n02 + 3], sa12 = new int[n02 + 3];for (int i = 0, j = 0; i < n + (n0 - n1); ++i) {if (0 != i % 3) {s12[j++] = i;}}radixPass(nums, s12, sa12, 2, n02, K);radixPass(nums, sa12, s12, 1, n02, K);radixPass(nums, s12, sa12, 0, n02, K);int name = 0, c0 = -1, c1 = -1, c2 = -1;for (int i = 0; i < n02; ++i) {if (c0 != nums[sa12[i]] || c1 != nums[sa12[i] + 1] || c2 != nums[sa12[i] + 2]) {name++;c0 = nums[sa12[i]];c1 = nums[sa12[i] + 1];c2 = nums[sa12[i] + 2];}if (1 == sa12[i] % 3) {s12[sa12[i] / 3] = name;} else {s12[sa12[i] / 3 + n0] = name;}}if (name < n02) {sa12 = skew(s12, n02, name);for (int i = 0; i < n02; i++) {s12[sa12[i]] = i + 1;}} else {for (int i = 0; i < n02; i++) {sa12[s12[i] - 1] = i;}}int[] s0 = new int[n0], sa0 = new int[n0];for (int i = 0, j = 0; i < n02; i++) {if (sa12[i] < n0) {s0[j++] = 3 * sa12[i];}}radixPass(nums, s0, sa0, 0, n0, K);int[] sa = new int[n];for (int p = 0, t = n0 - n1, k = 0; k < n; k++) {int i = sa12[t] < n0 ? sa12[t] * 3 + 1 : (sa12[t] - n0) * 3 + 2;int j = sa0[p];if (sa12[t] < n0 ? leq(nums[i], s12[sa12[t] + n0], nums[j], s12[j / 3]): leq(nums[i], nums[i + 1], s12[sa12[t] - n0 + 1], nums[j], nums[j + 1], s12[j / 3 + n0])) {sa[k] = i;t++;if (t == n02) {for (k++; p < n0; p++, k++) {sa[k] = sa0[p];}}} else {sa[k] = j;p++;if (p == n0) {for (k++; t < n02; t++, k++) {sa[k] = sa12[t] < n0 ? sa12[t] * 3 + 1 : (sa12[t] - n0) * 3 + 2;}}}}return sa;}private void radixPass(int[] nums, int[] input, int[] output, int offset, int n, int k) {int[] cnt = new int[k + 1];for (int i = 0; i < n; ++i) {cnt[nums[input[i] + offset]]++;}for (int i = 0, sum = 0; i < cnt.length; ++i) {int t = cnt[i];cnt[i] = sum;sum += t;}for (int i = 0; i < n; ++i) {output[cnt[nums[input[i] + offset]]++] = input[i];}}private boolean leq(int a1, int a2, int b1, int b2) {return a1 < b1 || (a1 == b1 && a2 <= b2);}private boolean leq(int a1, int a2, int a3, int b1, int b2, int b3) {return a1 < b1 || (a1 == b1 && leq(a2, a3, b2, b3));}private int[] rank() {int n = sa.length;int[] ans = new int[n];for (int i = 0; i < n; i++) {ans[sa[i]] = i;}return ans;}}public static int[][] getdp(int[] arr) {int size = arr.length; // 0~N-1int pick = arr.length + 1; // 1 ~ Nint[][] dp = new int[size][pick];// get 不从0开始,因为拿0个无意义for (int get = 1; get < pick; get++) { // 1 ~ Nint maxIndex = size - get;// i~N-1for (int i = size - get; i >= 0; i--) {if (arr[i] >= arr[maxIndex]) {maxIndex = i;}dp[i][get] = maxIndex;}}return dp;}public static int[] maxPick(int[] arr, int[][] dp, int pick) {int[] res = new int[pick];for (int resIndex = 0, dpRow = 0; pick > 0; pick--, resIndex++) {res[resIndex] = arr[dp[dpRow][pick]];dpRow = dp[dpRow][pick] + 1;}return res;}题目四
最长公共子串问题是面试常见题目之一,假设str1长度N,str2长度M
一般在面试场上回答出O(N*M)的解法已经是比较优秀了
因为得到O(N*M)的解法,就已经需要用到动态规划了
但其实这个问题的最优解是O(N+M),需要用到后缀数组+height数组
height数组:height[i]指在sa中第i名的和第i-1名的最长公共前缀
public static int lcs1(String s1, String s2) {if (s1 == null || s2 == null || s1.length() == 0 || s2.length() == 0) {return 0;}char[] str1 = s1.toCharArray();char[] str2 = s2.toCharArray();int row = 0;int col = str2.length - 1;int max = 0;while (row < str1.length) {int i = row;int j = col;int len = 0;while (i < str1.length && j < str2.length) {if (str1[i] != str2[j]) {len = 0;} else {len++;}if (len > max) {max = len;}i++;j++;}if (col > 0) {col--;} else {row++;}}return max;}// 最长公共子串问题是面试常见题目之一
// 假设str1长度N,str2长度M
// 因为最优解的难度所限,一般在面试场上回答出O(N*M)的解法已经是比较优秀了
// 因为得到O(N*M)的解法,就已经需要用到动态规划了
// 但其实这个问题的最优解是O(N+M),为了达到这个复杂度可是不容易
// 首先需要用到DC3算法得到后缀数组(sa)
// 进而用sa数组去生成height数组
// 而且在生成的时候,还有一个不回退的优化,都非常不容易理解
// 这就是后缀数组在面试算法中的地位 : 德高望重的噩梦
public static int lcs2(String s1, String s2) {if (s1 == null || s2 == null || s1.length() == 0 || s2.length() == 0) {return 0;}char[] str1 = s1.toCharArray();char[] str2 = s2.toCharArray();int N = str1.length;int M = str2.length;int min = str1[0];int max = str1[0];for (int i = 1; i < N; i++) {min = Math.min(min, str1[i]);max = Math.max(max, str1[i]);}for (int i = 0; i < M; i++) {min = Math.min(min, str2[i]);max = Math.max(max, str2[i]);}int[] all = new int[N + M + 1];int index = 0;for (int i = 0; i < N; i++) {all[index++] = str1[i] - min + 2;}all[index++] = 1;for (int i = 0; i < M; i++) {all[index++] = str2[i] - min + 2;}DC3 dc3 = new DC3(all, max - min + 2);int n = all.length;int[] sa = dc3.sa;int[] height = dc3.height;int ans = 0;for (int i = 1; i < n; i++) {int Y = sa[i - 1];int X = sa[i];if (Math.min(X, Y) < N && Math.max(X, Y) > N) {ans = Math.max(ans, height[i]);}}return ans;}public static class DC3 {public int[] sa;public int[] rank;public int[] height;public DC3(int[] nums, int max) {sa = sa(nums, max);rank = rank();height = height(nums);}private int[] sa(int[] nums, int max) {int n = nums.length;int[] arr = new int[n + 3];for (int i = 0; i < n; i++) {arr[i] = nums[i];}return skew(arr, n, max);}private int[] skew(int[] nums, int n, int K) {int n0 = (n + 2) / 3, n1 = (n + 1) / 3, n2 = n / 3, n02 = n0 + n2;int[] s12 = new int[n02 + 3], sa12 = new int[n02 + 3];for (int i = 0, j = 0; i < n + (n0 - n1); ++i) {if (0 != i % 3) {s12[j++] = i;}}radixPass(nums, s12, sa12, 2, n02, K);radixPass(nums, sa12, s12, 1, n02, K);radixPass(nums, s12, sa12, 0, n02, K);int name = 0, c0 = -1, c1 = -1, c2 = -1;for (int i = 0; i < n02; ++i) {if (c0 != nums[sa12[i]] || c1 != nums[sa12[i] + 1] || c2 != nums[sa12[i] + 2]) {name++;c0 = nums[sa12[i]];c1 = nums[sa12[i] + 1];c2 = nums[sa12[i] + 2];}if (1 == sa12[i] % 3) {s12[sa12[i] / 3] = name;} else {s12[sa12[i] / 3 + n0] = name;}}if (name < n02) {sa12 = skew(s12, n02, name);for (int i = 0; i < n02; i++) {s12[sa12[i]] = i + 1;}} else {for (int i = 0; i < n02; i++) {sa12[s12[i] - 1] = i;}}int[] s0 = new int[n0], sa0 = new int[n0];for (int i = 0, j = 0; i < n02; i++) {if (sa12[i] < n0) {s0[j++] = 3 * sa12[i];}}radixPass(nums, s0, sa0, 0, n0, K);int[] sa = new int[n];for (int p = 0, t = n0 - n1, k = 0; k < n; k++) {int i = sa12[t] < n0 ? sa12[t] * 3 + 1 : (sa12[t] - n0) * 3 + 2;int j = sa0[p];if (sa12[t] < n0 ? leq(nums[i], s12[sa12[t] + n0], nums[j], s12[j / 3]): leq(nums[i], nums[i + 1], s12[sa12[t] - n0 + 1], nums[j], nums[j + 1], s12[j / 3 + n0])) {sa[k] = i;t++;if (t == n02) {for (k++; p < n0; p++, k++) {sa[k] = sa0[p];}}} else {sa[k] = j;p++;if (p == n0) {for (k++; t < n02; t++, k++) {sa[k] = sa12[t] < n0 ? sa12[t] * 3 + 1 : (sa12[t] - n0) * 3 + 2;}}}}return sa;}private void radixPass(int[] nums, int[] input, int[] output, int offset, int n, int k) {int[] cnt = new int[k + 1];for (int i = 0; i < n; ++i) {cnt[nums[input[i] + offset]]++;}for (int i = 0, sum = 0; i < cnt.length; ++i) {int t = cnt[i];cnt[i] = sum;sum += t;}for (int i = 0; i < n; ++i) {output[cnt[nums[input[i] + offset]]++] = input[i];}}private boolean leq(int a1, int a2, int b1, int b2) {return a1 < b1 || (a1 == b1 && a2 <= b2);}private boolean leq(int a1, int a2, int a3, int b1, int b2, int b3) {return a1 < b1 || (a1 == b1 && leq(a2, a3, b2, b3));}private int[] rank() {int n = sa.length;int[] ans = new int[n];for (int i = 0; i < n; i++) {ans[sa[i]] = i;}return ans;}private int[] height(int[] s) {int n = s.length;int[] ans = new int[n];// 依次求h[i] , k = 0for (int i = 0, k = 0; i < n; ++i) {if (rank[i] != 0) {if (k > 0) {--k;}int j = sa[rank[i] - 1];while (i + k < n && j + k < n && s[i + k] == s[j + k]) {++k;}// h[i] = kans[rank[i]] = k;}}return ans;}}这篇关于算法数据结构(三十八)----DC3算法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!