本文主要是介绍算法数据结构(三十五)----子数组达到累加和的最大长度系列,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题目一
给定一个正整数组成的无序数组arr,给定一个正整数值K
找到arr的所有子数组里,哪个子数组的累加和等于K,并且是长度最大的
返回其长度
//滑动窗口
public static int getMaxLength(int[] arr, int K) {if (arr == null || arr.length == 0 || K <= 0) {return 0;}int left = 0;int right = 0;int sum = arr[0];int len = 0;while (right < arr.length) {if (sum == K) {len = Math.max(len, right - left + 1);sum -= arr[left++];} else if (sum < K) {right++;if (right == arr.length) {break;}sum += arr[right];} else {sum -= arr[left++];}}return len;}题目二
给定一个整数组成的无序数组arr,值可能正、可能负、可能0
给定一个整数值K
找到arr的所有子数组里,哪个子数组的累加和等于K,并且是长度最大的
返回其长度
//使用前缀和预处理数据
public static int maxLength(int[] arr, int k) {if (arr == null || arr.length == 0) {return 0;}// key:前缀和// value : 0~value这个前缀和是最早出现key这个值的HashMap<Integer, Integer> map = new HashMap<Integer, Integer>();map.put(0, -1); // importantint len = 0;int sum = 0;for (int i = 0; i < arr.length; i++) {sum += arr[i];if (map.containsKey(sum - k)) {len = Math.max(i - map.get(sum - k), len);}if (!map.containsKey(sum)) {map.put(sum, i);}}return len;}题目三
给定一个整数组成的无序数组arr,值可能正、可能负、可能0
给定一个整数值K
找到arr的所有子数组里,哪个子数组的累加和<=K,并且是长度最大的
返回其长度
public static int maxLengthAwesome(int[] arr, int k) {if (arr == null || arr.length == 0) {return 0;}int[] minSums = new int[arr.length];int[] minSumEnds = new int[arr.length];minSums[arr.length - 1] = arr[arr.length - 1];minSumEnds[arr.length - 1] = arr.length - 1;for (int i = arr.length - 2; i >= 0; i--) {if (minSums[i + 1] < 0) {minSums[i] = arr[i] + minSums[i + 1];minSumEnds[i] = minSumEnds[i + 1];} else {minSums[i] = arr[i];minSumEnds[i] = i;}}// 迟迟扩不进来那一块儿的开头位置int end = 0;int sum = 0;int ans = 0;for (int i = 0; i < arr.length; i++) {// while循环结束之后:// 1) 如果以i开头的情况下,累加和<=k的最长子数组是arr[i..end-1],看看这个子数组长度能不能更新res;// 2) 如果以i开头的情况下,累加和<=k的最长子数组比arr[i..end-1]短,更新还是不更新res都不会影响最终结果;while (end < arr.length && sum + minSums[end] <= k) {sum += minSums[end];end = minSumEnds[end] + 1;}ans = Math.max(ans, end - i);if (end > i) { // 还有窗口,哪怕窗口没有数字 [i~end) [4,4)sum -= arr[i];} else { // i == end, 即将 i++, i > end, 此时窗口概念维持不住了,所以end跟着i一起走end = i + 1;}}return ans;}题目四
给定一个数组arr,给定一个值v
求子数组平均值小于等于v的最长子数组长度
// 暴力解,时间复杂度O(N^3),用于做对数器public static int ways1(int[] arr, int v) {int ans = 0;for (int L = 0; L < arr.length; L++) {for (int R = L; R < arr.length; R++) {int sum = 0;int k = R - L + 1;for (int i = L; i <= R; i++) {sum += arr[i];}double avg = (double) sum / (double) k;if (avg <= v) {ans = Math.max(ans, k);}}}return ans;}// 想实现的解法2,时间复杂度O(N*logN)public static int ways2(int[] arr, int v) {if (arr == null || arr.length == 0) {return 0;}TreeMap<Integer, Integer> origins = new TreeMap<>();int ans = 0;int modify = 0;for (int i = 0; i < arr.length; i++) {int p1 = arr[i] <= v ? 1 : 0;int p2 = 0;int querry = -arr[i] - modify;if (origins.floorKey(querry) != null) {p2 = i - origins.get(origins.floorKey(querry)) + 1;}ans = Math.max(ans, Math.max(p1, p2));int curOrigin = -modify - v;if (origins.floorKey(curOrigin) == null) {origins.put(curOrigin, i);}modify += arr[i] - v;}return ans;}解法三:每个数字都减V,然后算这个数组中累加和小于等于0的子数组哪个最长
// 想实现的解法3,时间复杂度O(N)public static int ways3(int[] arr, int v) {if (arr == null || arr.length == 0) {return 0;}for (int i = 0; i < arr.length; i++) {arr[i] -= v;}return maxLengthAwesome(arr, 0);}// 找到数组中累加和<=k的最长子数组public static int maxLengthAwesome(int[] arr, int k) {int N = arr.length;int[] sums = new int[N];int[] ends = new int[N];sums[N - 1] = arr[N - 1];ends[N - 1] = N - 1;for (int i = N - 2; i >= 0; i--) {if (sums[i + 1] < 0) {sums[i] = arr[i] + sums[i + 1];ends[i] = ends[i + 1];} else {sums[i] = arr[i];ends[i] = i;}}int end = 0;int sum = 0;int res = 0;for (int i = 0; i < N; i++) {while (end < N && sum + sums[end] <= k) {sum += sums[end];end = ends[end] + 1;}res = Math.max(res, end - i);if (end > i) {sum -= arr[i];} else {end = i + 1;}}return res;}总结
题目一主要技巧:利用单调性优化
题目二主要技巧:利用预处理结构优化 + 讨论开头结尾
题目三主要技巧:假设答案法+淘汰可能性(很难,以后还会见到)
题目五
给定一个正方形矩阵matrix,原地调整成顺时针90度转动的样子
a b c g d a
d e f h e b
g h i i f c
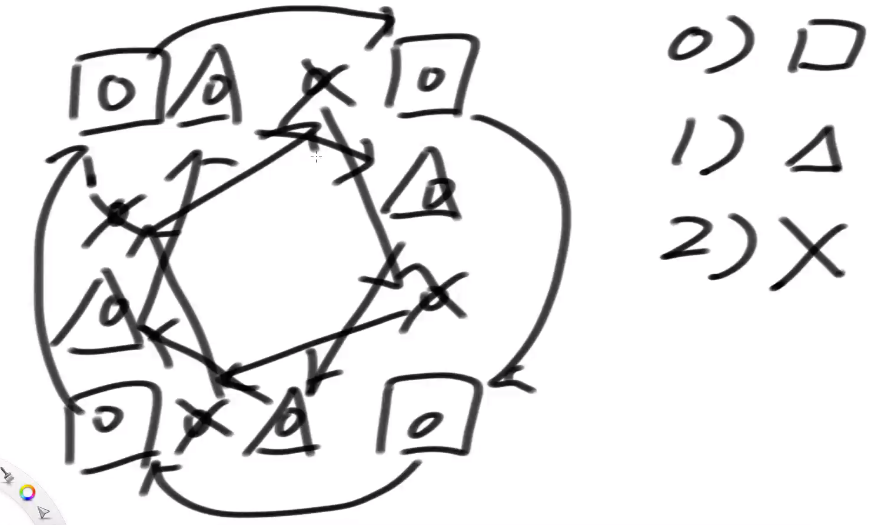
public static void spiralOrderPrint(int[][] matrix) {int tR = 0;int tC = 0;int dR = matrix.length - 1;int dC = matrix[0].length - 1;while (tR <= dR && tC <= dC) {printEdge(matrix, tR++, tC++, dR--, dC--);}}public static void printEdge(int[][] m, int tR, int tC, int dR, int dC) {if (tR == dR) {for (int i = tC; i <= dC; i++) {System.out.print(m[tR][i] + " ");}} else if (tC == dC) {for (int i = tR; i <= dR; i++) {System.out.print(m[i][tC] + " ");}} else {int curC = tC;int curR = tR;while (curC != dC) {System.out.print(m[tR][curC] + " ");curC++;}while (curR != dR) {System.out.print(m[curR][dC] + " ");curR++;}while (curC != tC) {System.out.print(m[dR][curC] + " ");curC--;}while (curR != tR) {System.out.print(m[curR][tC] + " ");curR--;}}}题目六
给定一个长方形矩阵matrix,实现转圈打印
a b c d
e f g h
i j k L
打印顺序:a b c d h L k j I e f g
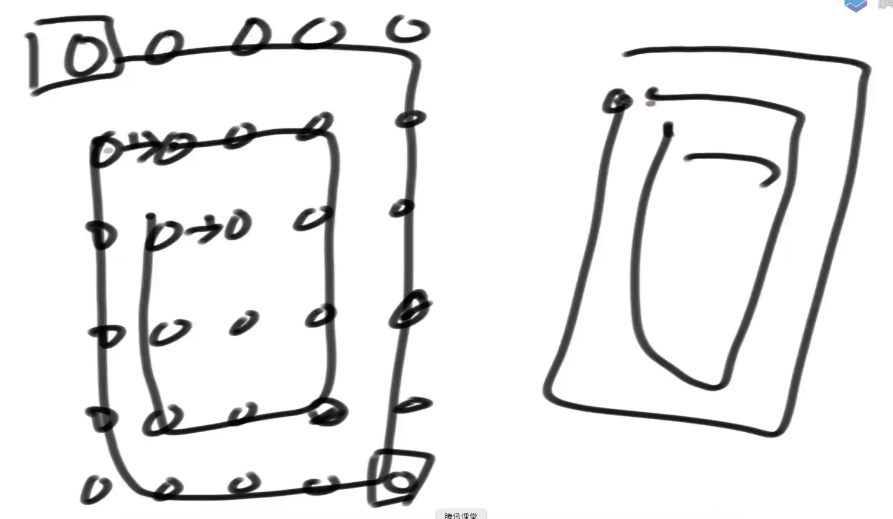
public static void rotate(int[][] matrix) {int a = 0;int b = 0;int c = matrix.length - 1;int d = matrix[0].length - 1;while (a < c) {rotateEdge(matrix, a++, b++, c--, d--);}}public static void rotateEdge(int[][] m, int a, int b, int c, int d) {int tmp = 0;for (int i = 0; i < d - b; i++) {tmp = m[a][b + i];m[a][b + i] = m[c - i][b];m[c - i][b] = m[c][d - i];m[c][d - i] = m[a + i][d];m[a + i][d] = tmp;}}题目七
给定一个正方形或者长方形矩阵matrix,实现zigzag打印
0 1 2
3 4 5
6 7 8
打印: 0 1 3 6 4 2 5 7 8
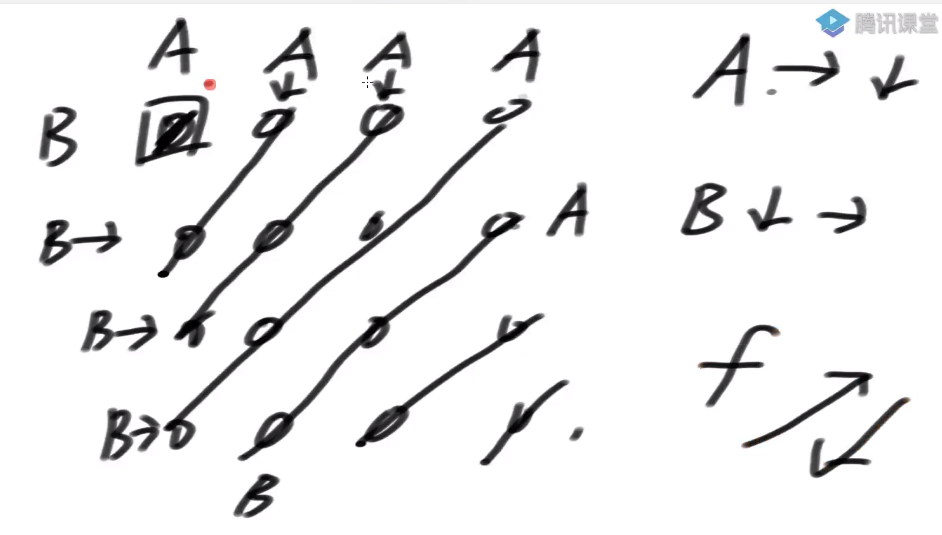
public static void printMatrixZigZag(int[][] matrix) {int tR = 0;int tC = 0;int dR = 0;int dC = 0;int endR = matrix.length - 1;int endC = matrix[0].length - 1;boolean fromUp = false;while (tR != endR + 1) {printLevel(matrix, tR, tC, dR, dC, fromUp);tR = tC == endC ? tR + 1 : tR;tC = tC == endC ? tC : tC + 1;dC = dR == endR ? dC + 1 : dC;dR = dR == endR ? dR : dR + 1;fromUp = !fromUp;}System.out.println();}public static void printLevel(int[][] m, int tR, int tC, int dR, int dC, boolean f) {if (f) {while (tR != dR + 1) {System.out.print(m[tR++][tC--] + " ");}} else {while (dR != tR - 1) {System.out.print(m[dR--][dC++] + " ");}}}
这篇关于算法数据结构(三十五)----子数组达到累加和的最大长度系列的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




