本文主要是介绍二分查找算法:穿越算法迷宫的指南,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
✨✨✨学习的道路很枯燥,希望我们能并肩走下来!
目录
前言
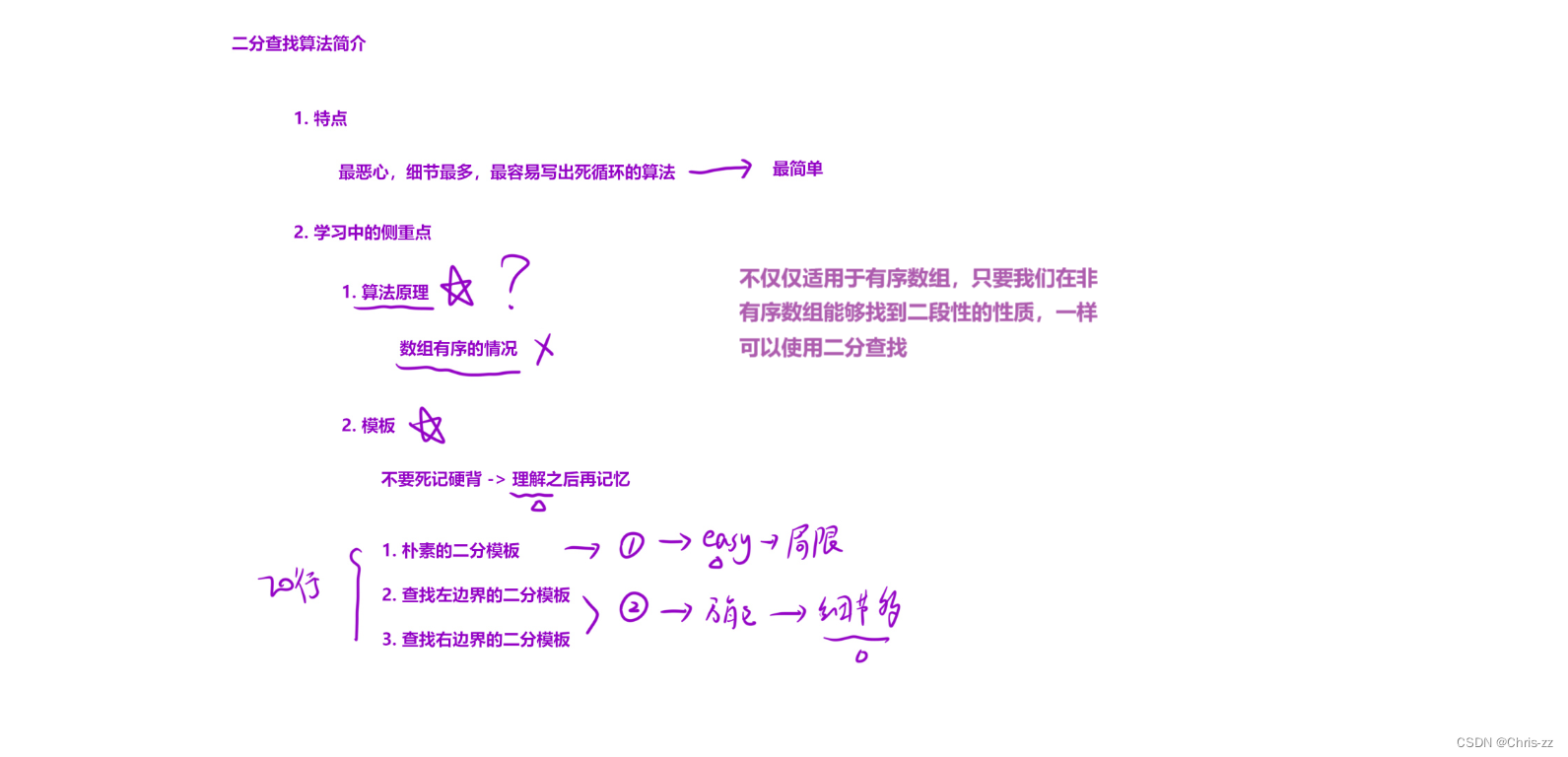
一. 二分查找算法介绍
二 二分查找的题目解析
2.1 二分查找
2.2 在排序数组中查找元素的第一个位置和最后一个位置
2.3 搜索插入位置
2.4 x的平方根
2.5 山峰数组峰顶的索引
2.6 寻找峰值
2.7 寻找旋转数组中的最小值
2.8 点名
三. 二分算法总结+模板
总结
前言
本篇详细介绍了二分查找算法的使用,让使用者了解二分查找,而不是仅仅停留在表面, 文章可能出现错误,如有请在评论区指正,让我们一起交流,共同进步!
一. 二分查找算法介绍
二. 二分查找的题目解析
开始之前可以去总结部分被去看看模板,再结合题目理解
2.1 二分查找
704. 二分查找 - 力扣(LeetCode)

思路:(模版1)正常的二分查找策略
class Solution {
public:int search(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;while (left <= right) {int mid = (right - left) / 2 + left;if (nums[mid] == target) return mid;else if (nums[mid] > target) right = mid - 1;else left = mid + 1;}return -1;}
};2.2 在排序数组中查找元素的第一个位置和最后一个位置
34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣(LeetCode)
 思路:找第一个,用左区间端点查找(模版2),找最后一个,用右端点区间查找(模版3)
思路:找第一个,用左区间端点查找(模版2),找最后一个,用右端点区间查找(模版3) 
class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {//处理边界情况if(nums.size() == 0) return {-1,-1};int left = 0;int right = nums.size()-1;int first = 0;// 1.二分左端点while(left<right) //先找第一次的{int mid = (right - left)/2+left;if(nums[mid] >= target){right = mid;}else{left = mid +1;}}//判断是否有结果if(nums[left] != target) return {-1,-1};else first = left; //标记一下左端点// 2.二分右端点left = 0,right = nums.size()-1;while(left<right){int mid = (right - left+1)/2+left;if(nums[mid] <= target){left = mid;}else{right = mid -1;}}return {first,right};}
};2.3 搜索插入位置
35. 搜索插入位置 - 力扣(LeetCode)
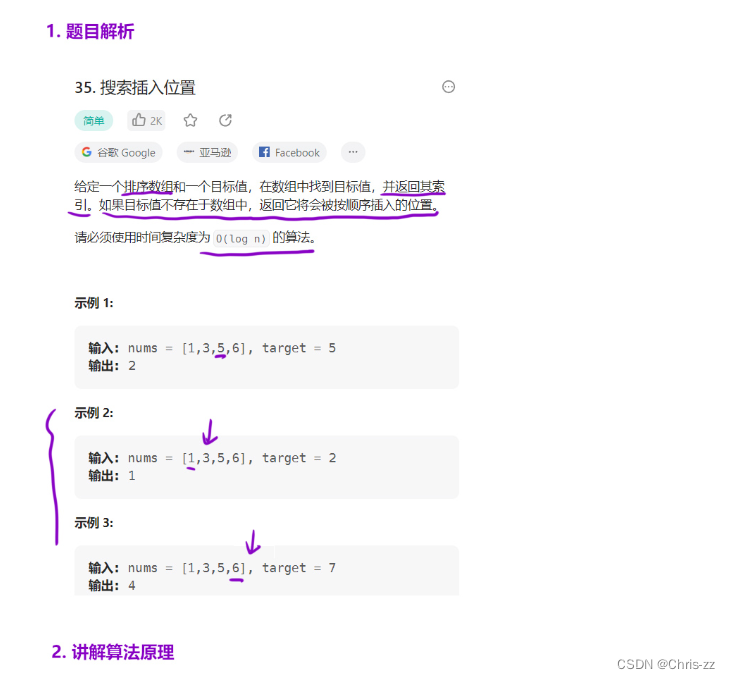 思路:左端区间查找 (右区间查找也行
思路:左端区间查找 (右区间查找也行
class Solution {
public:int searchInsert(vector<int>& nums, int target) {int left = 0, right = nums.size()-1;if(nums[right]<target) return right + 1;while(left < right){int mid = (right - left)/2 + left;if(nums[mid]>=target) right = mid;else left = mid + 1;}return left;}
};2.4 x的平方根
69. x 的平方根 - 力扣(LeetCode)
 思路:右端区间二分查找法
思路:右端区间二分查找法 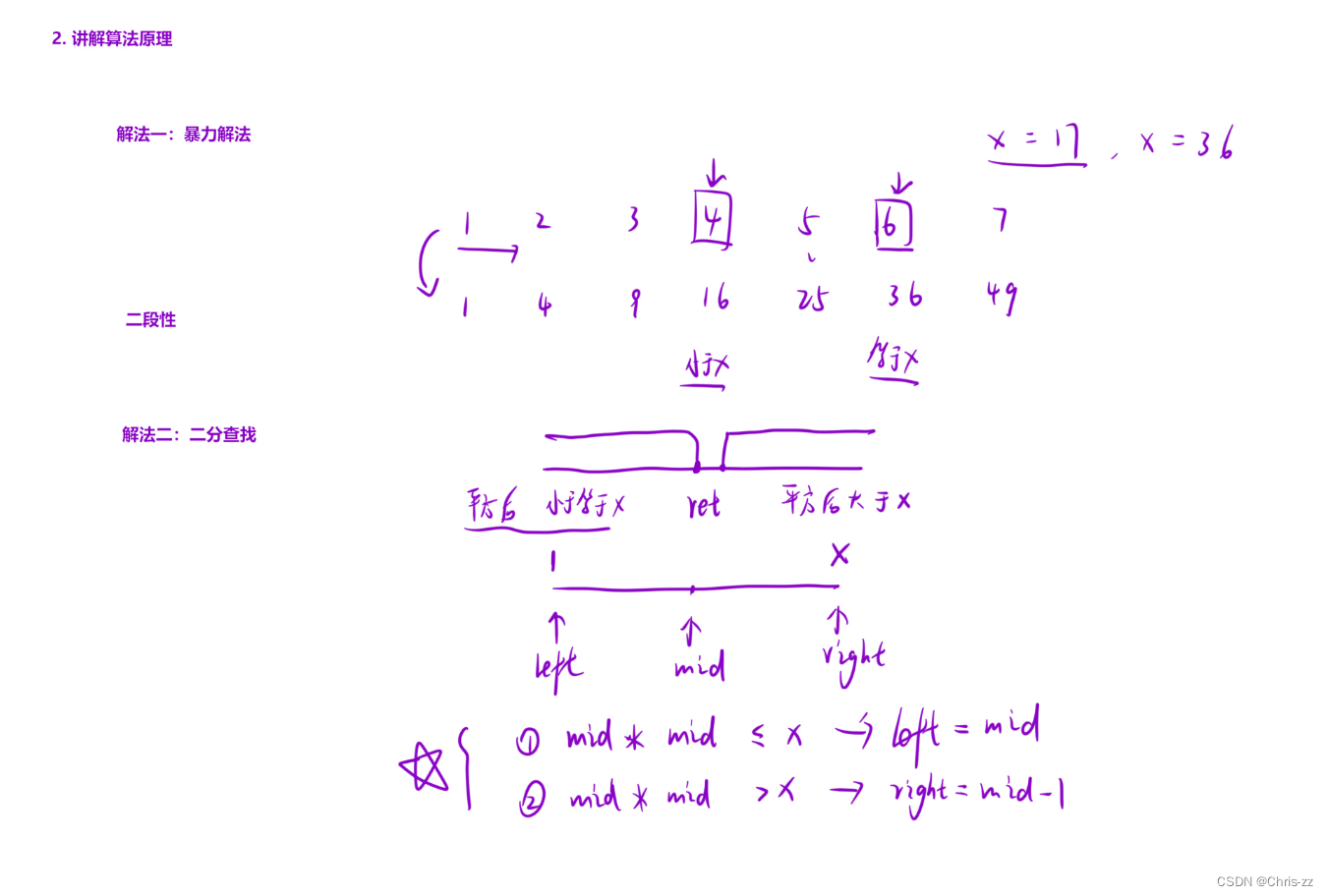
class Solution {
public:int mySqrt(int x) {if(x == 0) return 0; //处理边界情况int left = 1, right = x;while(left<right){long long mid = (right - left + 1) /2+left; //防溢出if(mid*mid<=x) left = mid;else right = mid - 1;}return left;}
};2.5 山峰数组峰顶的索引
852. 山脉数组的峰顶索引 - 力扣(LeetCode)
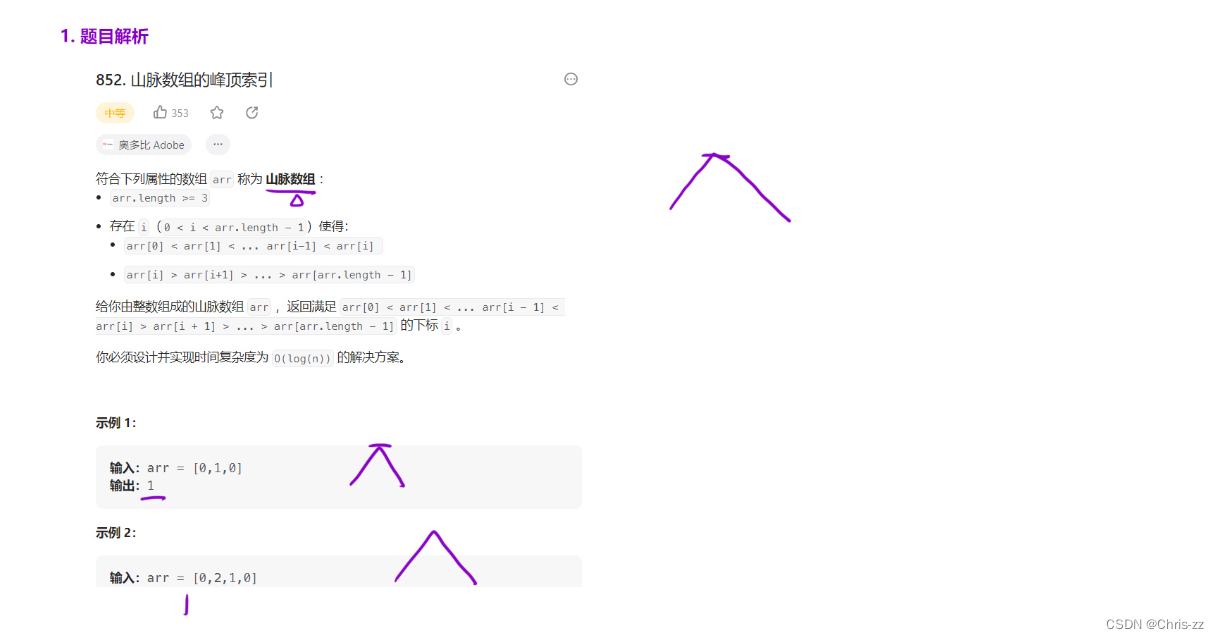
思路:左或右端区间查找

class Solution {
public:int peakIndexInMountainArray(vector<int>& arr) {int left = 1 ,right = arr.size()- 2;while(left < right){int mid = (right - left + 1) / 2 + left;if(arr[mid]>arr[mid-1]) left = mid;else right = mid - 1;}return left;}
};2.6 寻找峰值
162. 寻找峰值 - 力扣(LeetCode)
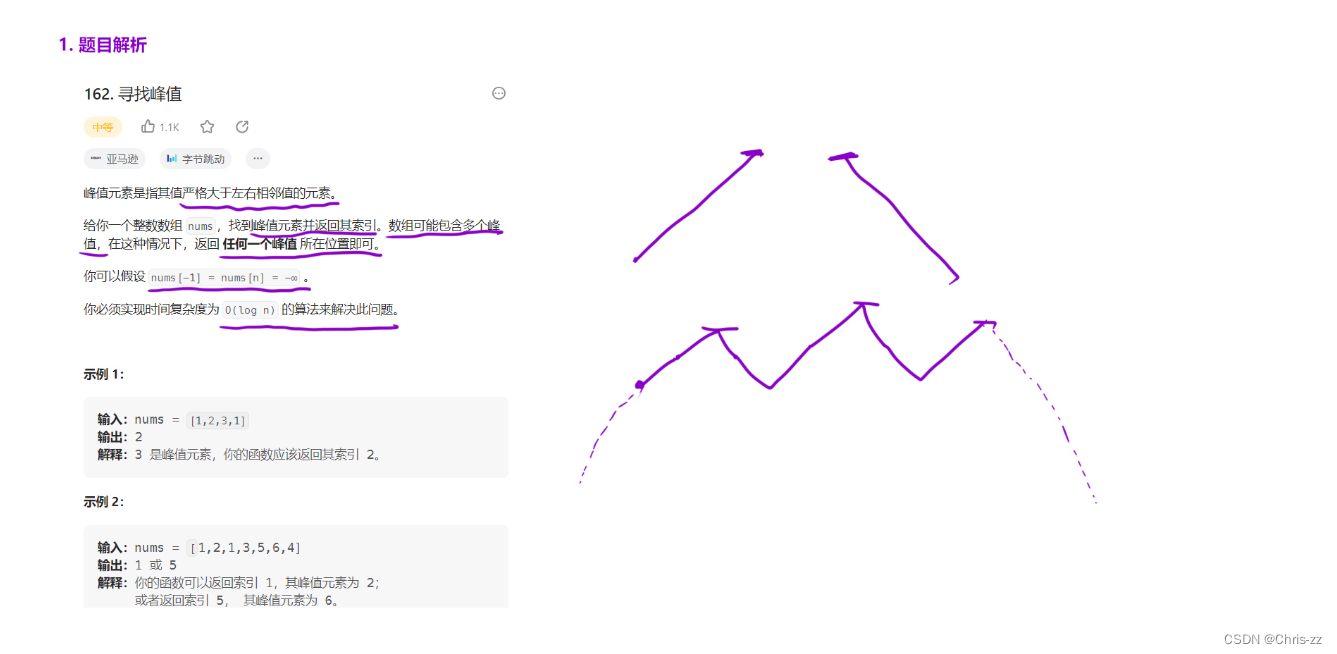 思路:左或右端点区间查找
思路:左或右端点区间查找
 右区间:
右区间:
class Solution {
public:int findPeakElement(vector<int>& nums) {int left = 0, right = nums.size()-1;while(left < right){int mid = (right - left) / 2 + left;if(nums[mid]<nums[mid+1]) left = mid + 1;else right = mid;}return left;}
};2.7 寻找旋转数组中的最小值
153. 寻找旋转排序数组中的最小值 - 力扣(LeetCode)

思路:左区间端点查找法

class Solution {
public:int findMin(vector<int>& nums) {int left = 0, right = nums.size()-1;int n = nums.size();while(left<right){int mid = (right - left)/2+left;if(nums[mid]>nums[n-1]) left = mid + 1;else right = mid;}return nums[left];}
};2.8 点名
LCR 173. 点名 - 力扣(LeetCode)
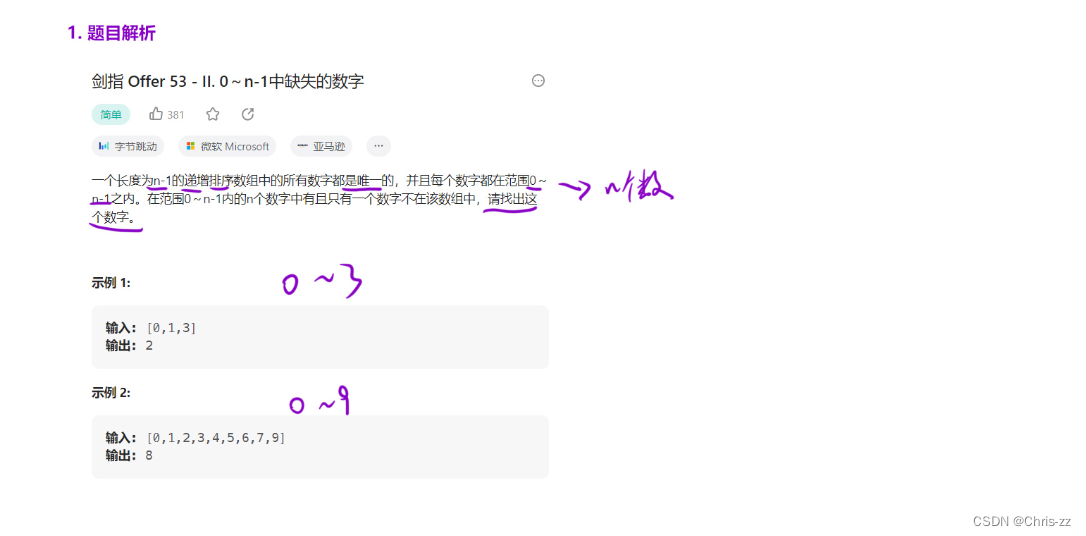
 思路:左区间查找
思路:左区间查找
class Solution {
public:int takeAttendance(vector<int>& records) {int left = 0, right = records.size()-1;while(left<right){int mid = (right - left)/2+left;if(records[mid] == mid) left = mid + 1;else right = mid;}//处理细节问题:最后一个位置缺少return records[left] == left ? left+1 : left;}
};三. 二分算法总结+模板
二分查找的策略基本上都是去找一个数,对应的有三种模版:正常的二分查找、左区间端点查找、右区间端点查找。其中正常的二分查找局限性比较大,必须得是升序且限制条件较多,大多数情况下不符合题意。最常用的就是左区间端点(关键是left会大跳跃,且目标位置在较大值区间的左边)和右区间端点法(关键是right会大跳跃,且目标位置在较小值区间的右边)。
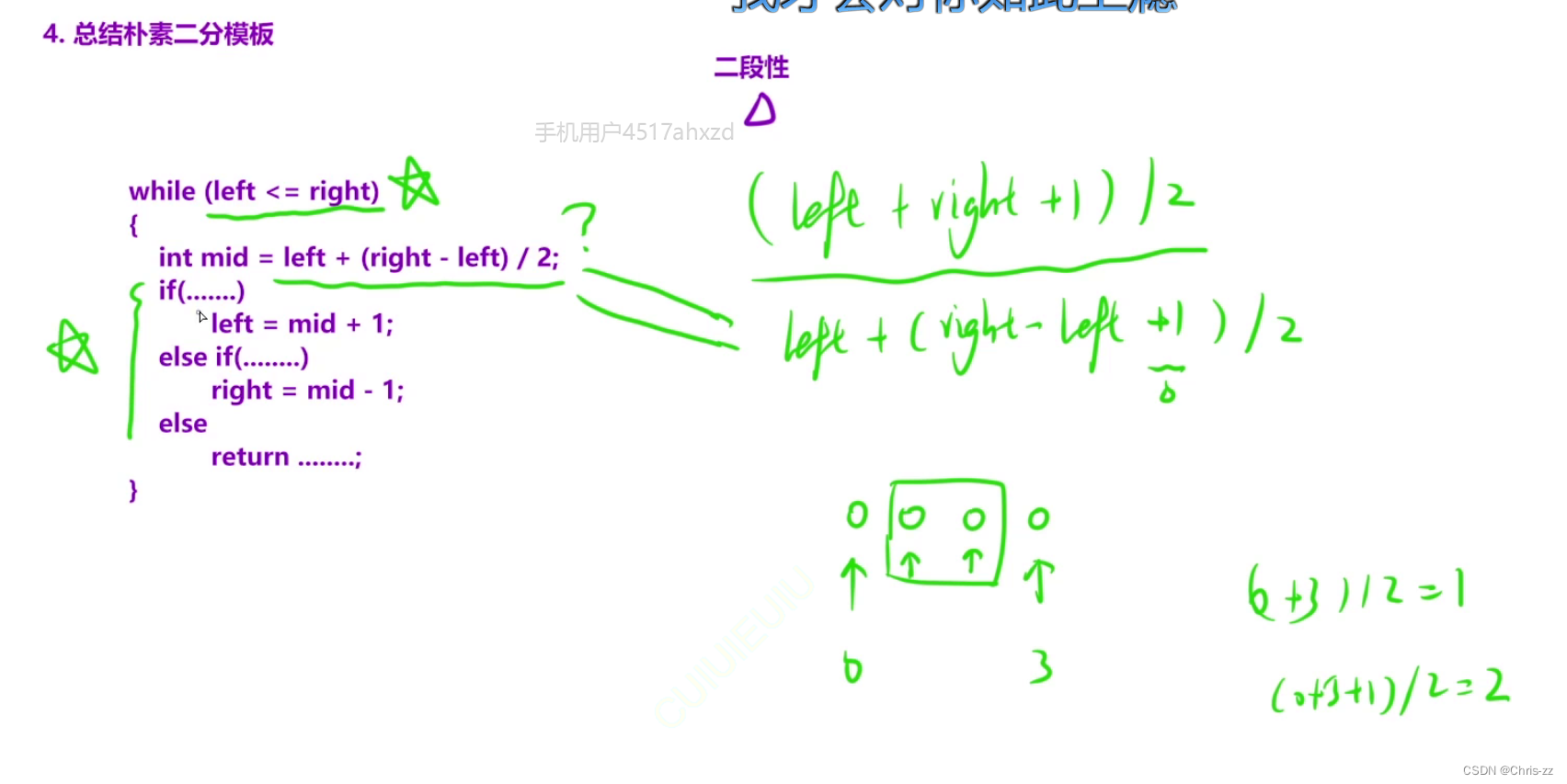

图from:算法思想总结:二分查找算法-CSDN博客
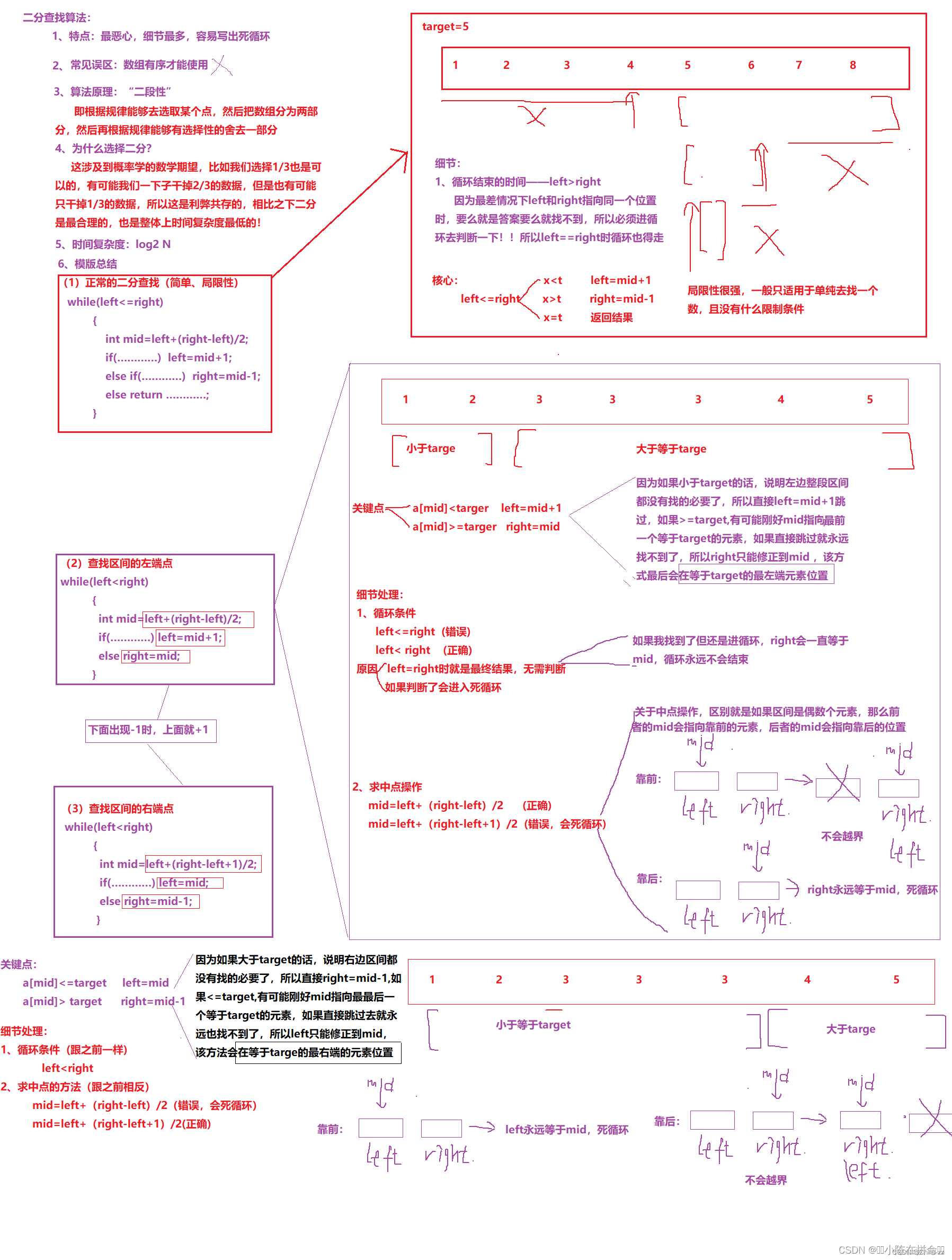
总结
✨✨✨各位读友,本篇分享到内容是否更好的让你理解二分查找算法,如果对你有帮助给个👍赞鼓励一下吧!!
🎉🎉🎉世上没有绝望的处境,只有对处境绝望的人。
感谢每一位一起走到这的伙伴,我们可以一起交流进步!!!一起加油吧!!
这篇关于二分查找算法:穿越算法迷宫的指南的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






