本文主要是介绍工业镜头孔径、分辨率与景深参数简析,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
工业镜头孔径、分辨率与景深参数简析
- 一、前言
- 二、镜头孔径与光圈系数
- 2.1孔径与相对孔径
- 2.2数值孔径(NA)
- 2.3光圈系数(F/#)
- 2.4工作光圈系数((F/#)w)
- 三、镜头分辨率
- 3.1MTF与CTF
- 3.1.1MTF(调制传递函数,Modulation Transfer Function)
- 3.1.2CTF(对比度传递函数,Contrast Transfer Function)
- 3.2空间频率与像侧分辨率
- 3.2.1空间频率与像侧分辨率的定义
- 3.2.2空间频率、像侧分辨率与MTF曲线的关系
- 3.3理想镜头分辨率
- 四、景深(DOF,depth of field)
- 4.1景深定义
- 4.2景深的计算公式
- 4.2.1景深的理论计算公式
- 4.2.2远心镜头景深的经验计算公式
- 参考文档
一、前言
本文承接本博客的另一篇文章工业相机和镜头参数简析,对文中的几个镜头参数进一步说明,并补充记录其他参数。读者可先阅读工业相机和镜头参数简析,也可直接阅读本文。
二、镜头孔径与光圈系数
2.1孔径与相对孔径
一般的镜头都是由多片镜片组合而成,光线经过这些镜片到达成像面时,并不是所有的光线都能通过,而是有一部分被阻挡了,就好像光线通过一个孔,孔越大,通过的光线越多,在像平面上所成的像越亮,这个圆孔也被称为孔径光阑、入射光瞳、出射光瞳,圆孔的直径称为孔径或有效孔径。
相对孔径为孔径与焦距的比值:D/f,镜头像面的照度与相对孔径的平方成正比。
2.2数值孔径(NA)
数值孔径(Numerical Aperture, NA),定义为光学系统中镜头光轴和边缘光线之间的角度半角的正弦值与系统的折射率的乘积。计算公式为:NA=n⋅sin(θ)。
n 是介质的折射率(例如空气的折射率通常为 1,水的折射率约为 1.33);
θ 是镜头光轴和最大接受光线之间的半角,称为接受角(acceptance angle),如下图所示:
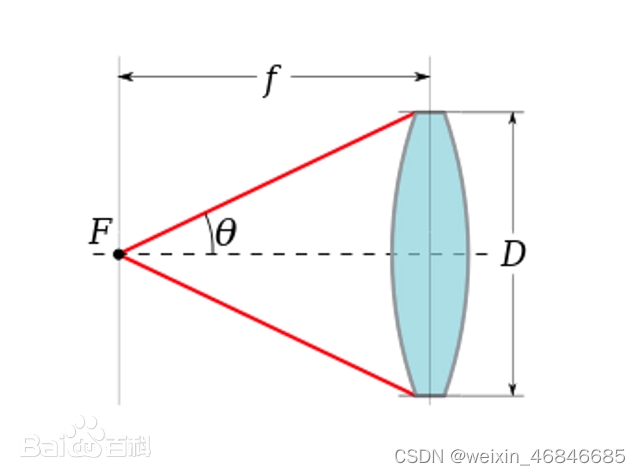
图中D即是孔径。
当θ较小时,有近似关系:tan(θ)≈sin(θ),而tan(θ)=D/2f,所以有NA的近似公式:NA≈n⋅D/2f。
2.3光圈系数(F/#)
光圈系数是镜头相对孔径的倒数,即焦距与孔径的比值:f/D。光圈系数的标称值数字越大,也就表示其实际光圈就越小。一般的厂家都会用 F 数来表示这一参数。

镜头的光圈排列顺序是: 1、 1.4、 2.0、 2.8、 3.5、 4.0、 5.6、 8.0、 11、 16、 22、 32 等等, F/#的大小是通常通过改变光圈调整环的大小来设置的。随着数值的增大,其实际光孔大小也就随之减小,而其在相同快门时间内的光通量也就随之减小。
根据光圈系数的定义,可得出NA与F/#的关系为:NA≈n⋅/2F/#,而空气的折射率n=1,所以有:NA≈1⋅/2F/#。
2.4工作光圈系数((F/#)w)
标准光圈系数(F/#) 是在无放大或缩小的理想条件下定义的,实际上,当存在放大倍率M时,图像侧的光束收集能力不仅仅取决于焦距和有效孔径,还需要考虑到放大倍率对光束的影响。
工作光圈系数也称工作 f-数,是指在实际成像条件下,光学系统的光线收集能力,计算公式如下:
(F/#)w=(1+M)⋅F/#
M为放大倍率,注意放大倍率为成像尺寸除以物体尺寸。
三、镜头分辨率
镜头的分辨率表征在成像过程中镜头区分细节能力的大小,在镜头的参数文件中有时会给出MTF曲线、CTF值描述分辨率大小,有时会给出以lp/mm为单位的空间频率值或以μm为单位的像侧分辨率描述分辨率大小。
3.1MTF与CTF
3.1.1MTF(调制传递函数,Modulation Transfer Function)
MTF 描述了镜头在不同空间频率下的对比度传递能力,衡量成像再现物体的表面的浓淡变化即对比度的程度。它是镜头分辨率的重要指标,反映了镜头在解析图像细节时的能力,是很客观很准确的一种镜头评价方法。
测量MTF用的是具有特定空间周波数的黑白间隔测试, 空间周波数是指 1mm 的距离浓淡变化的程度。
MTF通常是以曲线图的形式出现在镜头参数文件中,例如描述MTF随空间频率的变化的曲线,空间频率(spatial frequency)的单位是 lp/mm,即 1 毫米距离内的黑白线对数,MTF的值从100%逐渐下降趋于0,如下图:
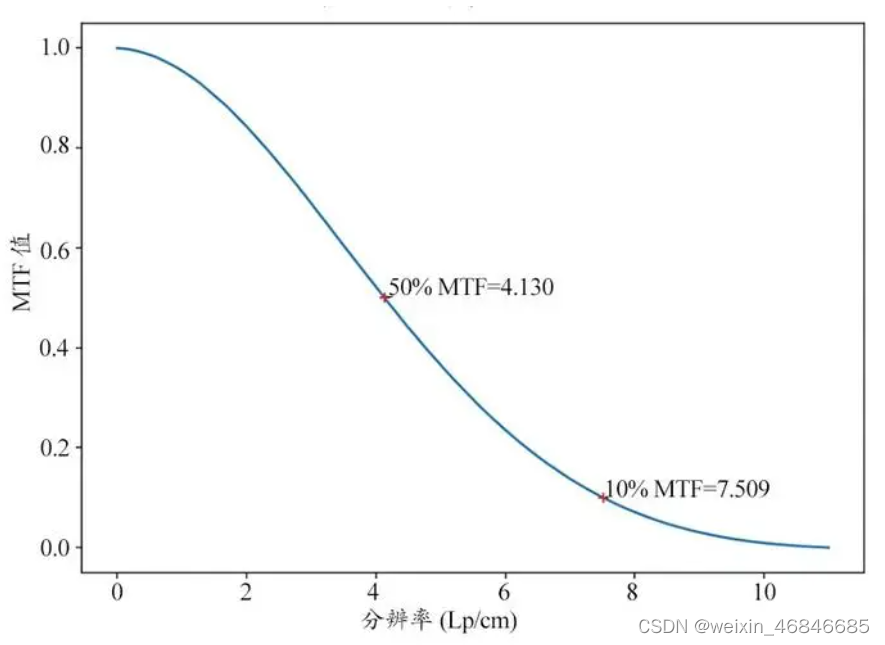
还有描述在不同位置处成像MTF变化的曲线,主要分为三种:
- 沿径向的MTF曲线
径向是指沿直径方向,即从镜头中心到边缘(不同半径位置)的MTF如何变化。通常,径向MTF在不同的距中心距离(如0mm、5mm、10mm等)进行测量,生成一组MTF曲线,称为弧矢曲线, 标为 S(Sagittal),通常MTF会随距中心的距离增加而下降,这表明边缘区域的解析能力较低。 - 沿轴向的MTF曲线
轴向是指沿光轴方向,即镜头在不同焦距或景深位置的MTF变化。轴向MTF在不同焦距或不同焦平面上进行测量,生成一组MTF曲线,称为子午曲线, 标为 M(Meridional)。 - 随视场角变化的MTF曲线
不同的视场角对应于图像的从中心到边缘的不同区域,,视场角MTF是在这些不同区域进行测量。通常,随着视场角的增大,MTF值会下降,在中心处(0°视场角)通常具有最高的MTF值。
轴向MTF测量,保持视场角固定,通常选择0°视场角,即镜头中心处,来测量离焦平面不同轴向距离处的MTF。
径向MTF测量通常是在固定的焦平面上进行的,轴向距离保持不变,所以它的变化曲线与随视场角变化的MTF曲线走向是一样的。
不同位置MTF曲线图如下图:
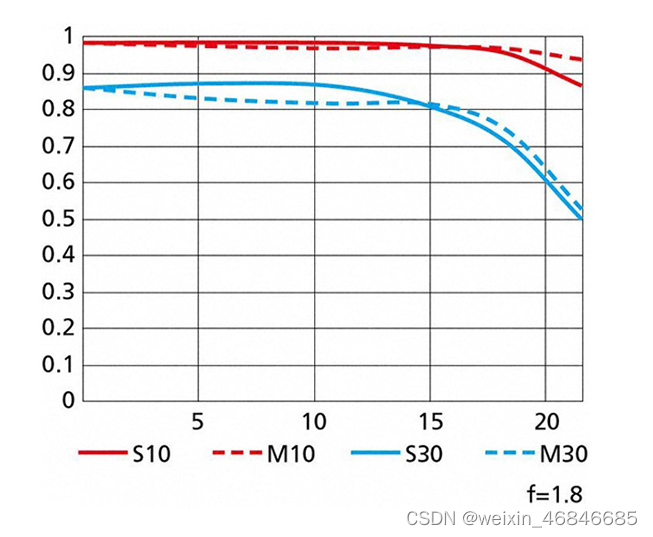
3.1.2CTF(对比度传递函数,Contrast Transfer Function)
CTF是MTF的一个特定点,是指某个特定的空间频率下(如70lp/mm)测量的对比度传递能力。
同一频率下MTF值不同导致的成像差异如下图:


3.2空间频率与像侧分辨率
3.2.1空间频率与像侧分辨率的定义
- 空间频率
单位为线对每毫米(lp/mm),表示镜头能够在1mm 间距内能分辨开的黑白相间的线条对数。例如,100 lp/mm的分辨率表示镜头可以区分1 mm内有100对黑白线条。每个线条默认是1个像素宽,那么相当于镜头中的每个像素尺寸为1000÷(100×2)=5μm。 - 像侧分辨率
以微米(µm)为单位,表示镜头在成像平面上能够解析的最小特征尺寸,大多数情况下是指系统能够分辨的最小线对间隔。例如,镜头像侧分辨率为10µm,则单个像素尺寸为5µm。
这两种单位可相互转换,例如125lp/mm的镜头,那么1mm能够解析出125个线对,像侧分辨率即为8μm。
当使用像侧分辨率描述镜头的分辨率时,此时镜头分辨率应≤2*相机的像素尺寸,例如相机像素尺寸为5μm,那么可以选择10μm及以下分辨率的镜头。
使用lp/mm为单位描述镜头的分辨率时,如何匹配选型可见工业相机和镜头参数简析。
3.2.2空间频率、像侧分辨率与MTF曲线的关系
如果使用空间频率值或像侧分辨率描述分辨率大小,那么该值通常是镜头的极限分辨率或者是对应于MTF曲线的特定点。
例如MTF = 0.5 (50%)的空间频率值或像侧分辨率,表示在该分辨率下,镜头传递的对比度为50%。这个值通常被认为是镜头的实际有效分辨率,因为它保持了较高的图像质量。
镜头的极限分辨率,也称为镜头的截止频率,这是镜头能够分辨的最高空间频率,在此空间频率下MTF接近零。
当在某个高空间频率下MTF非常低时,虽然表示对比度很低,但在某些高分辨率和特定应用中仍然有价值,尤其是经过后处理的增强。能否在MTF为10%的条件下正常使用镜头,取决于具体的应用需求。如果应用场景需要识别或检测极高频率的细节,那么10% MTF仍然可以提供有用的信息。
3.3理想镜头分辨率
在光学中,理想镜头的分辨率(也称为衍射极限分辨率)是由镜头的光圈和入射波长决定的,它表示镜头在最佳情况下能分辨的最小细节。
光波通过光圈后会发生衍射,衍射效应限制了镜头的分辨能力。根据瑞利判据,两个点能被分辨的条件是它们的衍射图样的第一暗环与另一点的中心衍射峰重合。
镜头的理想分辨率计算公式如下:
理想分辨率=0.61λ/(n⋅sinθ),λ为入射光波长,在粗略计算中可近似为0.55μm。
根据上文所述数值孔径及光圈系数的定义有:
理想分辨率=0.61λ/(n⋅sinθ)=0.61λ/NA≈0.61λ/(n⋅D/2f)=1.22λ⋅F/#/n,F/#为光圈系数,又因为空气的折射率n=1而有如下公式:
理想分辨率=1.22λ⋅F/#。
考虑到实际使用中的光学系统放大倍率的影响,计算公式应使用工作光圈系数(F/#)w,因此最终计算公式为:
理想分辨率=1.22λ⋅(F/#)w=1.22λ⋅F/#⋅(1+M)。
由理想镜头分辨率的计算公式可知,调大光圈即光圈系数减小,会提高分辨率,反之会降低分辨率。
四、景深(DOF,depth of field)
4.1景深定义
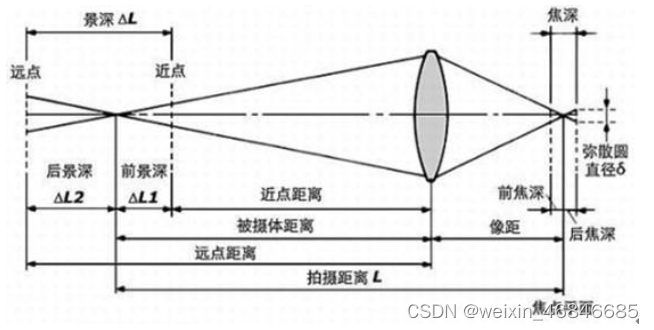
镜头对着某个物体聚焦清晰时,可以在传感器上相当清晰的成像,在这个平面沿着镜头轴线的前面和后面一定范围的点也可以结成较清晰的像点,这前后两个平面之间的距离叫景深。
景深表示在垂直镜头光轴轴线的同一平面内的点,满足图像清晰度要求的最远位置与最近位置的差值。
景深分为:
- 前景深(Near DOF):物平面前能够保持清晰的最近距离。
- 后景深(Far DOF):物平面后能够保持清晰的最远距离。
- 总景深(Total DOF):前景深和后景深之和,表示整个平面前后清晰的区域。
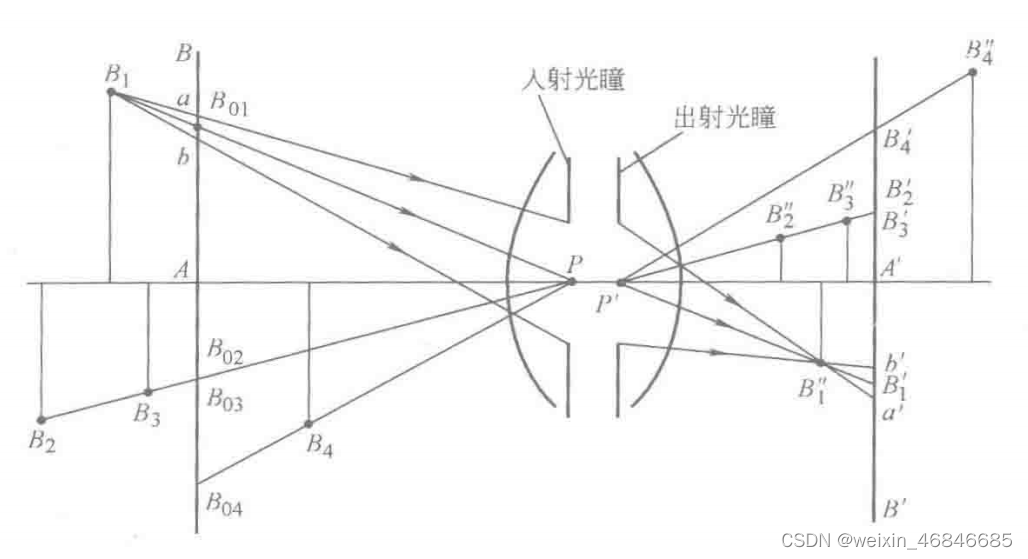
4.2景深的计算公式
4.2.1景深的理论计算公式
前景深ΔL1=FδL²/(f²+FδL)
后景深ΔL2=FδL²/(f²-FδL)
景深ΔL=ΔL1+ΔL2=(2f²FδL²) /(f⁴-F²δ²L²)
另一景深计算公式为ΔL=2 × (F/#)w × δ ÷ M²
其中:
δ——容许弥散圆直径,可使用相机的像素尺寸;
f ——镜头焦距;
F——镜头的光圈系数;
L——对焦距离,可使工作距离与焦距相加得到;
(F/#)w——工作光圈系数;
M——放大倍率,注意放大倍率为成像尺寸除以物体尺寸。
从景深计算公式可知:
- 后景深大于前景深;
- 调大光圈,光圈系数减小,则景深减小,反之会增大景深。
4.2.2远心镜头景深的经验计算公式
参照Opto Engineering公司官网Opto Engineering——Frequently asked questions,景深是一个复杂的参数,难以通过理论计算得出,因此官网给出了经验计算公式如下:
DOF = (WFN * p * k) / (M * M)
其中:
M——放大倍率,注意放大倍率为成像尺寸除以物体尺寸;
WFN——工作光圈系数;
p——像素尺寸,单位为μm而不是mm;
k——特定参数,大小取决于应用场景,镜头用于测量时应取0.008,用于检测缺陷时应取0.015。
参考文档
景深计算公式的推导
Opto Engineering——Frequently asked questions
这篇关于工业镜头孔径、分辨率与景深参数简析的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



