NYOJ 91题阶乘之和（贪心算法）

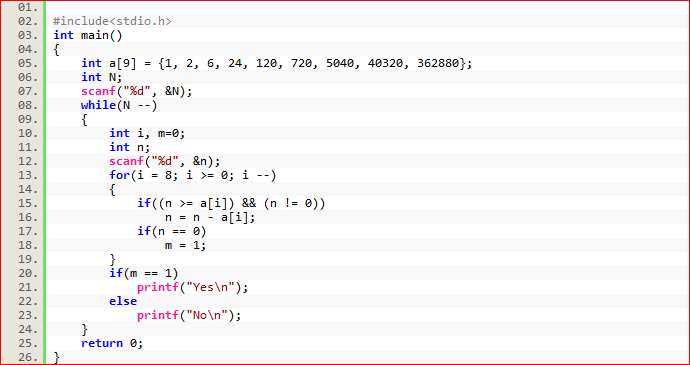
本文主要是介绍NYOJ 91题阶乘之和（贪心算法），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

开始时，先算出了，从1到10的阶乘{1, 2, 6, 24, 120, 720, 5040, 40320, 362880，,328800}，心想，就是这前9中里面的任意组合，于是，想要标记出所有可以用阶乘表示的数。无奈，后来发现，个数太多，根本就无法表示出来。于是上网搜资料，才知道，这是用了贪心算法。

下面是复制的关于贪心算法的介绍：

贪心算法（又叫贪婪算法），是指在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上考虑，他所做出的仅是在某种意义上的局部最优解。贪心算法,不是对所有问题都能得到整体最优解，但对范围相当广泛的许多问题，它能产生整体最优解或者整体最优解的近似解。

贪婪算法可解决的问题通常大部分都有如下的特性：

⑴ 有一个以最优方式来解决的问题。为了构造问题的解决方案，有一个候选的对象的集合：比如不同面值的硬币。

⑵ 随着算法的进行，将积累起其它两个集合：一个包含已经被考虑过并被选出的候选对象，另一个包含已经被考虑过但被丢弃的候选对象。

⑶ 有一个函数来检查一个候选对象的集合是否提供了问题的解答。该函数不考虑此时的解决方法是否最优。

⑷ 还有一个函数检查是否一个候选对象的集合是可行的，也即是否可能往该集合上添加更多的候选对象以获得一个解。和上一个函数一样，此时不考虑解决方法的最优性。

⑸ 选择函数可以指出哪一个剩余的候选对象最有希望构成问题的解。

⑹ 最后，目标函数给出解的值。

为了解决问题，需要寻找一个构成解的候选对象集合，它可以优化目标函数，贪婪算法一步一步的进行。起初，算法选出的候选对象的集合为空。接下来的每一步中，根据选择函数，算法从剩余候选对象中选出最有希望构成解的对象。如果集合中加上该对象后不可行，那么该对象就被丢弃并不再考虑；否则就加到集合里。每一次都扩充集合，并检查该集合是否构成解。如果贪婪算法正确工作，那么找到的第一个解通常是最优的。

于是这道题的思路：

1.先求最接近n的阶乘；

2.每次找到最接近n的阶乘之后，n = n - a[i]，之后，重复查找最接近n的阶乘数（关键步骤）；

3.若 n == 0,则n可以分解成阶乘之和，反之不能。