本文主要是介绍2016 Multi-University Training Contest 2-1005---HDU 5738 Eureka,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题目链接:HDU 5738
题意:
xjb推导一下可以知道best set一定是一些共线的点, 于是问题变成问有多少个点集共线.
题解:
最基本的想法是,两点确定一条直线,然后判断其他点是否在这条直线上,但是O(N^3)复杂度太高。
可以以一点为基本点,判断其他点与这个点的斜率,将斜率与其对应的点数用map存下来,斜率相等表示都与这个点共线共线。所有点都判断完成后计算与这个点共线的点集数。
计算当前点共线的子集数:从某个点出发,假设与其共线的其他点共有n个,则可以将该点可以与其他点组成的任意一个非空子集(共有2^n-1)组成一个点集。
注意:
1.斜率正负的转化。
2.斜率为0和斜率不存在的情况。
3.重点的情况。我们用重点集来表示一个点相同的点的集合。
举例来说明:有(0,0),(0,0),(0,0),(0,1),(0,2),(1,0),(2,0)七个点,以第一个点为基本点判断时,第4,5两个点(0,1)(0,2)与第一个点(0,0)构成斜率为[0,1](斜率不存在都用[0,1]表示)的组合两种,第6,7两个点(1,0)(2,0)与第一个点(0,0)构成斜率为[1,0](斜率为0都用[1,0]表示)的组合两种,以上每种组合都可以与第一个点的重点集(第二个和第三个(0,0))的任意一个子集(可以为空,空的时候为原点集,共有2^n)构成一种结果点集,同时第一个点本身也可以与其重点集的非空子集(共有2^n-1个)构成一种结果集。
所以如果非重点的组合共有now种,重点共有cnt个,则总共的结果点集数为:
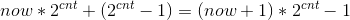
代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<map>
#include<cmath>using namespace std;
const int MAX = 1000 + 10;
const int MOD = 1e9+7;
typedef long long LL;
typedef pair<int,int> point;
typedef point slope;point p[MAX];
map<slope, int> num;
map<slope, int>::iterator it;int pow2[MAX];
void init()
{pow2[0]=1;for(int i=1;i<=1000;i++){pow2[i]=(pow2[i-1]*2)%MOD;}
}int main()
{//freopen("in.txt","r",stdin);//freopen("out.txt","w",stdout);int T;init();scanf("%d", &T);while(T--){int n;scanf("%d", &n);for(int i = 0; i < n; i++){scanf("%d%d", &p[i].first, &p[i].second);}LL ans = 0;for(int i = 0; i < n; i++){int cnt=0;for(int j = i + 1; j < n; j++){int dy = p[j].second - p[i].second;int dx = p[j].first - p[i].first;int sign=1;if((dx>0&&dy<0)||(dx<0&&dy>0))sign=-1;dx=abs(dx);dy=abs(dy);if(dx==0&&dy==0){cnt++;}else if(dx==0){num[slope(0,1)]++;}else if(dy==0){num[slope(1,0)]++;}else {int gxy=__gcd(dx,dy);dx=dx/gxy*sign;dy=dy/gxy;num[slope(dx,dy)]++;}}LL now=0;for(it = num.begin(); it != num.end(); it++){now=(now+pow2[it->second]-1)%MOD;}//now*(2^cnt)+(2^cnt-1)=(now+1)*(2^cnt)-1ans=(ans+(now+1)*pow2[cnt]-1)%MOD;num.clear();}printf("%d\n", (int)ans);}return 0;
}
官方题解给的是:
首先, 把所有点按照(x,y)双关键字排序, 然后枚举最左边的点i, 那么其他点j一定满足j > i. 把在这个点右边的点都做下排序(按照(dx, dy)/gcd(dx, dy)排序),这样排序并不是极角排序只是这样能够使得共线的 点相邻。 统计下共线的就好了. 需要注意下对重点的处理.其实核心和上面的思想是一样的,只不过排完序之后共线的点是挨着的,耗时可能会比较少。具体看代码,确实比不排序快了几百MS。
代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<map>
#include<cmath>using namespace std;
const int MAX = 1000 + 10;
const int MOD = 1e9+7;
typedef long long LL;
struct point
{int x,y;point(int x=0,int y=0):x(x),y(y){};bool operator <(const point &a) const{return this->x<a.x||(this->x==a.x&&this->y<a.y);}bool operator ==(const point &a) const{return this->x==a.x&&this->y==a.y;}void getslope(){int gxy=__gcd(x,y);x/=gxy;y/=gxy;}
};
typedef point slope;point p[MAX];
slope s[MAX];int pow2[MAX];
void init()
{pow2[0]=1;for(int i=1;i<=1000;i++){pow2[i]=(pow2[i-1]*2)%MOD;}
}int main()
{//freopen("in.txt","r",stdin);//freopen("out.txt","w",stdout);int T;init();scanf("%d", &T);while(T--){int n;scanf("%d", &n);for(int i = 0; i < n; i++){scanf("%d%d", &p[i].x, &p[i].y);}sort(p,p+n);LL ans = 0;for(int i = 0; i < n; i++){int cnt=0,m=0;for(int j = i + 1; j < n; j++){int dy = p[j].y - p[i].y;int dx = p[j].x - p[i].x;if(dx==0&&dy==0) cnt++;else {s[m]=slope(dx,dy);s[m++].getslope();}}sort(s,s+m);ans=(ans+pow2[cnt]-1)%MOD;for(int i=0,j;i<m;i=j){for(j=i+1;j<m&&s[i]==s[j];j++); ans=(ans+1ll*(pow2[j-i]-1)*pow2[cnt])%MOD;}}printf("%d\n", (int)ans);}return 0;
}这篇关于2016 Multi-University Training Contest 2-1005---HDU 5738 Eureka的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



