【算法专题--链表】环形链表--高频面试题（图文详解，小白一看就会！！）

本文主要是介绍【算法专题--链表】环形链表--高频面试题（图文详解，小白一看就会！！），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、前言

二、什么是环形链表？

🥝 环形链表的概念详解

🍇 环形链表的特点

🍍环形链表的延申问题

三、高频面试题

✨环形链表

✨环形链表II

✨环形链表的环长

四、总结

五、共勉

一、前言

环形链表，可以说是--链表专题--，最经典的一种结构，也是在面试中频率最高的一道题目，通常在面试中，面试官可能会根据环形链表的结构延申出很多问题，所以大家需要对这环形链表结构非常熟悉哦！！
本片博客就来详细的讲讲解一下 环形链表，让我们的面试变的更加顺利！！！

二、什么是环形链表？

🥝 环形链表的概念详解

环形链表是一种特殊类型的链表数据结构，其最后一个节点的"下一个"指针指向链表中的某个节点，形成一个闭环。换句话说，链表的最后一个节点连接到了链表中的某个中间节点，而不是通常情况下连接到空指针 (null)
如果大家对链表还不熟悉可以先看看这篇文章：单链表详解

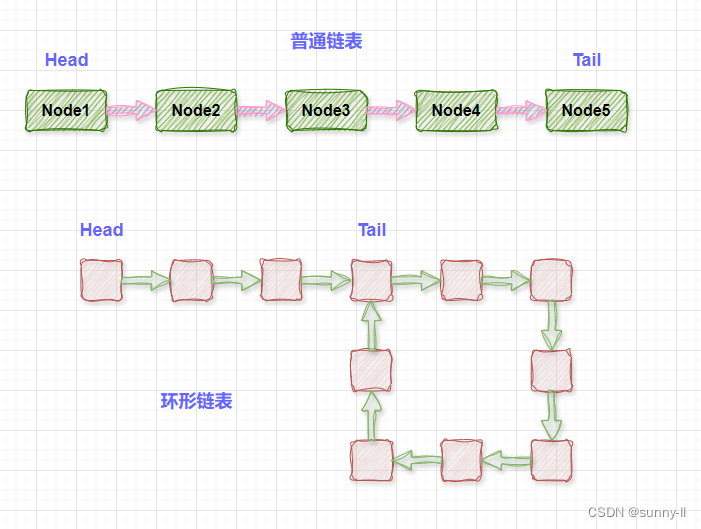
🍇 环形链表的特点

特点：
1️⃣：若一个链表带环，那么用指针一直顺着链表遍历，最终会回到某个地方。
2️⃣： 我们可以定义两个指针（快慢指针），两个指针均从表头开始同时遍历链表，快指针一次走两步，慢指针一次走一步。如果链表带环，那么快慢指针一定会相遇，否则快指针会先遍历完链表（遇到NULL）。

若是你不明白为什么链表带环，快慢指针就一定会相遇，那么你可以想想龟兔赛跑：

🍍环形链表的延申问题

1️⃣：为什么慢指针走一步，快指针走两步，他们一定会在环里面meet吗？会不会永远追不上？

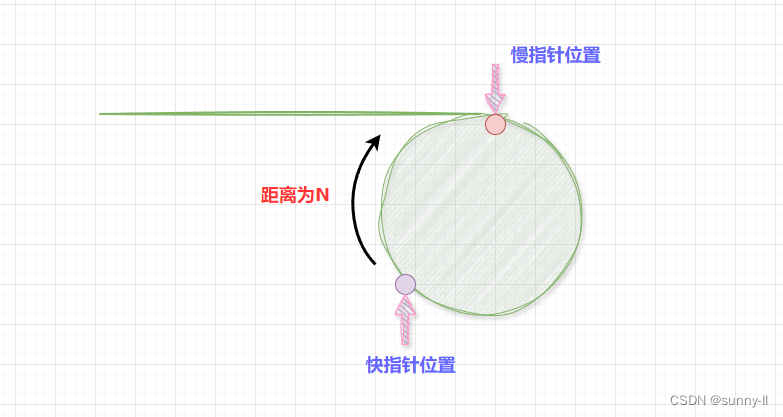
首先 慢指针和快指针，一定是快指针先进环。
随着慢指针进环，快指针已经在环了走了一段距离，走了多少和环的大小有关
假设慢指针进环的时候距离快指针距离为 N ，快指针开始追慢指针
在追击过程中，快指针往前走两步，慢指针往前走一步，每走一次它们之间的距离就缩小 1
它们之间的距离变化为 N ,N-1 ,N-2 , . . . 1 ,0 ,它们之间的距离为零就会相遇，所以一定追得上

2️⃣: 为什么一定是慢指针走一步快指针走两步？快指针能走其它步数吗？

假设慢指针进环的时候，快指针和慢指针之间的距离为 N
在追击的时候，快指针走三步，慢指针走一步，每走一次，它们之间的距离缩小 2

此时分两种情况：

若 N 为偶数，则它们之间的距离会减少到 0 相遇
若 N 为奇数，则它们之间的距离会减少到1 然后减少到 -1。减少到 -1 也就意味着它们之间的距离又变为 C - 1 (C是环的周长)

此时又分两种情况：

若 C 为奇数，则 C - 1 为偶数 ，因为它们之间的距离一次缩短 2 所以它们会相遇
若 C 为偶数，则 C - 1 为奇数 ，也就是说它们之间的距离还是奇数，它们永远不会相遇

由此可以得出结论：快指针一次不走两步，存在追不上的情况。
所以必须 ---- 每次慢指针走一步，快指针走两步

3️⃣ ：如何才能得知环口的节点是哪一个呢？

追上的相遇的过程中，慢指针的距离：L+X，快指针的距离：L+NC+X
由于不知道快指针在环里多跑了几圈，所以设了一个N，但是N肯定>=1,
因为快指针是满指针的两倍，所以2(L+X)=L+NC+X。整理可得 L= NC - X

至此，我们发现链表头到环入口的距离 L 与相遇点到环入口的距离 C-X 相差 N 个环的长度。
结论：一个指针指向链表头，一个指针指向第一次相遇点，并使两个指针的速度都为 1 ，一直前进直到它们相遇，第二次相遇的位置一定为环的入口位置。

三、高频面试题

✨环形链表

题目链接：141. 环形链表 - 力扣（LeetCode）

解题思路：

我们可以使用快慢指针法。定义步长为2的快指针和步长为1的慢指针遍历链表。我们假设链表如果存在环，则快慢指针在某一时刻一定会在环内相遇；而如果不存在环，由于快指针速度比慢指针快，因此它们永远无法相遇。

代码：

class Solution {
public:// 题目已经给出了 单链表的 节点构造bool hasCycle(ListNode *head) {// 定义两个快慢指针ListNode* slow = head;    //  每次走一步ListNode* fast = head;    //  每次走两步// 当链表 有环存在时 fast 和 fast-next 一定不会指向空// 当快指针不为空且其下一个节点也不为空时，继续循环while(fast!=nullptr && fast->next!=nullptr){slow = slow->next;fast = fast->next->next;// 相交成环if(slow == fast){return true;}}return false;}
};

疑问：为什么循环的结束条件是fast或者fast->next指向NULL？

当一个链表中有环时，fast和fast->next永远不会指向NULL
当一个链表中没有环时，fast一定会移动到链表的结尾；又因为fast一次移动两个节点，所以有两种情况：①fast移动两次后，刚好指向NULL，结束循环；②fast移动一次后就已经指向NULL，此时再进行移动，就会出现对NULL的解引用

✨环形链表II

题目链接：142. 环形链表 II - 力扣（LeetCode）

解题思路：

起初快指针速度为2，慢指针速度为1，如果快慢指针没有相遇，则返回NULL代表不存在环；如果相遇了，我们就让其中一个指针重新指向链表头，并使两个指针的速度都为1，一直前进直到它们相遇，相遇的位置一定为环的位置。这是因为从相遇点走 L 步后的位置与走C - X 步后的位置一致。

代码：

class Solution {
public:ListNode *detectCycle(ListNode *head) {// 初始化两个指针，快指针fast和慢指针slow，都指向链表头节点ListNode* slow = head;ListNode* fast = head;// 当快指针和其下一位都不为空时（即未到达链表尾部）while(fast&&fast->next){// 慢指针每次前进一步slow = slow->next;// 快指针每次前进两步fast = fast->next->next;// 如果两个指针第一次相遇while(slow==fast){// 将相遇的节点赋值给 meet变量ListNode* meet = fast;// 从头节点开始，另一个指针从相遇点开始，两者每次各前进一步// 直到两个指针再次相遇，相遇点即为环的起始节点while(head!=meet){head = head->next;meet = meet->next;}// 返回找到环的入口节点return meet;}}return NULL;}
};

✨环形链表的环长

题目描述：
给定一个链表的头节点 head ，返回链表环中环的长度。如果链表无环，则返回 0。
如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。

解题思路：

我们同样可以先使用快慢指针判断链表是否存在环，当二者第一次相遇时说明链表存在环。而当快慢指针相遇后我们再次让快慢指针进行追逐战，此时它们之间的距离为环长 C，由于每次追逐它们的距离都会缩短1，因此我们可以定义一个计数器count记录第二次相遇时所追逐的次数即为链表的环长。具体过程如下：

代码：

 struct ListNode {int val;struct ListNode* next;};
int CycleLength(struct ListNode* head)
{struct ListNode* fast = head;struct ListNode* slow = head;while (fast && fast->next) //当到达或即将到达链表尾时退出循环{//快慢指针移动fast = fast->next->next;slow = slow->next;if (fast == slow) //第一次相遇，存在环{//统计第二次相遇所追逐的次数int count = 0;do{fast = fast->next->next;slow = slow->next;count++;} while (fast != slow);//相遇了，返回追逐次数即为环长return count;}}//不存在环，返回0return 0;}

四、总结

以上就是今天要讲的内容，做题的时候，就是奔着双指针的思路进行解决的，练习这么多次现在逐渐找到了点感觉。我感觉就是双指针的关键点就是在于该怎么去移动两个指针，理清这一点之后离结果也就不远了，判断链表是否有环应该是老生常谈的一个话题了，最简单的一种方式就是快慢指针。慢指针针每次走一步，快指针每次走两步，如果相遇就说明有环，如果有一个为空说明没有环。所以就赶紧记录一下这时刻。