本文主要是介绍滑动窗口算法:巧妙玩转数据的窗外世界,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
✨✨✨学习的道路很枯燥,希望我们能并肩走下来!
文章目录
目录
文章目录
前言
一 滑动窗口是什么?
二 相关题目解析
1. 长度最小的子数组
🥳题目解析
🥳算法原理
✏️思路1 暴力枚举出所有子数组之和
✏️思路2 滑动窗口
2. 无重复字符的最长子串
🥳题目解析
🥳算法原理
✏️思路1 暴力枚举 + 哈希表
✏️思路2 滑动窗口优化+哈希表
3. 最大连续1的个数 III
🥳题目解析
🥳算法原理
✏️思路1 暴力枚举 + 计数器
✏️思路2 滑动窗口优化+计数器
4.将x减到0的最小操作数
🥳题目解析
🥳算法原理
✏️思路 滑动窗口(正难则反
5. 水果成篮
🥳题目解析
🥳算法原理
✏️思路 滑动窗口+哈希表
6. 找到字符串中所有字母异位词
🥳题目解析
🥳算法原理
✏️思路 滑动窗口+哈希表
7. 串联所有单词的字串
🥳题目解析
🥳算法原理
✏️思路 滑动窗口+哈希表编辑
8. 最小覆盖字串
🥳题目解析
🥳算法原理
✏️思路 滑动窗口+哈希表
总
前言
本篇详细介绍了滑动窗口的使用,让使用者了解滑动窗口,而不是仅仅停留在表面,更好的模拟,为了更好的使用. 文章可能出现错误,如有请在评论区指正,让我们一起交流,共同进步!
一 滑动窗口是什么?
其实就是我们前文提到的同向指针(前后指针
一般情况下,我们利用同向双指针来维护一个区间,在移动区间的过程中像一个窗口滑来滑去,因此称为滑动窗口
简而言之,滑动窗口算法在一个特定大小的字符串或数组上进行操作,而不在整个字符串和数组上操作,这样就降低了问题的复杂度,从而也达到降低了循环的嵌套深度。其实这里就可以看出来滑动窗口主要应用在数组和字符串上。
什么时候用滑动窗口?
1. 同向双指针
2. 指针不回退
二 相关题目解析
1. 长度最小的子数组
🥳题目解析
209. 长度最小的子数组 - 力扣(LeetCode)

这道题要求我们返回符合条件的子数组的最小长度,没有则返回0
🥳算法原理
✏️思路1 暴力枚举出所有子数组之和
暴力枚举出所有子数组之和,时间复杂度为O(N2)
class Solution {
public:int minSubArrayLen(int s, vector<int>& nums) {int n = nums.size();if (n == 0) {return 0;}int ans = INT_MAX;for (int i = 0; i < n; i++) {int sum = 0; //利用sum边走边++,使得不用再遍历一遍for (int j = i; j < n; j++) {sum += nums[j];if (sum >= s) {ans = min(ans, j - i + 1);break;}}}return ans == INT_MAX ? 0 : ans;}
};✏️思路2 滑动窗口
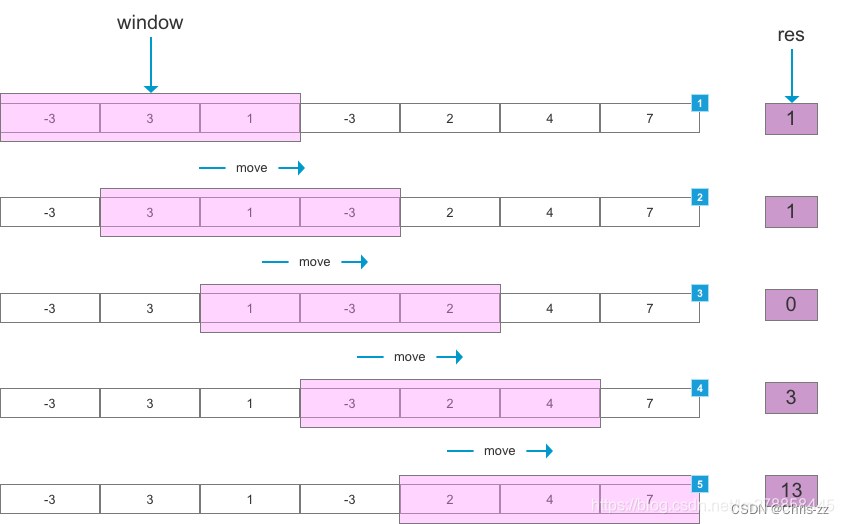
我们在暴力解法的过程中发现,有一些情况是没有必要枚举出来的(一定不符合要求
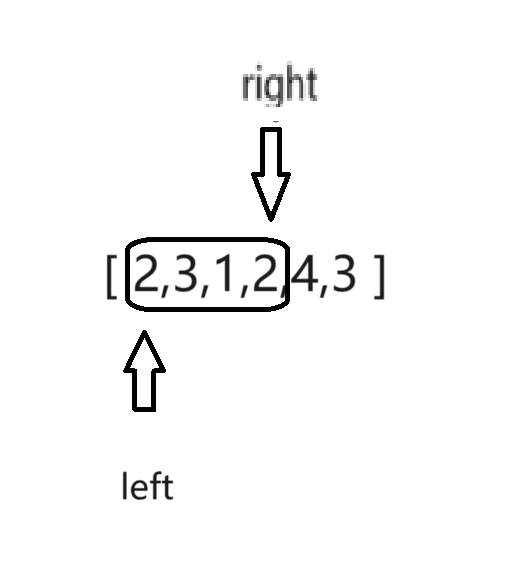
当我们移动到如图上所示时,子数组的值已经大于target,
如果我们继续扩大窗口, 子数组的值一定仍大于target,但子数组的长度不断扩大,与我们的最小子数组长度不符,因此无需枚举后面的情况。

代码解析
class Solution {
public:int minSubArrayLen(int target, vector<int>& nums) {int sum = 0, len = INT_MAX; //给最大,方便更新结果for(int left = 0,right =0;right<nums.size();right++){sum+=nums[right]; //进窗口while(sum>=target)//判断{len = min(len,right-left+1); //更新结果sum-=nums[left++]; //出窗口}}return len == INT_MAX ? 0 : len;}
};2. 无重复字符的最长子串
🥳题目解析
3. 无重复字符的最长子串 - 力扣(LeetCode)

🥳算法原理
✏️思路1 暴力枚举 + 哈希表
固定一个数,从左到右遍历,将每个数放进哈希表,遇到重复的数停止,更新数据,固定数位置右移重复上述操作
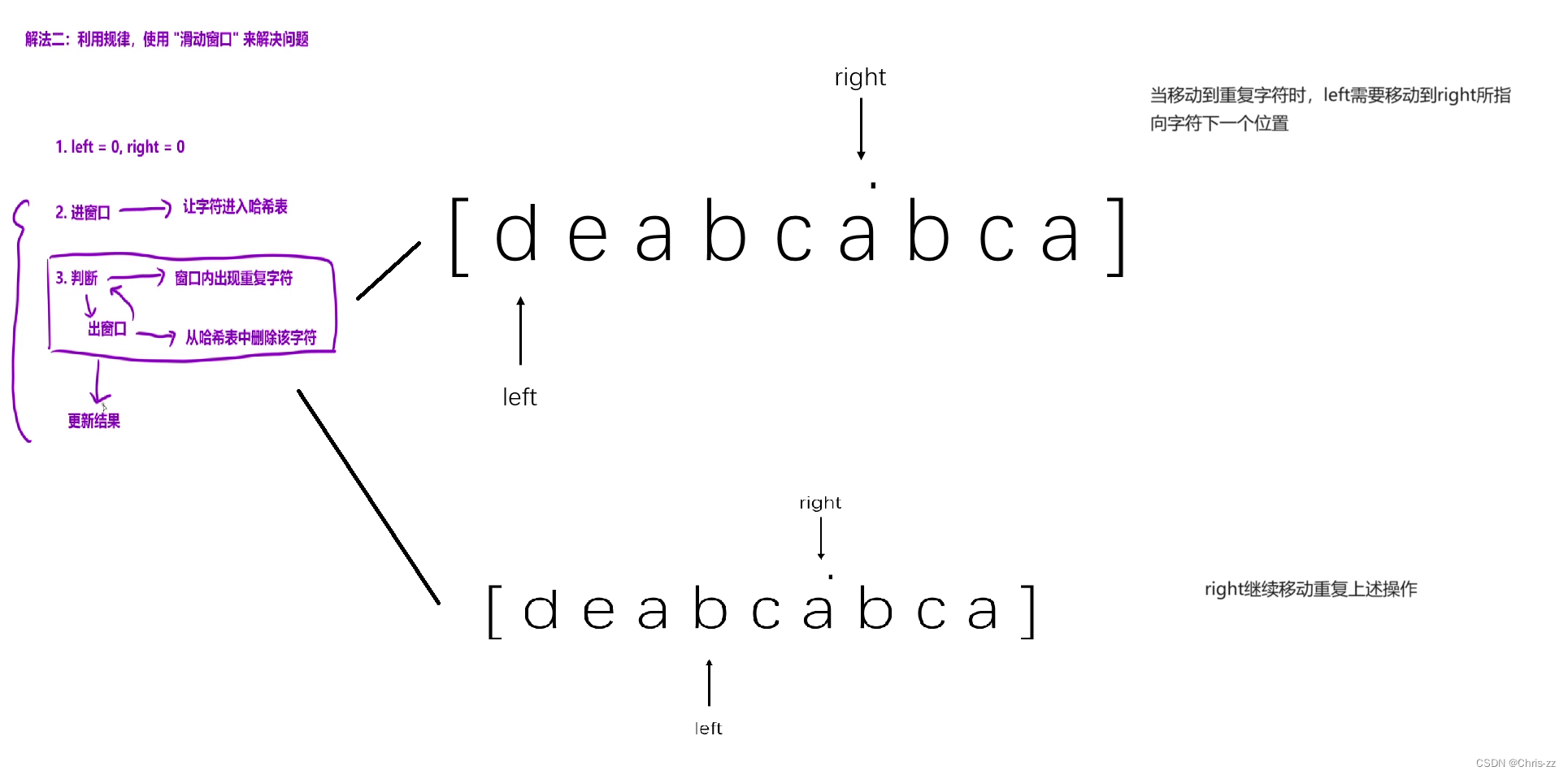
✏️思路2 滑动窗口优化+哈希表
class Solution {
public:int lengthOfLongestSubstring(string s) {int hax[128]={0}; //利用数组来模拟哈希表int left = 0, right = 0;int ret = 0;while(right<s.size()){hax[s[right]]++; //进窗口while(hax[s[right]]>1) //判断重复hax[s[left++]]--; //出窗口ret = max(ret,right-left+1); //更新结果right++; //让下一个元素进入窗口}return ret;}
};3. 最大连续1的个数 III
🥳题目解析
1004. 最大连续1的个数 III - 力扣(LeetCode)

🥳算法原理
✏️思路1 暴力枚举 + 计数器
for(int i = 0 ;i<nums.size();i++)
{for(int j = i;j<nums.size();j++){//...zero>k}
}✏️思路2 滑动窗口优化+计数器
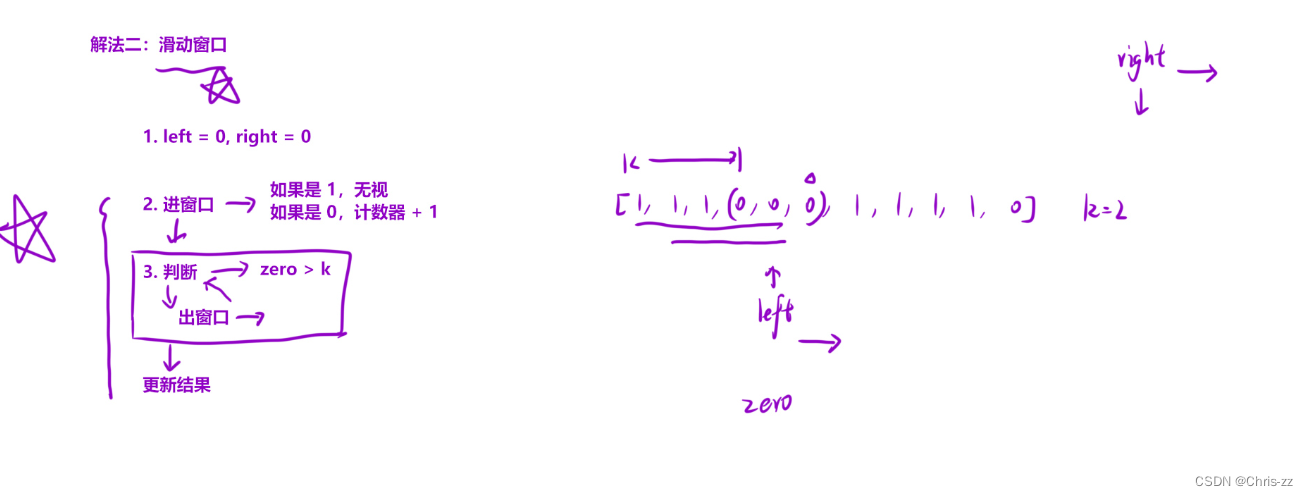
class Solution {
public:int longestOnes(vector<int>& nums, int k) {int ret = 0;for(int left = 0,right = 0,zero = 0;right<nums.size();right++){if(nums[right] == 0) //进窗口zero++;while(zero>k) //判断{if(nums[left++]==0) //出窗口zero--;}ret = max(ret,right-left+1); //更新结果}return ret;}
};4.将x减到0的最小操作数
🥳题目解析

🥳算法原理
✏️思路 滑动窗口(正难则反

class Solution {
public:int minOperations(vector<int>& nums, int x) {int sum = 0;for(auto&e : nums)sum+=e;int tmp = 0, len = -1;int target = sum - x;if(target<0)return -1;for(int left = 0 ,right = 0 ;right<nums.size();right++){tmp+=nums[right];while(tmp>target){tmp-=nums[left++];}if(tmp == target)len = max(len,right - left + 1);}if(len == -1)return len;else return nums.size()-len;}
};5. 水果成篮
904. 水果成篮 - 力扣(LeetCode)
🥳题目解析

🥳算法原理
✏️思路 滑动窗口+哈希表
 因为题目中提到
因为题目中提到
1 <= fruits.length <= 105
因此我们可以用数组来代替哈希表
class Solution {
public:int totalFruit(vector<int>& fruits) {int hash[100001] = {0};//统计窗口内出现了多少种水果int ret = 0;for(int left = 0,right = 0, kinds = 0;right<fruits.size();right++){if(hash[fruits[right]] == 0)kinds++;hash[fruits[right]]++; //进窗口while(kinds >2) //判断{//出窗口hash[fruits[left]]--;if(hash[fruits[left]] == 0)kinds--;left++;}//更新结果ret = max(ret,right - left +1);}return ret;}
};6. 找到字符串中所有字母异位词
438. 找到字符串中所有字母异位词
🥳题目解析
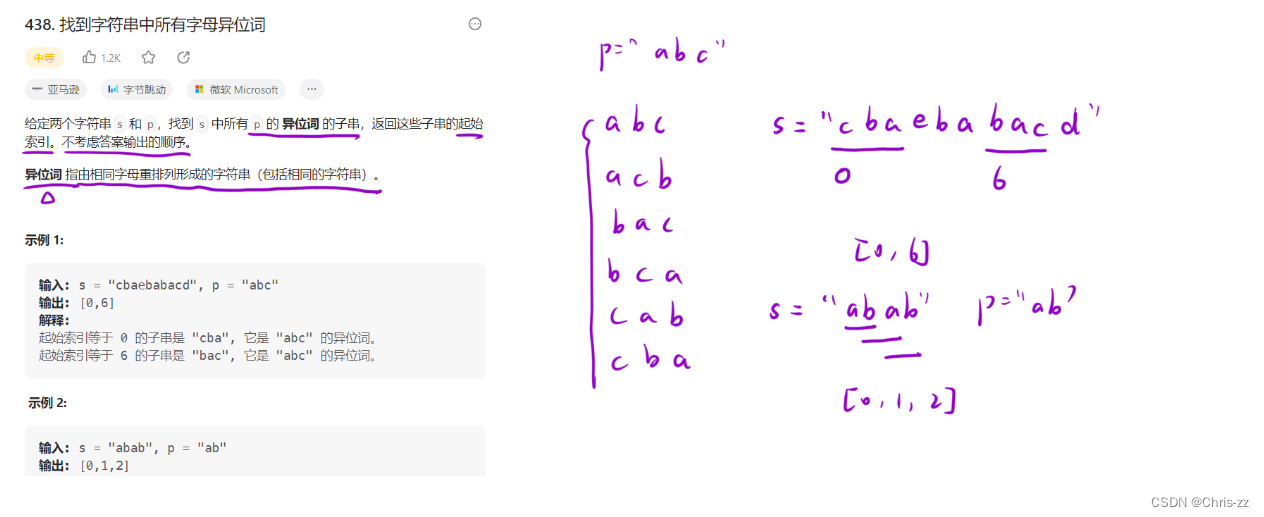
🥳算法原理
✏️思路 滑动窗口+哈希表

class Solution {
public:bool check(int s1[],int s2[]){for(int i = 0;i<26;i++){if(s1[i]!=s2[i])return false;}return true;}vector<int> findAnagrams(string s, string p) {int hash1[26] = {0};int hash2[26] = {0};vector<int> result;for(int i = 0;i<p.size();i++){hash1[p[i]-'a']++;}for(int left = 0,right = 0;right<s.size();right++){hash2[s[right]-'a']++;if(right-left+1>p.size()){hash2[s[left]-'a']--;left++;}if(check(hash1,hash2))result.push_back(left);}return result;}
};这里我们发现我们每次都要频繁的进入check函数进行检查,时间复杂度为26*n
我们可以对检查这一步骤进行优化

class Solution {
public:vector<int> findAnagrams(string s, string p) {int hash1[26] = {0}; //统计字符串p中每个字符出现个数for(auto&e : p) hash1[e-'a']++;int hash2[26] = {0};//统计窗口中每个字符出现个数vector<int> ret;for(int left = 0,right = 0,count = 0;right<s.size();right++) //count窗口中有效字符个数{char in = s[right];if(++hash2[in-'a']<=hash1[in-'a']) count++; //进窗口+维护countif(right - left + 1 >p.size()) //判断{char out = s[left++];if(hash2[out-'a']--<=hash1[out-'a']) count--; //出窗口+维护count}//更新结果if(count == p.size()) ret.push_back(left);}return ret;}
};7. 串联所有单词的字串
30. 串联所有单词的子串 - 力扣(LeetCode)
🥳题目解析

此题是「438. 找到字符串中所有字母异位词」的进阶版。不同的是第 438 题的元素是字母,而此题的元素是单词。可以用类似的方法的滑动窗口来解这题。
🥳算法原理
✏️思路 滑动窗口+哈希表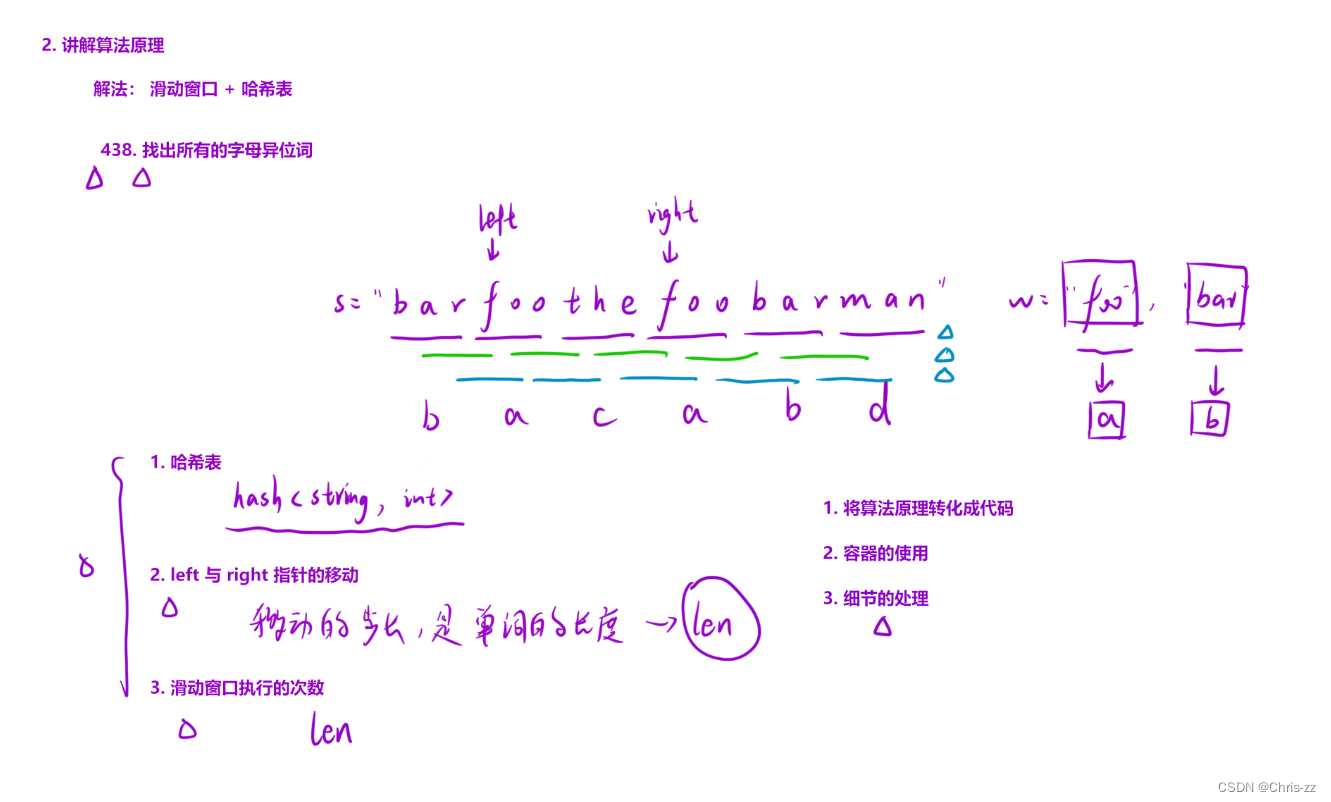
class Solution {
public:vector<int> findSubstring(string s, vector<string>& words) {vector<int> ret;unordered_map<string,int> hash1; //保存words里面所有单词的频率for(auto& e : words) hash1[e]++;int len = words[0].size(), n = words.size();for(int i = 0;i < len; i++) //执行len次{unordered_map<string,int> hash2; //保护窗口内单词的频率for(int left = i,right = i, count = 0;right+len<=s.size();right+=len){//进窗口+维护countstring in = s.substr(right,len);if(++hash2[in]<=hash1[in]) count++;//判断if(right-left+1>len*n){//出窗口+维护countstring out = s.substr(left,len);if(hash2[out]--<=hash1[out]) count--;left+=len;}//更新结果if(count == n) ret.push_back(left);} }return ret;}
};小细节优化:
if(++hash2[in]<=hash1[in]) count++;执行这段代码时,hash1哈希表未必有对应的单词in,这时候编译器会向hash1创建一个in,使得时间复杂度增加
优化后的代码
class Solution {
public:vector<int> findSubstring(string s, vector<string>& words) {vector<int> ret;unordered_map<string,int> hash1; //保存words里面所有单词的频率for(auto& e : words) hash1[e]++;int len = words[0].size(), n = words.size();for(int i = 0;i < len; i++) //执行len次{unordered_map<string,int> hash2; //保护窗口内单词的频率for(int left = i,right = i, count = 0;right+len<=s.size();right+=len){//进窗口+维护countstring in = s.substr(right,len);if(hash1.count(in)&&++hash2[in]<=hash1[in]) count++;//判断if(right-left+1>len*n){//出窗口+维护countstring out = s.substr(left,len);if(hash1.count(out)&&hash2[out]--<=hash1[out]) count--;left+=len;}//更新结果if(count == n) ret.push_back(left);} }return ret;}
};8. 最小覆盖字串
76. 最小覆盖子串 - 力扣(LeetCode)
🥳题目解析

🥳算法原理
✏️思路 滑动窗口+哈希表
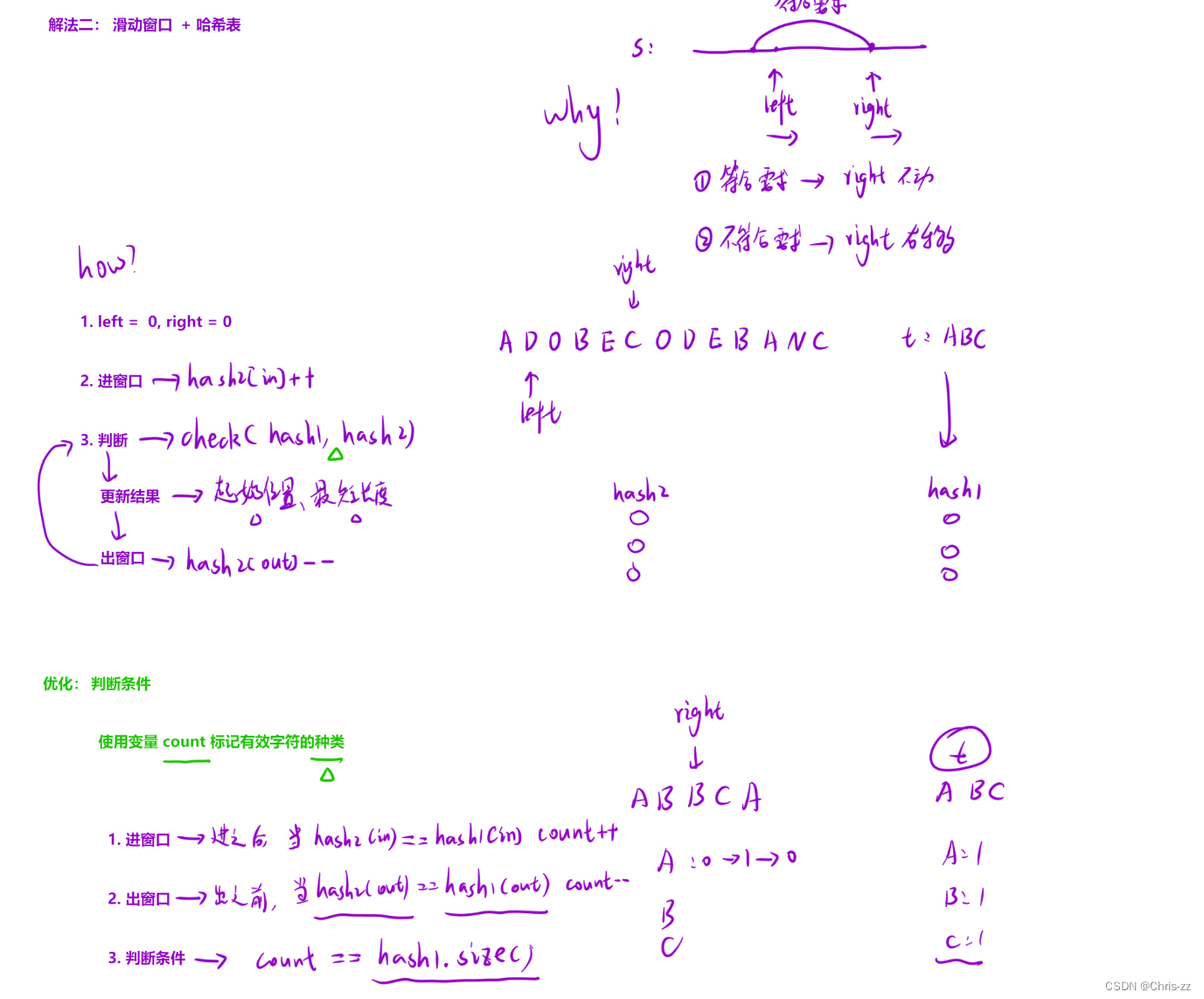
class Solution {
public:string minWindow(string s, string t) {int hash1[128] = {0};int kinds = 0;for(auto& ch : t){if(hash1[ch]==0) kinds++;hash1[ch]++;}int hash2[128] = {0};int minlen = INT_MAX, begin = -1;for(int left = 0,right = 0,count = 0;right<s.size();right++){char in = s[right];if(++hash2[in] == hash1[in]) count++;while(count == kinds){if(right-left+1<minlen){minlen = right-left+1;begin = left;}char out = s[left++];if(hash2[out]-- == hash1[out]) count--;}}if(begin == -1) return "";else return s.substr(begin,minlen);}
};总结
✨✨✨各位读友,本篇分享到内容是否更好的让你理解滑动窗口算法,如果对你有帮助给个👍赞鼓励一下吧!!
🎉🎉🎉世上没有绝望的处境,只有对处境绝望的人。
感谢每一位一起走到这的伙伴,我们可以一起交流进步!!!一起加油吧!!
这篇关于滑动窗口算法:巧妙玩转数据的窗外世界的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





