【数据结构（邓俊辉）学习笔记】图04——双连通域分解

本文主要是介绍【数据结构（邓俊辉）学习笔记】图04——双连通域分解，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

0. 概述

学习下双连通域分解，这里略微有一点点难，这个算是DFS算法的非常非常经典的应用，解决的问题也非常非常有用。

1 关节点与双连通域

连通性很好理解，两个点在图中只要有一条路径，不管是无向的还是有向的，只要互相可达，就说他们是连通的。但有的时候会要求更严些，不仅要保证自己和某些地方的连通，还要保证某个区域不会变成独立的，另一个角度可以从关节点来理解。

明确下几个术语

考查无向图G。若删除顶点v后G所包含的连通域增多，则v称作切割节点（cut vertex）或关节点（articulation point）。
~  
如图C即是一个关节点——它的删除将导致连通域增加两块。反之，不含任何关节点的图称作双连通图。任一无向图都可视作由若干个极大的双连通子图组合而成，这样的每一子图都称作原图的一个双连通域（bi-connected component）。
~  
例如右上图中的无向图，可分解为右下图所示的三个双连通域。

任何一张连通的无向图都存在着若干个关键点，而且以这些关键点为界，可以将其分割为若干个双连通部分——BCC分量。

较之其它顶点，关节点更为重要。在网络系统中它们对应于网关，决定子网之间能否连通。在航空系统中，某些机场的损坏，将同时切断其它机场之间的交通。故在资源总量有限的前提下，找出关节点并重点予以保障，是提高系统整体稳定性和鲁棒性的基本策略。

那么怎么计算？给一个任意的图，如何将其分解为一个一个又一个BCC分量呢？作为查找结果的副产品——关键点，怎么得到？

2 蛮力算法

由其定义，可直接导出蛮力算法大致如下：

1. 首先，通过BFS或DFS搜索统计出图G所含连通域的数目；
2. 然后逐一枚举每个顶点v，暂时将其从图G中删去，并再次通过搜索统计出图G{v}所含连通域的数目。
3. 于是，顶点v是关节点，当且仅当图G{v}包含的连通域多于图G。
   
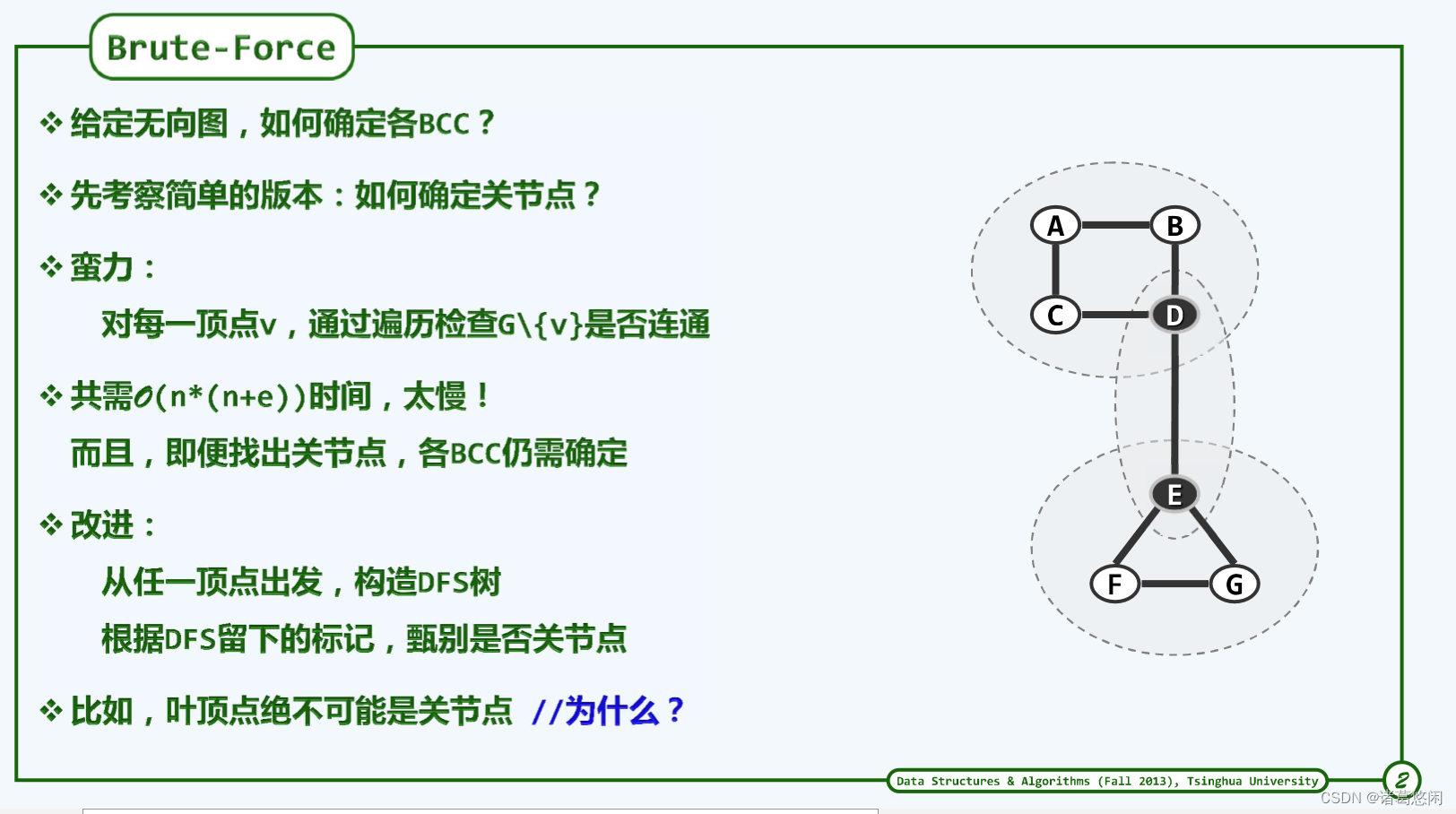
   这一算法需执行n趟搜索，耗时O(n(n + e))，如此低的效率无法令人满意。

3 可行算法

经DFS搜索生成的DFS树，表面上看似乎“丢失”了原图的一些信息，但实际上就某种意义而言，依然可以提供足够多的信息。

• 先分析下根节点 情况
  

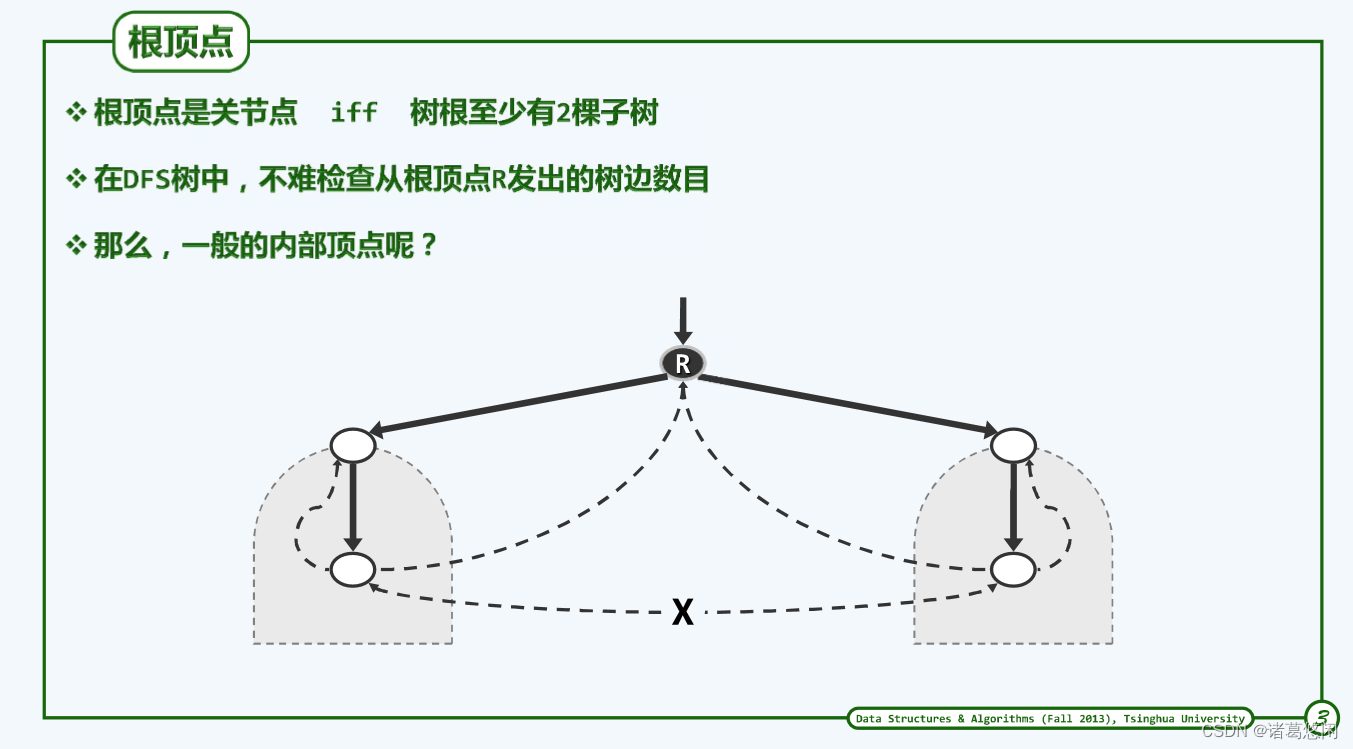
DFS树中的叶节点，绝不可能是原图中的关节点

此类顶点的删除既不致影响DFS树的连通性，也不致影响原图的连通性。

此外，DFS树的根节点若至少拥有两个分支，则必是一个关节点。

如上图，在原无向图中，根节点R的不同分支之间不可能通过跨边相联（算法中为什么讨论cross edge？因为讨论的是有向图），R是它们之间唯一的枢纽。
~  

因此，这里也得出个结论：在无向图的DFS中是不可能有cross edge和forward edge，只有back word 回向边。
~  
反之，若根节点仅有一个分支，则与叶节点同理，它也不可能是关节点。

• 那么，又该如何甄别一般的内部节点是否为关节点呢？
  
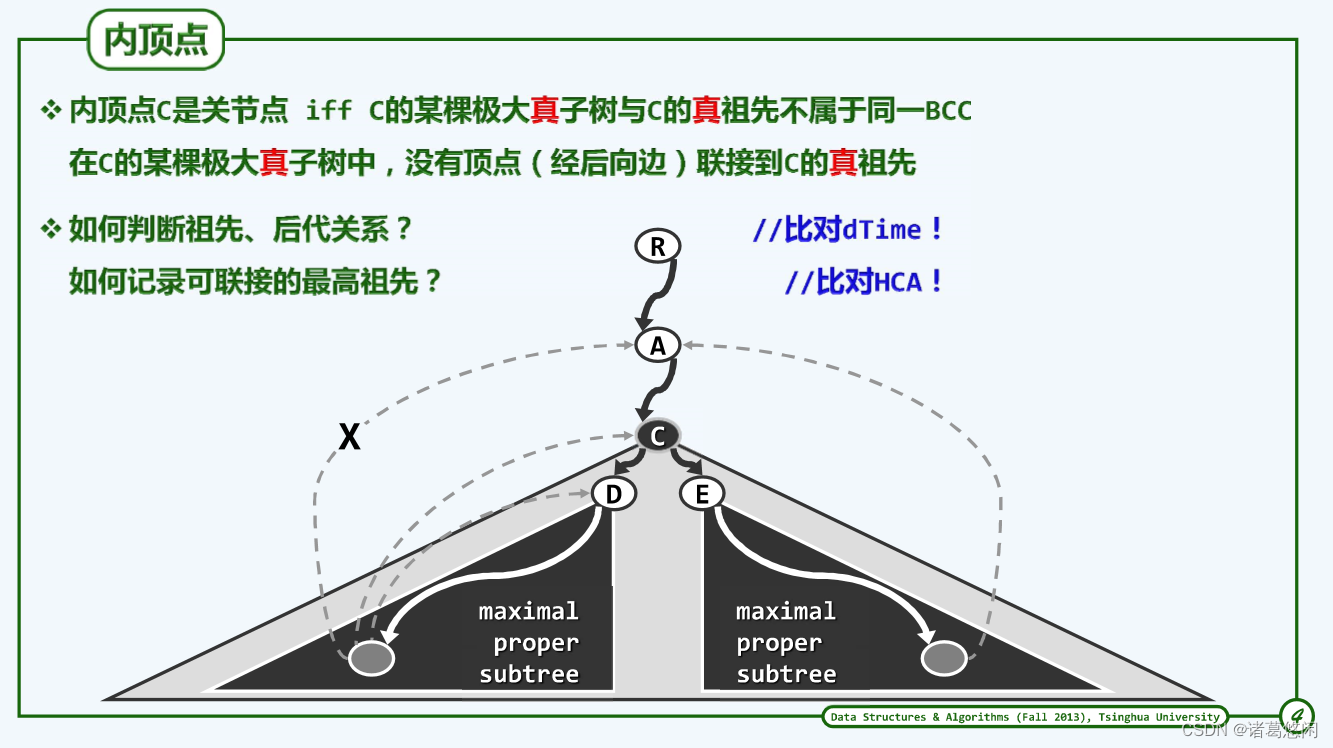
  考查上图中的内部节点C。若节点C的移除导致其某一棵（比如以D为根的）真子树与其真祖先（比如A）之间无法连通，则C必为关节点。反之，若C的所有真子树都能（如以E为根的子树那样）与C的某一真祖先连通，则C就不可能是关节点。

以D为根的真子树经过一系列访问后，会生成一系列tree edge和back edge，关键在于back edge。形象来说，若back edge往上指的不是那么高，准确来讲，不会高过父亲C，则C就是关键点。因为C若消失，则以D为根的真子树就会变成孤岛。

当然，在原无向图的DFS树中，C的真子树只可能通过后向边与C的真祖先连通。因此，只要在DFS搜索过程记录并更新各顶点v所能（经由后向边）连通的最高祖先（highest connected ancestor, HCA）hca[v]，即可及时认定关节点，并报告对应的双连通域。

以E为根的真子树中的back edge往上指的更高，准确来讲，高过父亲C，则C就不是关键点。因为C若消失，则以E为根的真子树也会通过back edge保持连通。

因此通过遍历需要得到很重要指标 dTime 和 HCA，算法大体框架

• 由括号引理： dTime越小的祖先，辈份越高
• DFS过程中，一旦发现后向边（v,u） ~~~~      即取：hca(v) = min( hca(v) , dtime(u) )
• DFS(u) 完成并返回v时 ~~~~      若有：hca(u) < dTime(v) ~~~~      即取：hca(v) = min( hca(v), hca(u) ) ~~~~      否则，即可判定：v系关节点，且 {v} + subtree(u) 即为一个BCC。

• 那么如何实现？

4 实现

算法来看就是典型的DFS，这里改个名字叫BCC，这里利用闲置的fTime充当hca。

• 看下u分别有哪些状态需要处理？
  首先看下UNDISCOVERED状态，既tree edge
  
  在从顶点u处深入到遍历返回后之间的代码逻辑与DFS几乎一致，当遍历返回后，v的hca便已确定。故DFS搜索在顶点v的孩子u处返回之后，通过比较hca[u]与dTime[v]的大小，即可判断v是否关节点。

1. 若hca[u] ≥ dTime[v]，则说明u及其后代无法通过后向边与v的真祖先连通，故v为关节点。既然栈S存有搜索过的顶点，与该关节点相对应的双连通域内的顶点，此时都应集中存放于S顶部，故可依次弹出这些顶点。v本身必然最后弹出，作为多个连通域的联接枢纽，它应重新进栈。
2. 反之若hca[u] < dTime[v]，则意味着u可经由后向边连通至v的真祖先。果真如此，则这一性质对v同样适用，故有必要将hca[v]，更新为hca[v]与hca[u]之间的更小者。

再看下DISCOVERED 和VISITED（这个状态只有有向边才有，这里可不关注，只是为了和DFS作对比）

当然，每遇到一条后向边(v, u)，也需要及时地将hca[v]，更新为hca[v]与dTime[u]之间的更小者，以保证hca[v]能够始终记录顶点v可经由后向边向上连通的最高祖先。

5 示例

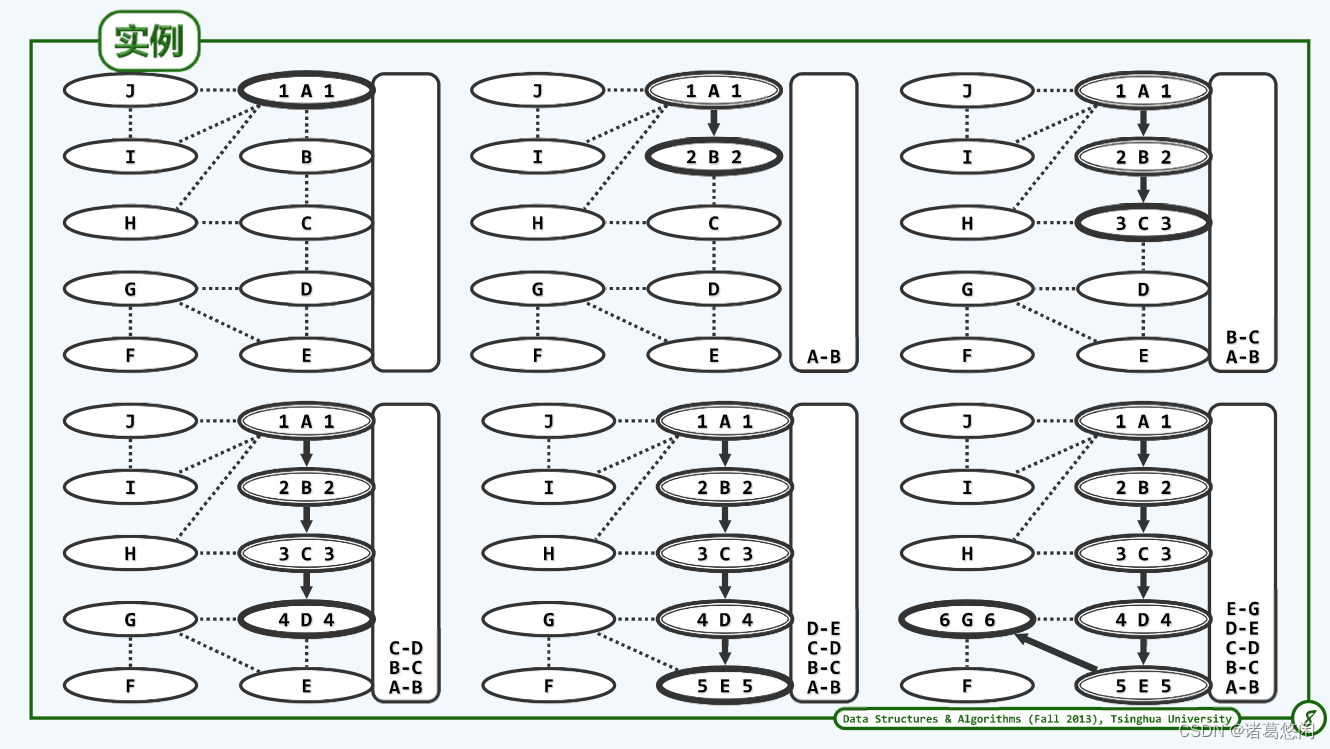
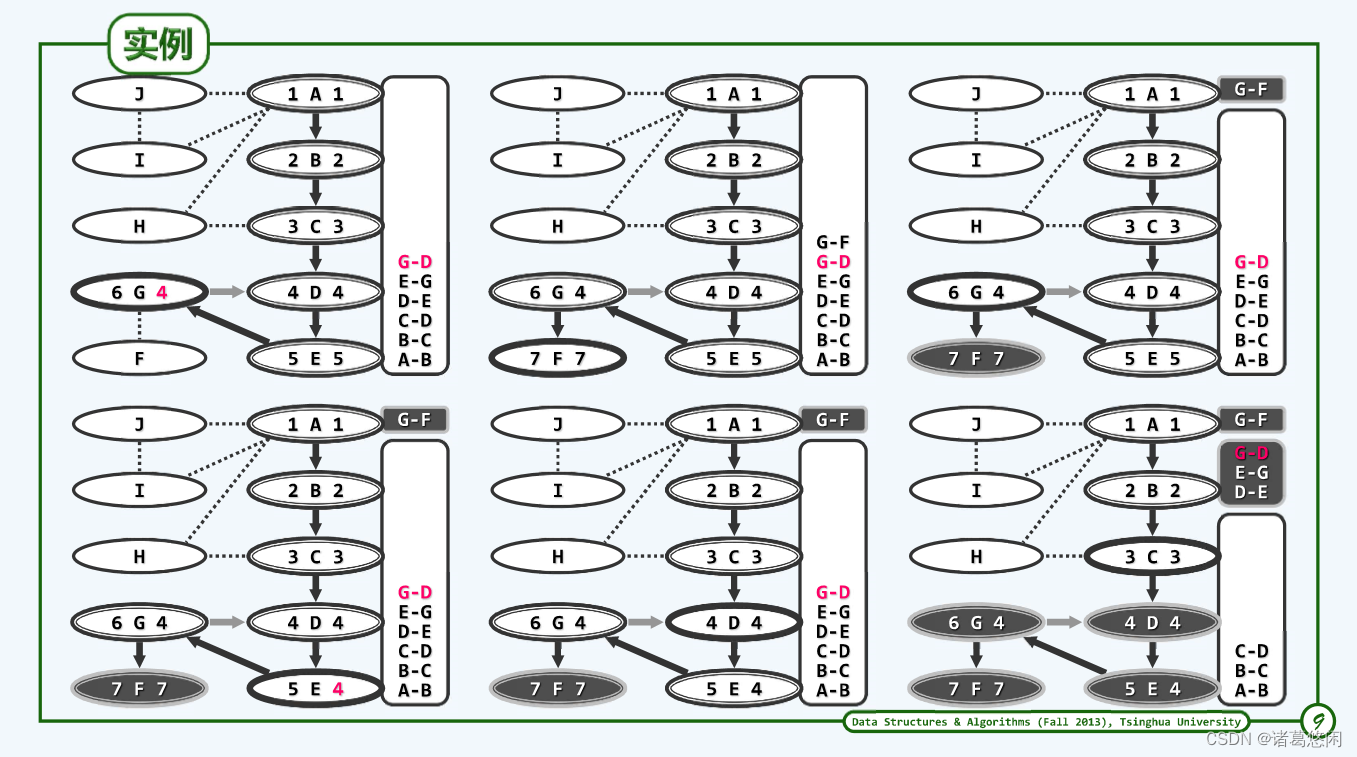
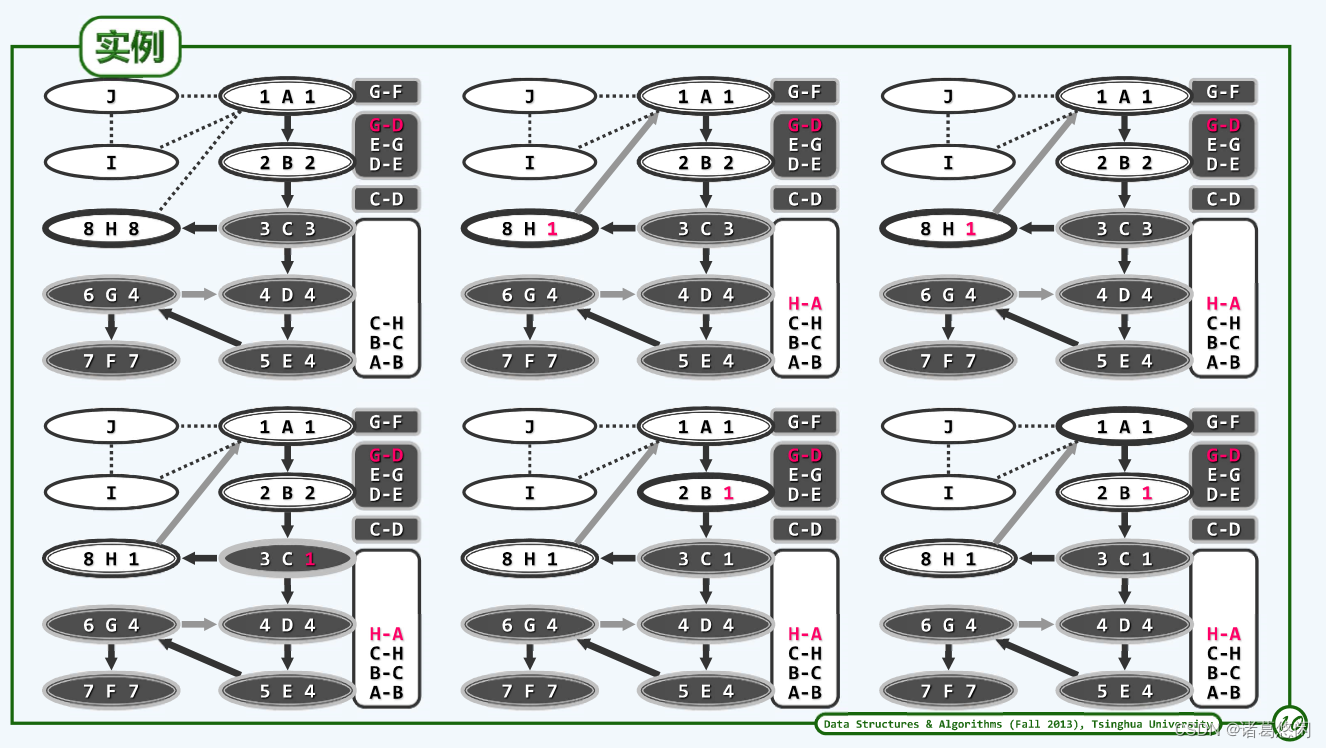
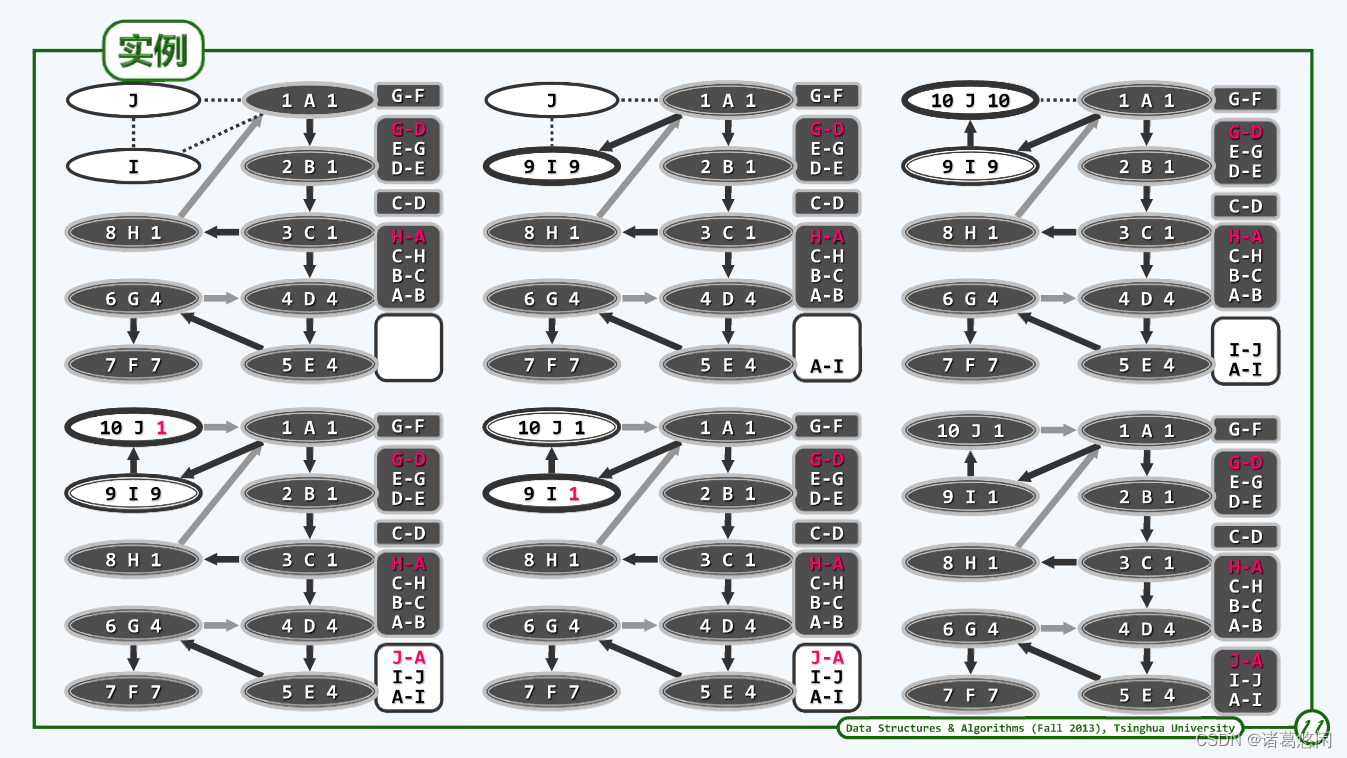
6 复杂度

与基本的DFS搜索算法相比，这里只增加了一个规模O(n)的辅助栈，故整体空间复杂度仍为O(n + e)。时间方面，尽管同一顶点v可能多次入栈，但每一次重复入栈都对应于某一新发现的双连通域，与之对应地必有至少另一顶点出栈且不再入栈。因此，这类重复入栈操作不会超过n次，入栈操作累计不超过2n次，故算法的整体运行时间依然是O(n + e)。

这篇关于【数据结构（邓俊辉）学习笔记】图04——双连通域分解的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---