本文主要是介绍VBA高级应用30例应用2实现在列表框内及列表框间实现数据拖动,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
《VBA高级应用30例》(版权10178985),是我推出的第十套教程,教程是专门针对高级学员在学习VBA过程中提高路途上的案例展开,这套教程案例与理论结合,紧贴“实战”,并做“战术总结”,以便大家能很好的应用。教程的目的是要求大家在实际工作中分发VBA程序,写好的程序可以升级。本套教程共三册三十个专题,本讲的内容是:VBA高级应用30例应用2实现在列表框内及列表框间实现数据拖动:窗体及模块的实现过程
【分享成果,随喜正能量】 修行,不是让你什么都顺,而是让你知道为什么不顺?心里执着的多,磨难就越多,越想得到什么,就会失去什么。修行,不是等待菩萨来救赎,
而是需要自渡,去向内求,提升自己的内在认知,修正自己的贪、嗔、痴、慢、疑,
圆满自己,利益他人。。
应用2 在列表框内及列表框间实现数据拖动
3 窗体及模块的实现过程
这部分我们要完成窗体及其模块的构建,这个构建过程中我们要完成窗体的初始化及类的实例化。
1) 对于是否允许列表框内移动的设置,这是通过DragWithin1,和DragWithin2参数的设置来完成的,这两个参数的值通过两个CheckBox的点击实现,代码如下:
Private Sub CheckBox1_Click()
mcDragDrop.DragWithin1 = Me.CheckBox1.Value
End Sub
Private Sub CheckBox2_Click()
mcDragDrop.DragWithin2 = Me.CheckBox2.Value
End Sub
代码的截图:

2)窗体的初始化及实例化类。在窗体的初始化过程中我们要完成列表框的初始化赋值及类的实例化过程。我们看下面的代码。
'窗体的初始化
Private Sub UserForm_Initialize()
Dim i As Long
'向列表框中添加数据
With ThisWorkbook.Sheets("sheet1")
For i = 1 To Int(.Range("a1").End(xlDown).Row / 2)
Me.ListBox1.AddItem "Item " & .Range("a" & i)
Next
For i = Int(.Range("a1").End(xlDown).Row / 2) + 1 To .Range("a1").End(xlDown).Row
Me.ListBox2.AddItem "Item " & .Range("a" & i)
Next
End With
'实例化类
Set mcDragDrop = New clsDragDrop
With mcDragDrop
'类对象列表框与窗体列表框关联
Set mcDragDrop.ListBox1 = Me.ListBox1
Set mcDragDrop.ListBox2 = Me.ListBox2
End With
'在两个列表框中启用拖放
Me.CheckBox1.Value = True
Me.CheckBox2.Value = True
'列表框中允许多选
Me.ListBox1.MultiSelect = fmMultiSelectMulti
Me.ListBox2.MultiSelect = fmMultiSelectMulti
End Sub
代码的截图:

[待续]

我20多年的VBA实践经验,全部浓缩在下面的各个教程中:
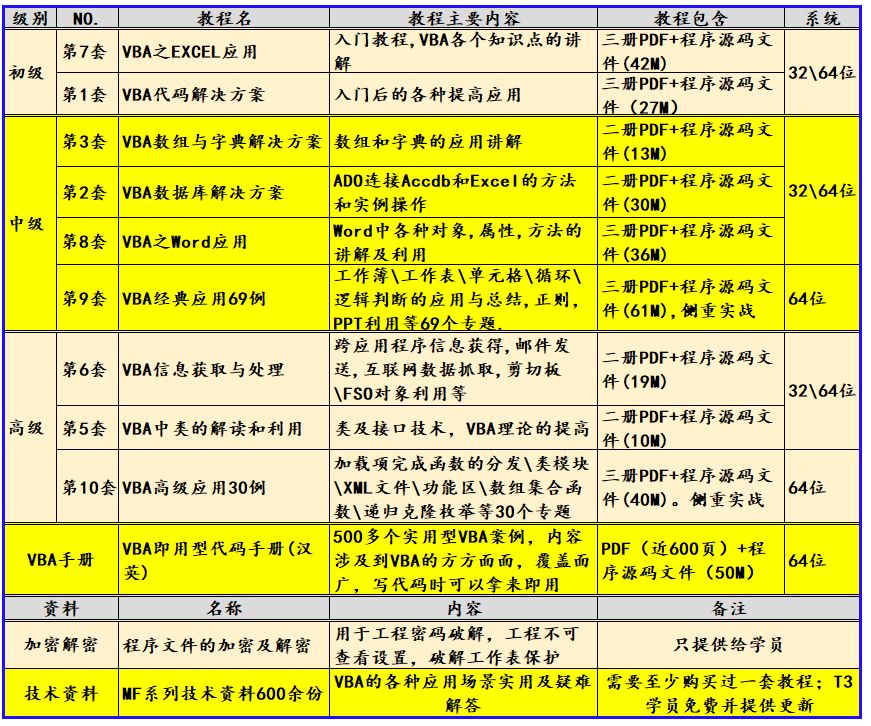
这篇关于VBA高级应用30例应用2实现在列表框内及列表框间实现数据拖动的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







