秒解-今年高考数学压轴题，你不知道有多爽！附带：计算机程序验证结果

本文主要是介绍秒解-今年高考数学压轴题，你不知道有多爽！附带：计算机程序验证结果，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

同步的公众号文章在此，今年高考数学-压轴题原来可以秒解啊！附带：计算机程序验证结果没错，其实高考数学-压轴题其实可以秒解的呀~https://mp.weixin.qq.com/s/4M50qP9MFwJOS9OpeyxvSg

没错，其实新课标I数学-压轴题其实可以秒解的呀~

课标I的高考压轴题的截图

解析：

其实你内心想这个数列完全可以使1、2、3、4、5、6。

1、使数列成为可分数列的(i,j)为

        (1,2)：剩下的 3456 为等差数列
        (1,6)：剩下的 2345 为等差数列
        (5,6)：剩下的 1234 为等差数列
2、当m=3时，这个自己拜拜手指头，也是可以得出。也是送分题了。

(2,13)：剩下的 1 4 7 10、3 6 9 12、5 8 11 14 为等差数列
当数列的m值为：3时：使数列成为可分数列的(i,j)为：

(1,2)、(1,6)、(1,10)、(1,14)、(2,9)、(2,13)、(5,6)、(5,10)、(5,14)(6,13)、(9,10)、(9,14)、(13,14)

那么m>3呢，那毫无疑问，其实大于的m数列都是原汁原味的数列，都没变过。

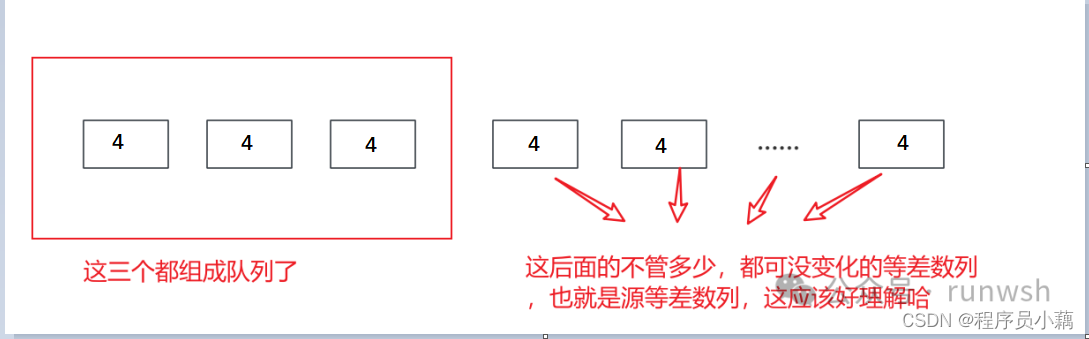
3、其实出卷老师真的很好很体贴呢。m=1、m=2、m=3。这几种情况都慢慢引导你去组合。

其实有上面的第一问和第二问就可以知道。分为两种情况的了，1、剩下的等差数列的差值和源数列的差值一致。2、剩下的等差数列的差值是源数列的差值倍数关系。数列出卷老师很照顾我们的勒。

首先：1,2......,4m+2 组成的数列均为step为1的等差数列。这个就是逆向思维了，先默认他们是排列的m组队列。 --这个有点像你们平时打的麻将，放入两个丢弃的麻将然后合起来就是源等差数列了 $\underbrace{4,4,4,4,4,\cdots,4}_M$

1、如上图大家现在就理解成把 i、j 插入到这个箱子的空隙中。

2、注意：m个数列是有m+1的空隙的哦，所以 i 有M+1次机会，而 i 插入缝隙后。j 就有M+2次机会了。所以就有 $\frac{1}{2} (\mathrm{C}_{M+1}^1 +\mathrm{C}_{M+2}^1)$ ，这里乘以1/2那是会相同的两遍，因为规定 i<j 。

其次一种情况：1,2......,4m+1 组成的数列均为step不为1的等差数列。从出卷人让我们计算可得出 2 、 2+4m 、2+4(m+1) 这几种情况只需要找两种即可满足了。那以2倍来算。可以取的方式就是 $\mathrm{C}_{M}^2$ 。仅当M>1的时候成立。--不太明白的可以参考：m=2 时有：(2,9)。m=3时有：（2,9）、（2,13）、（9,13）。那当m=k时，必定有 $\underbrace{2,9,13,17,\cdots,4(M-2)+2}_M$ 也是当且仅当M>1该等式成立。
因为当m=1时，这个概率为 $P=\frac{3}{\mathrm{C}_6^2 } = \frac{1}{5} > \frac{1}{8}$ ，当然满足的咯。

综上可秒出答案

得出的种数为： $\frac{1}{2}(\mathrm{C}_{M+1}^1 *\mathrm{C}_{M+2}^1 ) + \mathrm{C}_M^2 = M^{2}+M+1$

那概率就是

$\frac{M^2+M+1}{\mathrm{C}_{M+2}^2}$ = $\frac{M^2+M+1}{\mathrm{C}_{M+2}^2}=\frac{1}{8} ( 1+ \frac{0.75M+0.875}{M^2+0.75M+0.125})>1/8$

那step1+step2的都大于1/8的了，那就不用看step3的了。

附加：

计算机计算出来的结果

当数列的m值为：1时：使数列成为可分数列的(i,j)为：	(1,2)、(1,6)、(5,6);当数列的m值为：2时：使数列成为可分数列的(i,j)为：	(1,2)、(1,6)、(1,10)、(2,9)、(5,6)、(5,10)、(9,10);当数列的m值为：3时：使数列成为可分数列的(i,j)为：	(1,2)、(1,6)、(1,10)、(1,14)、(2,9)、(2,13)、(5,6)、(5,10)、(5,14)、(6,13)、(9,10)、(9,14)、(13,14);当数列的m值为：4时：使数列成为可分数列的(i,j)为：	(1,2)、(1,6)、(1,10)、(1,14)、(1,18)、(2,9)、(2,13)、(2,17)、(5,6)、(5,10)、(5,14)、(5,18)、(6,13)、(6,17)、(9,10)、(9,14)、(9,18)、(10,17)、(13,14)、(13,18)、(17,18);当数列的m值为：5时：使数列成为可分数列的(i,j)为：	(1,2)、(1,6)、(1,10)、(1,14)、(1,18)、(1,22)、(2,9)、(2,13)、(2,17)、(2,21)、(5,6)、(5,10)、(5,14)、(5,18)、(5,22)、(6,13)、(6,17)、(6,21)、(9,10)、(9,14)、(9,18)、(9,22)、(10,17)、(10,21)、(13,14)、(13,18)、(13,22)、(14,21)、(17,18)、(17,22)、(21,22);当数列的m值为：6时：使数列成为可分数列的(i,j)为：	(1,2)、(1,6)、(1,10)、(1,14)、(1,18)、(1,22)、(1,26)、(2,9)、(2,13)、(2,17)、(2,21)、(2,25)、(5,6)、(5,10)、(5,14)、(5,18)、(5,22)、(5,26)、(6,13)、(6,17)、(6,21)、(6,25)、(9,10)、(9,14)、(9,18)、(9,22)、(9,26)、(10,13)、(10,17)、(10,21)、(10,25)、(13,14)、(13,18)、(13,22)、(13,26)、(14,17)、(14,21)、(14,25)、(17,18)、(17,22)、(17,26)、(18,25)、(21,22)、(21,26)、(25,26);

破解程序：

package com.runwsh.sgg;import org.springframework.beans.BeanUtils;import java.util.*;/*** 设 m 为正整数,数列 a1,42,·,Q4m+2 是公差不为0 的等差数列, 若从中删去两项 q¡和 a¡(i < j)后剩余的 4m 项可被平均分为 m 组, 且每组的 4 个数都能构成等差数列, 则称数列 Q1,a2,…,a4m+2 是(i,j)一可分数列.* (1)写出所有的(i,j),1 ≤i<j≤ 6,使数列 a1,a2,···,6 是(i,j)- 可分数列;* (2)当m ≥3 时,证明: 数列 a1,q2,··,a4m+2 是(2,13)- 可分数列;* (3)从 1,2,·…·,4m +2 中一次任取两个数讠和 j(i< j),记数列 a1,a2,…,a4+2是(i,j)- 可分数列的概率为 P„ 证明: P„ > 1/8*/
public class ArithmeticSequence {public static Set<String> canFormArithmeticSequences(List<Integer> nums) {Set<String> sequences = new HashSet<>();if (nums == null || nums.size() % 4 != 0) {return sequences; // 数组长度必须是4的倍数}for (int i = 0; i < nums.size() - 3; i++) {for (int j = i + 1; j < nums.size() - 2; j++) {for (int k = j + 1; k < nums.size() - 1; k++) {for (int l = k + 1; l < nums.size(); l++) {int a = nums.get(i), b = nums.get(j), c = nums.get(k), d = nums.get(l);if (isArithmeticSequence(a, b, c, d)) {boolean flag=false;if (nums.size()>4) {nums.remove(i);nums.remove(j-1);nums.remove(k-2);nums.remove(l-3);flag=true;}else {sequences.add(a + "," + b + "," + c + "," + d);return sequences;}if (canFormArithmeticSequences(nums).size()!=0){sequences.add(a + "," + b + "," + c + "," + d);}if (flag) {nums.add(a);nums.add(b);nums.add(c);nums.add(d);}Collections.sort(nums);}}}}}return sequences;}private static boolean isArithmeticSequence(int a, int b, int c, int d) {int[] arr = {a, b, c, d};return (arr[1] - arr[0] == arr[2] - arr[1]) && (arr[2] - arr[1] == arr[3] - arr[2]);}public static void main(String[] args) {for (int m = 1; m < 6; m++){System.out.print("当数列的m值为："+m+"时：使数列成为可分数列的(i,j)为：\t");// 定义一个ArrayList来存储Int类型的数据List<Integer> numbers = new ArrayList<>();for (int i = 1; i <= 4*m+2; i++){numbers.add(Integer.valueOf(i));}int len = numbers.size();for (int j = 0; j < len; j++) {numbers.remove(j);for (int k = j+1; k < len; k++) {numbers.remove(k-1);if (canFormArithmeticSequences(numbers).size()!=0){System.out.print("("+Integer.valueOf(j+1)+","+Integer.valueOf(k+1)+")、");}numbers.add(Integer.valueOf(k+1));Collections.sort(numbers);}numbers.add(Integer.valueOf(j+1));Collections.sort(numbers);}System.out.println();}}
}

这篇关于秒解-今年高考数学压轴题，你不知道有多爽！附带：计算机程序验证结果的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！