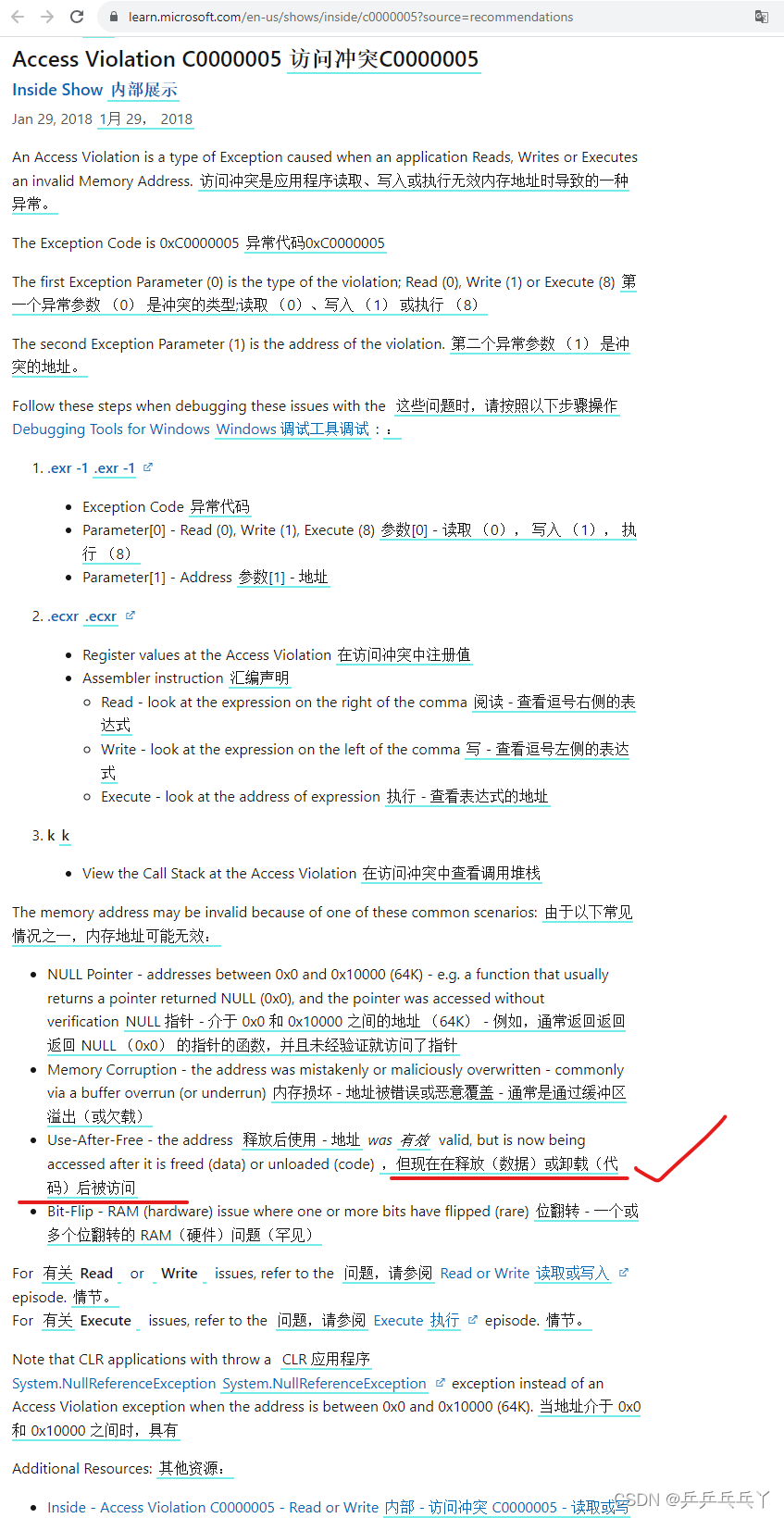
程序验证专题
秒解-今年高考数学压轴题，你不知道有多爽！附带：计算机程序验证结果
同步的公众号文章在此，今年高考数学-压轴题 原来可以秒解啊！附带：计算机程序验证结果没错，其实高考数学-压轴题其实可以秒解的呀~https://mp.weixin.qq.com/s/4M50qP9MFwJOS9OpeyxvSg 没错，其实新课标I数学-压轴题其实可以秒解的呀~ 课标I的高考压轴题的截图 解析： 其实你内心想这个数列完全可以使1、2、3、4、5、6。 1、使数列成为可
360公司2015年秋季校园招聘笔试考卷(技术类 D)部分试题程序验证和解析3
一 原题 （18）以下程序的输出是: void main(int argc, char **argv){int i;for(i = 0;i < 3;i++){switch(i){case 0:printf("%d",i);case 2:printf("%d",i);default:printf("%d",i);}}} A 000102 B 000020 C 00012
程序验证（七）：可满足性模理论(Satisfiability Modulo Theories)
程序验证（七）：可满足性模理论(Satisfiability Modulo Theories) SMT Satisfiability Modulo Theories(SMT)是以下情况的公式的判定问题： 一些一阶理论的复合具有任意的布尔结构 DPLL( T T T): DPLL Modulo Theories 这是现代SMT求解器的基础技术 将SMT问题分解为我呢吧可以高效求解的子问题：
程序验证（六）：纳尔逊-欧朋算法(Nelson-Oppen Procedure)
程序验证（六）：纳尔逊-欧朋算法(Nelson-Oppen Procedure) 动机 截至目前，我们学习了一些一阶理论，每一个都是关于某一种数据类型 然而，现实中的公式并不是由单一的理论组成，如： ∀ i . 0 ≤ i ≤ n → a [ i ] ≤ a [ i + 1 ] \forall i.0\le i\le n\to a[i]\le a[i+1] ∀i.0≤i≤n→a[i]≤a[i
程序验证（五）：一阶理论的过程
程序验证（五）：一阶理论的过程 主要讨论 T E T_E TE的量词自由片段以及 T A T_A TA 等价理论的判定 等价及未解释函数理论(Theory of Equality and Uninterpreted Functions) 除=外的谓词实际上使我们的讨论不必要地复杂化，去除这些累赘谓词的方法如下： 对每个谓词 p p p，引入一个新的(fresh)函数符号 f p f_
程序验证（十）：演绎验证（上）
程序验证（十）：演绎验证（上） 基础路径(Basic Approach) 给定一个程序 c c c，由以下specification注解： { P } c { Q } \{P\}c\{Q\} {P}c{Q} 为了证明这个三元组，我们构造一个验证条件(verification condition， VC)的集合 每个VC都是某个理论的一阶公式如果所有的VC都是永真的，那么 { P } c {
程序验证（九）：程序正确性规范
程序验证（九）：程序正确性规范 什么是程序的正确性？应当在指定的前提下，进行预定的行为，达到指定的结果。 部分正确性(Partial Correctness) 部分正确性指的是一个程序的停止行为 我们将部分正确性用霍尔三元组(Hoare triples)表达： { P } c { Q } \{P\}c\{Q\} {P}c{Q} 这里： c c c是一个程序 P P P和 Q Q Q是一
程序验证（八）：形式语义
程序验证（八）：形式语义 语义描述方法 如下： 操作语义：用抽象机描述程序执行引起的状态改变，关心状态改变是怎样产生的，与语言的实现关系紧密。指称语义：使程序执行的效果对应数学对象，只关心程序执行的效果，不关心其是怎样产生的。公理语义：将程序的语义性质表示为命题，采用数理逻辑的方法研究。 引入玩具语言Imp 语法范畴 如下： 数字集 N u m Num Num，用 n n n表示数字
![[INS-30131]执行安装程序验证所需的初始设置失败](https://img-blog.csdn.net/20180124125336723?watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvc2hpeXUxMTU3NzU4NjU1/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/SouthEast)
[INS-30131]执行安装程序验证所需的初始设置失败
问题描述，昨天在给客户安装Windows Oracle11g 的时候，遇到下面的报错信息： 尝试网上各种方法以后没有得到解决，于是在MOS 上寻找答案： 于是利用下面的方式按照即可通过： setup.exe -ignorePrereq -J"-Doracle.install.db.validate.supportedOSCheck=false"
![[INS-30131]执行安装程序验证所需的初始设置失败（无法访问临时位置）](https://img-blog.csdnimg.cn/2e7634c54d4c4528a3c7fe37ccb75bf6.png)
[INS-30131]执行安装程序验证所需的初始设置失败（无法访问临时位置）
前言 作为一个Oracle DBA 经常部署window Oracle，尤其是Oracle11G（11.2.0.4.0），难免就会遇到这样的情况，安装时，在执行检查环境步骤时候报错：[INS-30131]执行安装程序验证所需的初始设置失败（无法访问临时位置），下面就来讲下如何处理。 一、解决方法 报错截图 1.部署Oracle11g服务端时报错INS-30131处理
调试工具：应用程序验证器Application Verifier（配合WinDbg）
1.应用程序验证器（Application Verifier）简介 说明：Application Verifier是来自微软官方的一款应用程序验证工具，主要用于帮助用户检测和调试内存损坏、危险的安全漏洞、Run-time检测等；是一款辅助开发工具，不用修改源码；在程序退出时报告未释放的资源等，程序正常退出才会有报告 获取：可以通过windows software development Kit
调试工具：应用程序验证器Application Verifier（配合WinDbg）
1.应用程序验证器（Application Verifier）简介 说明：Application Verifier是来自微软官方的一款应用程序验证工具，主要用于帮助用户检测和调试内存损坏、危险的安全漏洞、Run-time检测等；是一款辅助开发工具，不用修改源码；在程序退出时报告未释放的资源等，程序正常退出才会有报告 获取：可以通过windows software development Kit
oracle安装报错设置注册,安装oracle11g INS-30131执行安装程序验证所需的初始设置失败的解决方法...
安装oracle11g [INS-30131] 执行安装程序验证所需的初始设置失败。 @H_404_6@ 第一步： @H_404_6@控制面板>所有控制面板项>管理工具>服务>SERVER 启动 TCP/IP 启动 第二步：@H_404_6@ 1.点击 开始->运行 ，输入regedit,然后回车键进入注册编辑器 2.找到并点击HKEY_LOCAL_MACHINE\SYSTEM\Curren