本文主要是介绍快排(快速排序)的递归与非递归实现(文末附完整代码),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
快排有几种不同的写法,下面一一来介绍并实现。其中又分为递归和非递归的写法,但大体思路相同,只是代码实现略有不同。(注:文章中的完整代码中,Swap()函数均省略未写,记得自己补充)
递归写法
递归的写法类似于二叉树的前序遍历,先数组本身排序,再递归左右两个区间,直至将无序数组变为有序。
hoare版本
霍尔版本是快排的提出者,也就是最开始的写法。
其基于分治的思想,在数组中选中一个值作为基准(keyi),利用这个值(a[keyi]),进行排序,将待排序元素分为两份,比a[keyi]小的值在其左侧,比a[keyi]大的值在其右侧。此时a[keyi]这个值就排好序了,然后用递归的方法对左右两侧进行重复操作,直至无序数组变为有序。
一次排序过程如下:
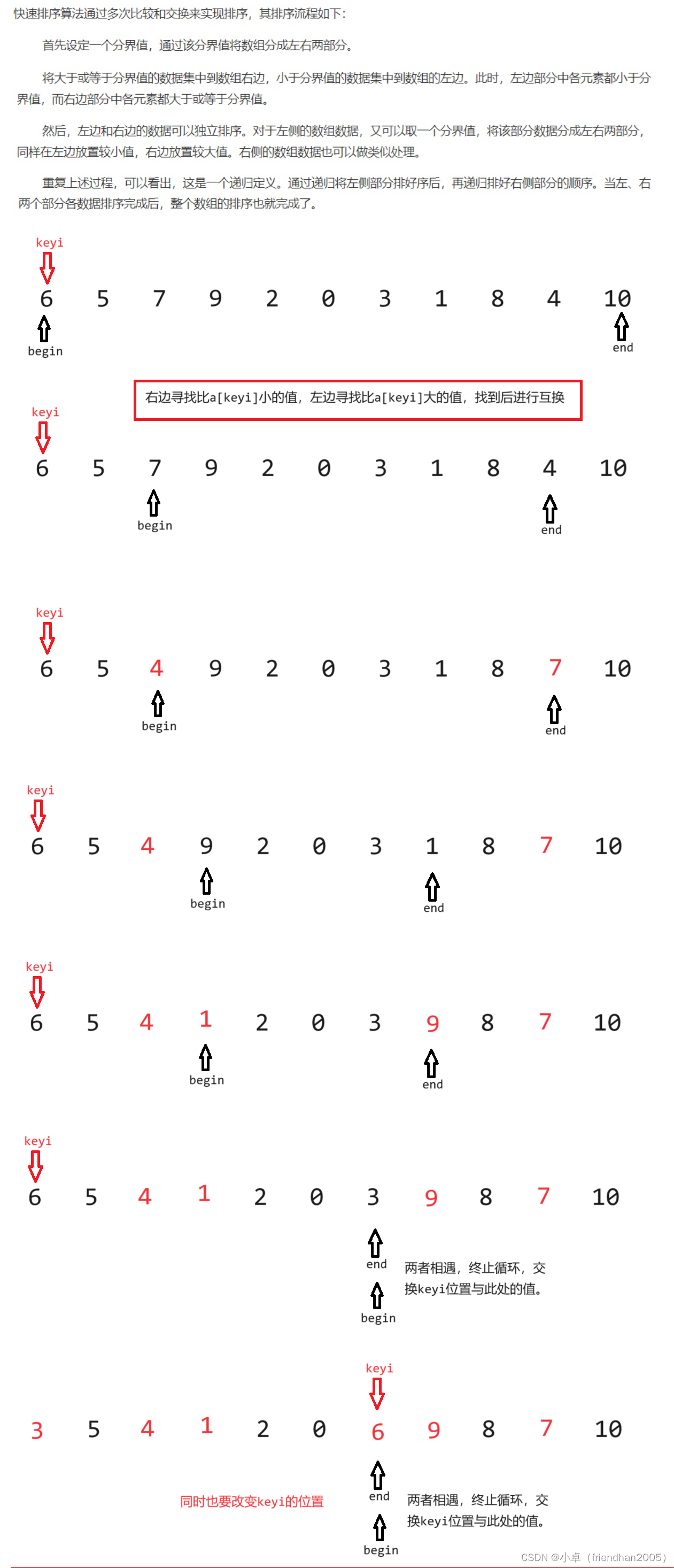
其中,还有一些小问题需要注意:



代码实现为:
// 快速排序hoare版本
int PartSort(int* a, int left, int right)
{int keyi = left;int begin = left, end = right;while (begin < end){//右边找小while (begin < end && a[end] >= a[keyi]){end--;}//左边找大while (begin < end && a[begin] <= a[keyi]){begin++;}Swap(&a[begin], &a[end]);}Swap(&a[keyi], &a[begin]);keyi = begin;return keyi;
}void QuickSort(int* a, int left, int right)
{if (left >= right){return;}int keyi = PartSort(a, left, right);QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);
}挖坑法
挖坑法的思想是选中一个坑位(其值记为tmp,坑位的起始位置为begin),然后从右边找比tmp小的值,填入其中(此时要begin++),然后从左边找比tmp大的值填入新的坑位(此时坑位在end处,填入后要end--)。
最后begin和end相遇时,将tmp的值填入。
代码实现为:
// 挖坑法
int PartSort(int* a, int left, int right)
{int tmp = a[left];int begin = left, end = right;while (begin < end){while (begin < end && a[end] >= tmp){end--;}a[begin] = a[end];if (begin >= end){break;}begin++;while (begin < end && a[begin] <= tmp){begin++;}a[end] = a[begin];if (begin >= end){break;}end--;}a[begin] = tmp;return begin;
}void QuickSort(int* a, int left, int right)
{if (left >= right){return;}int keyi = PartSort(a, left, right);QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);
}写的这个版本看起来有些长,原因是我在写时,没有再用一个变量来记录坑位的位置,我们可以再添加一个变量来记录坑位的位置。
// 挖坑法
int PartSort(int* a, int left, int right)
{int tmp = a[left];int begin = left, end = right;int key = begin;while (begin < end){while (begin < end && a[end] >= tmp){end--;}a[key] = a[end];key = end;while (begin < end && a[begin] <= tmp){begin++;}a[key] = a[begin];key = begin;}a[key] = tmp;return key;
}void QuickSort(int* a, int left, int right)
{if (left >= right){return;}int keyi = PartSort(a, left, right);QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);
}一趟排序过程如下:

双指针
双指针法的中心思想是利用 prev 和 cur 两个指针来操作。
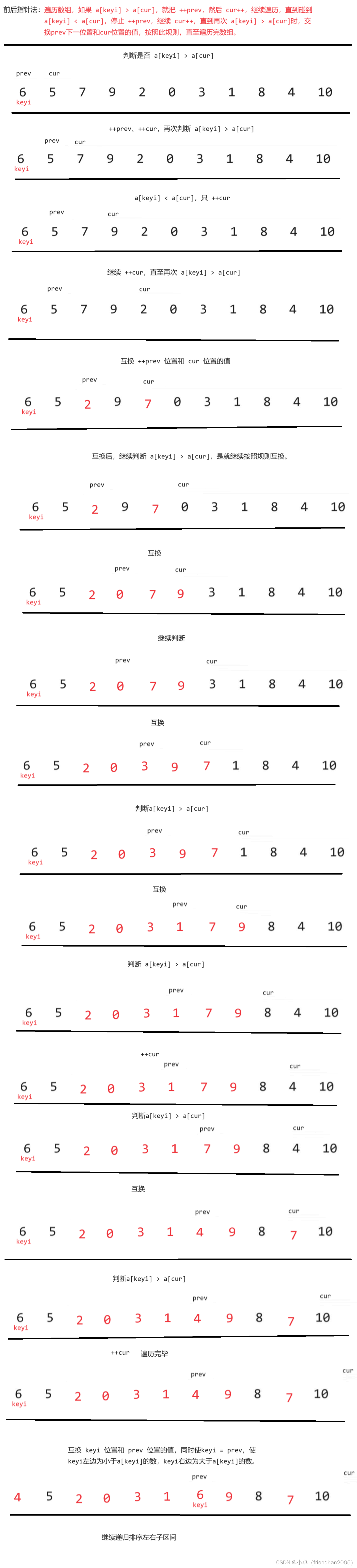
具体代码实现如下:
// 快速排序前后指针法
int PartSort3(int* a, int left, int right)
{int keyi = left;int prev = left, cur = left + 1;while (cur <= right){//这里如果a[keyi] > a[cur],就会判断++prev != cur,//prev就会加一,只有prev和cur所在位置不同时才会发生交换。if (a[keyi] > a[cur] && ++prev != cur){Swap(&a[prev], &a[cur]);}cur++;}//最后交换prev位置和keyi位置的值Swap(&a[prev], &a[keyi]);keyi = prev;return keyi;
}void QuickSort(int* a, int left, int right)
{if (left >= right){return;}int keyi = PartSort3(a, left, right);QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);
}非递归
有时候,递归深度太深会导致栈溢出,所以我们有时要用非递归来实现快排,非递归实现快排,我们就需要借助栈来实现。其思想就是模拟递归的过程,并用循环来替代,循环每走一次,就相当于递归了一次。所以要用栈来记录每次要排序的区间(也就是每次递归的 left 和 right )。栈的实现详解(点这里)。
// 快速排序hoare版本
int PartSort(int* a, int left, int right)
{int keyi = left;int begin = left, end = right;while (begin < end){//右边找小while (begin < end && a[end] >= a[keyi]){end--;}//左边找大while (begin < end && a[begin] <= a[keyi]){begin++;}Swap(&a[begin], &a[end]);}Swap(&a[keyi], &a[begin]);keyi = begin;return keyi;
}#include "Stacktest.h"// 快速排序 非递归实现
void QuickSortNonR(int* a, int left, int right)
{stack st;StackInit(&st);//先入右,再入左StackPush(&st, right);StackPush(&st, left);while (!StackEmpty(&st)){int begin = StackTop(&st);StackPop(&st);int end = StackTop(&st);StackPop(&st);//排序int keyi = PartSort(a, begin, end);if (keyi + 1 < end){StackPush(&st, end);StackPush(&st, keyi + 1);}if (begin < keyi - 1){StackPush(&st, keyi - 1);StackPush(&st, begin);}}StackDestory(&st);
}具体过程如下:

优化
快排中 keyi 的选取是十分最重要的,快排的时间复杂度为O(N*logN),但其最坏情况下为O(N^2),如果基准值是数组中最大或最小的数值,则快速排序的递归深度会非常深,排序效率会很低。若是一个有序数组使用快速排序,则递归深度为n,单趟排序也为n,此时时间复杂度为O(N^2),为了避免最坏情况的发生,我们通常是在数组中随意选择一个数作为基准。这里有几种方法:随机数法、取中间位置和三数取中法。
随机数法
随机选一个,有概率选到最大值或最小值。
#include<stdlib.h>
#include<time.h>int GetNumber(int* a, int left, int right)
{return rand() % (right - left + 1) + left;
}// 快速排序hoare版本
int PartSort1(int* a, int left, int right)
{int n = GetNumber(a, left, right);Swap(&a[left], &a[n]);int keyi = left;int begin = left, end = right;while (begin < end){//右边找小while (begin < end && a[end] >= a[keyi]){end--;}//左边找大while (begin < end && a[begin] <= a[keyi]){begin++;}Swap(&a[begin], &a[end]);}Swap(&a[keyi], &a[begin]);keyi = begin;return keyi;
}void QuickSort(int* a, int left, int right)
{if (left >= right){return;}int keyi = PartSort1(a, left, right);QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);
}int main()
{srand((unsigned int)time(NULL));int arr[] = { 6,5,7,9,2,0,3,1,8,4,10 };int len = sizeof(arr) / sizeof(int);QuickSort(arr, 0, len - 1);//打印数组Print(arr, len);return 0;
}取中间位置的数
取中间元素位置,也有可能选到最大值或最小值。
#include<stdlib.h>
#include<time.h>int GetNumber(int* a, int left, int right)
{return (right + left) / 2;
}// 快速排序hoare版本
int PartSort1(int* a, int left, int right)
{int n = GetNumber(a, left, right);Swap(&a[left], &a[n]);int keyi = left;int begin = left, end = right;while (begin < end){//右边找小while (begin < end && a[end] >= a[keyi]){end--;}//左边找大while (begin < end && a[begin] <= a[keyi]){begin++;}Swap(&a[begin], &a[end]);}Swap(&a[keyi], &a[begin]);keyi = begin;return keyi;
}void QuickSort(int* a, int left, int right)
{if (left >= right){return;}int keyi = PartSort1(a, left, right);QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);
}int main()
{srand((unsigned int)time(NULL));int arr[] = { 6,5,7,9,2,0,3,1,8,4,10 };int len = sizeof(arr) / sizeof(int);QuickSort(arr, 0, len - 1);//打印数组Print(arr, len);return 0;
}三数取中法
三数取中法是指比较最左边、最右边和中间元素的大小选出折中值。不会选到最大值或最小值。
#include<stdlib.h>
#include<time.h>int GetNumber(int* a, int left, int right)
{int mid = (right + left) / 2;if (a[left] < a[mid]){if (a[mid] < a[right]){return mid;}else if (a[left] < a[right]){return right;}else{return left;}}else //a[mid] <= a[left]{if (a[mid] > a[right]){return mid;}else if (a[left] < a[right]){return left;}else{return right;}}
}// 快速排序hoare版本
int PartSort1(int* a, int left, int right)
{int n = GetNumber(a, left, right);Swap(&a[left], &a[n]);int keyi = left;int begin = left, end = right;while (begin < end){//右边找小while (begin < end && a[end] >= a[keyi]){end--;}//左边找大while (begin < end && a[begin] <= a[keyi]){begin++;}Swap(&a[begin], &a[end]);}Swap(&a[keyi], &a[begin]);keyi = begin;return keyi;
}void QuickSort(int* a, int left, int right)
{if (left >= right){return;}int keyi = PartSort1(a, left, right);QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);
}小区间优化
递归不断的拆分左右区间,越往深递归,所耗费的时间就越多,当递归至区间中元素个数为个位数字时,使用快排反而降低了效率,这是我们可以考虑使用插入排序来进行小区间优化。
void QuickSort(int* a, int left, int right)
{if (left >= right){return;}//小区间优化if ((right - left + 1) < 10){InsertSort(a + left, left, right);}else{int keyi = PartSort1(a, left, right);QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);}
}完整代码
#include<stdio.h>
#include<stdlib.h>
#include<time.h>void Swap(int* p1, int* p2)
{int* tmp = *p1;*p1 = *p2;*p2 = tmp;
}void Print(int* arr, int n)
{for (int i = 0; i < n; i++){printf("%d ", arr[i]);}printf("\n");
}//插入排序
void InsertSort(int* a, int n)
{for (int i = 1; i < n - 1; i++){int end = i;int tmp = a[end + 1];while (end >= 0){if (tmp < a[end]){a[end + 1] = a[end];end--;}else{break;}}a[end + 1] = tmp;}
}// 快速排序递归实现int GetNumber(int* a, int left, int right)
{//return (right - left) / 2;//return rand() % (right - left + 1) + left;int mid = (right + left) / 2;if (a[left] < a[mid]){if (a[mid] < a[right]){return mid;}else if (a[left] < a[right]){return right;}else{return left;}}else //a[mid] <= a[left]{if (a[mid] > a[right]){return mid;}else if (a[left] < a[right]){return left;}else{return right;}}
}// 快速排序hoare版本
int PartSort1(int* a, int left, int right)
{int n = GetNumber(a, left, right);Swap(&a[left], &a[n]);int keyi = left;int begin = left, end = right;while (begin < end){//右边找小while (begin < end && a[end] >= a[keyi]){end--;}//左边找大while (begin < end && a[begin] <= a[keyi]){begin++;}Swap(&a[begin], &a[end]);}Swap(&a[keyi], &a[begin]);keyi = begin;return keyi;
}// 快速排序挖坑法
int PartSort2(int* a, int left, int right)
{int tmp = a[left];int begin = left, end = right;int key = begin;while (begin < end){while (begin < end && a[end] >= tmp){end--;}/*a[begin] = a[end];if (begin >= end){break;}begin++;*/a[key] = a[end];key = end;while (begin < end && a[begin] <= tmp){begin++;}/*a[end] = a[begin];if (begin >= end){break;}end--;*/a[key] = a[begin];key = begin;}a[key] = tmp;return key;
}// 快速排序前后指针法
int PartSort3(int* a, int left, int right)
{int keyi = left;int prev = left, cur = left + 1;while (cur <= right){//这里如果a[keyi] > a[cur],就会判断++prev != cur,//prev就会加一,只有prev和cur所在位置不同时才会发生交换。if (a[keyi] > a[cur] && ++prev != cur){Swap(&a[prev], &a[cur]);}cur++;}//最后交换prev位置和keyi位置的值Swap(&a[prev], &a[keyi]);keyi = prev;return keyi;
}void QuickSort(int* a, int left, int right)
{if (left >= right){return;}//小区间优化if ((right - left + 1) < 10){InsertSort(a + left, left, right);}else{int keyi = PartSort1(a, left, right);QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);}
}#include "Stacktest.h"// 快速排序 非递归实现
void QuickSortNonR(int* a, int left, int right)
{stack st;StackInit(&st);StackPush(&st, right);StackPush(&st, left);while (!StackEmpty(&st)){int begin = StackTop(&st);StackPop(&st);int end = StackTop(&st);StackPop(&st);int keyi = PartSort1(a, begin, end);if (keyi + 1 < end){StackPush(&st, end);StackPush(&st, keyi + 1);}if (begin < keyi - 1){StackPush(&st, keyi - 1);StackPush(&st, begin);}}StackDestory(&st);
}int main()
{srand((unsigned int)time(NULL));int arr[] = { 6,5,7,9,2,0,3,1,8,4,10 };int len = sizeof(arr) / sizeof(int);QuickSort(arr, 0, len - 1);Print(arr, len);return 0;
}这篇关于快排(快速排序)的递归与非递归实现(文末附完整代码)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






