本文主要是介绍【传知代码】基于曲率的图重新布线（论文复现），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
前言：在图形处理中，一个至关重要的问题是图形的重新布线，即在不改变图形基本结构的前提下，通过调整节点间的连接关系，使图形具有更好的性质，如更低的复杂度、更高的可视化效果或更强的鲁棒性。传统的图形重新布线方法往往依赖于直观的经验或简单的启发式算法，难以适应复杂多变的应用场景，近年来，基于曲率的图重新布线技术应运而生，为图形优化领域带来了新的曙光。与传统的方法相比，基于曲率的图重新布线技术更加注重图形局部的几何特性，通过计算节点的曲率来指导重新布线的过程。
本文所涉及所有资源均在传知代码平台可获取
目录
概述
演示效果
核心代码
写在最后
概述
大部分的图神经网络（Graph Neural Networks GNN）采用消息传递模式，在这种模式下，节点的特性会在输入的图上进行传递。近期的科学研究揭示，来自遥远节点的信息丢失确实是影响依赖于远程交互任务的消息传输效率的一个关键因素。这种限制通常被命名为“过度挤压”（Over-squashing）。图中每个结点的k跳邻居数量会随着k的增加而指数级增加，这导致远距离结点的信息很难被压缩到固定大小的结点特征中，从而造成信息的丢失，这是过度挤压的原因，这里参考了一下这篇论文，地址 具体如下：
这篇文章为我们提供了GNN中的过度挤压现象的详细描述，并探讨了它是如何从图表中的瓶颈问题中产生的。因此，本研究提出了一种创新的基于边的组合曲率方法，并成功证实了负曲率边是引发过度挤压问题的根本原因。此外，本文还介绍了一种利用曲率进行图重现布线的策略，旨在减轻过度挤压的问题，如下图所示，上图：曲面上曲率的演变可能会减少瓶颈。下图：本文展示了如何在图上做同样的事情来提高GNN的性能。蓝色代表负曲率；红色代表正曲率：
接下来对本次论文讲述的核心算法进行如下一个简单的讲解：
1）黎曼几何中的一个自然对象是里奇曲率（Ricci curvature），这是一种决定测地线色散的双线性形式，即从“相同”速度的附近点开始的测地线是否保持平行（欧几里得空间）、收敛（球面空间）或发散（双曲空间）。
2）算法在每次迭代中都会添加一条边来支持图中最负曲率的边，然后移除最正曲率的边。
3）要求k∈B1(i),l∈B1(j)k∈B1(i),l∈B1(j)是为了确保我们在最负曲率的边i∼ji∼j周围添加额外的3-cycle或4-cycle。这是一个局部修改。
4）原始输入图和重新布线图之间的图编辑距离以max number of iterations的2倍为界。
5）temperatureτ>0τ>0决定了添加边的随机程度，τ=∞τ=∞表示总是添加最佳边。
6）移除曲率最大的边是为了平衡曲率和结点的度的分布。
7）使用Balanced Forman curvature计算Ric(i,j)Ric(i,j)
8）optimal Ric upper-boundC+C+用于防止算法使得曲率分布负偏斜。C+=∞C+=∞表示不移除任何边。
如下图所示：
演示效果
本次代码支持Cora, Citeseer, Pubmed, Cornell, Texas, Wisconsin 脚本自动下载，如不能请参考geom-gcn ，这里不同数据集的配置文件位于./configs/。运行之前需要修改数据集根目录和输出目录：
output_dir: $OUTPUT_DIR$
data:root: $DATA_ROOT$测试集和训练集可以采用下面的方式进行：
# train on train data splits
python train.py --config-file configs/*.yaml
# test on val and test data splits
python eval.py --config-file configs/*.yaml
// 或
search_dir=configs
for file in "$search_dir"/*
dopython train.py --config-file $filepython eval.py --config-file $file
done运行结果可以参考下面的方式，运行日志、模型权重、重新布线结果保存在$OUTPUT_DIR/$DATASET_NAME/ 测试结果（accuracy）保存在./result.csv：
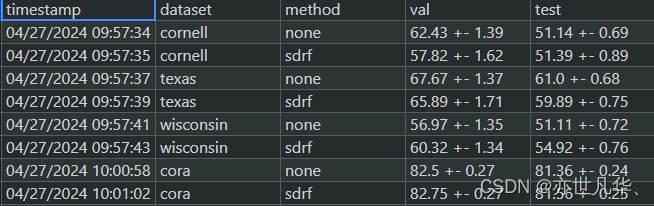
核心代码
下面这段代码实现了对图数据进行流形学习的过程，其中使用了 Ricci 曲率作为度量距离的方法。具体来说，代码实现了一个基于 Ricci 曲率的图形变形算法，即 SDRF（Spectral Deformation and Ricci Flow）算法，该算法主要包含以下步骤：
1）将 Pytorch Geometric 中的数据类型 Data 转换为 NetworkX 中的数据类型 DiGraph，方便后续的加边、减边操作。
2）获取图的邻接矩阵和边的个数。
3）进入图的加边、减边循环过程，其中 max_iterations 为最大迭代次数：
4）将 NetworkX 中的数据类型 DiGraph 转换为 Pytorch Geometric 中的数据类型 Data，并返回。
其中，BFC 算法是一种计算曲率的方法，用于计算 Ricci 曲率矩阵。具体来说，它通过计算形式曲率和平衡形式曲率之间的差异来计算 Ricci 曲率。在算法中，balanced_forman_curvature 函数用于计算 Ricci 曲率矩阵，balanced_forman_post_delta 函数用于计算边添加之后对 Ricci 曲率的提升程度。
SDRF 算法是一种流形学习算法，用于在图数据中计算距离和相似度。通过迭代加边、减边的方法，SDRF 算法可以将图数据进行形变，从而使得距离和相似度更加符合实际情况，代码如下：
def sdrf(data, max_iterations=10, remove_edges=True, remove_bound=0.5, tau=1.0, undirected=True):# 1. 将torch_geometric.data.Data实例转化为networkx.DiGraph实例，方便后续加边、减边操作G = to_networkx(data)if undirected:G = G.to_undirected()# 2. 获取图信息（邻接矩阵，边的个数）edge_index = data.edge_indexif undirected:edge_index = to_undirected(edge_index)A = to_dense_adj(remove_self_loops(edge_index)[0])[0] # 邻接矩阵A = A.cuda()N = A.shape[0] # 边的个数C = torch.zeros(N, N).cuda() # 初始化Ricci曲率矩阵，即Ric(i, j)# 3. 进入图的加边、减边循环过程，其中max_iterations为最大迭代次数for x in range(max_iterations):can_add = True# 3.1 根据BFC算法更新Ricci曲率矩阵balanced_forman_curvature(A, C=C)ix_min = C.argmin().item()x = ix_min // Ny = ix_min % N# 3.2 计算可加边的候选集candidatesif undirected:x_neighbors = list(G.neighbors(x)) + [x]y_neighbors = list(G.neighbors(y)) + [y]else:x_neighbors = list(G.successors(x)) + [x]y_neighbors = list(G.predecessors(y)) + [y]candidates = []for i in x_neighbors:for j in y_neighbors:if (i != j) and (not G.has_edge(i, j)):candidates.append((i, j))# 3.3 根据边添加之后对Ricci曲率的提升程度，从候选集中选择边k~l进行添加if len(candidates):D = balanced_forman_post_delta(A, x, y, x_neighbors, y_neighbors)improvements = []for i, j in candidates:improvements.append((D - C[x, y])[x_neighbors.index(i), y_neighbors.index(j)].item())k, l = candidates[np.random.choice(range(len(candidates)), p=softmax(np.array(improvements), tau=tau))]G.add_edge(k, l) # 添加边if undirected:A[k, l] = A[l, k] = 1else:A[k, l] = 1else:can_add = Falseif not remove_edges:break# 3.4 移除具有最大Ricci曲率的边，其中remove_bound为曲率最大上界if remove_edges:ix_max = C.argmax().item()x = ix_max // Ny = ix_max % Nif C[x, y] > remove_bound:G.remove_edge(x, y) # 移除边if undirected:A[x, y] = A[y, x] = 0else:A[x, y] = 0else:if can_add is False:break# 4. 将networkx.DiGraph实例转化为torch_geometric.data.Data实例，返回return from_networkx(G)写在最后
在探索图形优化技术的道路上，基于曲率的图重新布线技术以其独特的视角和强大的能力，为我们揭示了图形处理领域的新可能。通过对节点曲率的精确计算和合理利用，这一技术不仅能够保持图形的整体结构稳定，更能在细节上精雕细琢，使图形展现出更加平滑、美观的视觉效果。
回顾我们所探讨的内容，基于曲率的图重新布线技术凭借其先进性和实用性，已经在多个领域展现出了巨大的应用潜力。无论是社交网络分析中的用户关系优化，还是城市规划中的道路网络设计，甚至是生物科学中的蛋白质交互图研究，这一技术都为我们提供了全新的解决方案，随着技术的不断进步和应用领域的不断拓展，基于曲率的图重新布线技术将会迎来更加广阔的发展空间。我们可以预见，未来的图形优化将更加注重局部细节的优化和整体结构的稳定性，而基于曲率的图重新布线技术正是这一趋势的引领者。
详细复现过程的项目源码、数据和预训练好的模型可从该文章下方附件获取。
这篇关于【传知代码】基于曲率的图重新布线（论文复现）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
