【基础算法】(04) 十二种排序算法（第四篇）

本文主要是介绍【基础算法】(04) 十二种排序算法（第四篇），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

【基础算法】(04) 十二种排序算法（第四篇）

Auther: Thomas Shen
E-mail: Thomas.shen3904@qq.com
Date: 2017/10/21
All Copyrights reserved !

---

1. 篇述：

本系列总结了常用的十二种排序算法，每个算法都包括算法原理, 代码实现, 面试例题 三部分。

其中本文是排序算法系列的第三篇，介绍了：

• 11. 桶排序 (Bucket sort),
• 12. 计数排序 (Counting sort),
• 13. 基数排序 (Radix Sort),

---

2. 直接插入排序 (Straight Insertion Sort)：

3. 二分插入排序 （Binary insert sort)：

4. 希尔排序 （Shell’s Sort）：

5. 选择排序—简单选择排序（Simple Selection Sort）：

6. 选择排序—堆排序（Heap Sort）：

7. 交换排序—冒泡排序（Bubble Sort）：

8. 鸡尾酒排序/双向冒泡排序：

9. 交换排序—快速排序（Quick Sort）：

10. 归并排序（Merge Sort）：

参见第一、二、三篇；

---

11. 桶排序 (Bucket sort)：

桶排序 (Bucket sort)或所谓的箱排序，是一个排序算法，工作的原理是将数组分到有限数量的桶子里。每个桶子再个别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序）。

桶排序是稳定的，且在大多数情况下常见排序里最快的一种,比快排还要快，缺点是非常耗空间,基本上是最耗空间的一种排序算法，而且只能在某些情形下使用。

11.1 原理简介：
桶排序具体算法描述如下：

1. 设置一个定量的数组当作空桶子。
2. 寻访串行，并且把项目一个一个放到对应的桶子去。
3. 对每个不是空的桶子进行排序。
4. 从不是空的桶子里把项目再放回原来的串行中。

桶排序最好情况下使用线性时间O(n)，很显然桶排序的时间复杂度，取决与对各个桶之间数据进行排序的时间复杂度，因为 其它部分的时间复杂度都为O(n);很显然，桶划分的越小，各个桶之间的数据越少，排 序所用的时间也会越少。但相应的空间消耗就会增大。

可以证明，即使选用插入排序作为桶内排序的方法，桶排序的平均时间复杂度为线性。 具体证明，请参考算法导论。其空间复杂度也为线性。

桶排序是一种很巧妙的排序方法，在处理密集型数排序的时候有比较好的效果(主要是这种情况下空间复杂度不高)

11.2 代码实现：

#include <time.h>  
#include <iostream>  
#include <iomanip>  
using namespace  std;  /*initial arr*/  
void InitialArr(double *arr,int n)  
{  srand((unsigned)time(NULL));  for (int i = 0; i<n;i++)  {  arr[i] = rand()/double(RAND_MAX+1);   //(0.1)  }  
}  /* print arr*/  
void PrintArr(double *arr,int n)  
{  for (int i = 0;i < n; i++)  {  cout<<setw(15)<<arr[i];  if ((i+1)%5 == 0 || i ==  n-1)  {  cout<<endl;  }  }  
}  void BucketSort(double * arr,int n)       
{  double **bucket = new double*[10];  for (int i = 0;i<10;i++)  {  bucket[i] = new double[n];  }  int count[10] = {0};  for (int i = 0 ; i < n ; i++)  {  double temp = arr[i];  int flag = (int)(arr[i]*10); //flag标识小树的第一位   bucket[flag][count[flag]] = temp; //用二维数组的每个向量来存放小树第一位相同的数据  int j = count[flag]++;  /* 利用插入排序对每一行进行排序 */  for(;j > 0 && temp < bucket[flag][j - 1]; --j)  {  bucket[flag][j] = bucket[flag][j-1];  }  bucket[flag][j] =temp;  }  /* 所有数据重新链接 */  int k=0;  for (int i = 0 ; i < 10 ; i++)  {  for (int j = 0 ; j< count[i];j++)  {  arr[k] = bucket[i][j];  k++;  }  }  for (int i = 0 ; i<10 ;i++)  {  delete bucket[i];  bucket[i] =NULL;  }  delete []bucket;  bucket = NULL;  
}  void main()  
{  double *arr=new double[10];  InitialArr(arr, 10);  BucketSort(arr, 10);  PrintArr(arr,10);  delete [] arr;  
}  

11.3 面试例题：
11.3.1 例题一：

一年的全国高考考生人数为500 万，分数使用标准分，最低100 ，最高900 ，没有小数，你把这500 万元素的数组排个序。

对500W数据排序，如果基于比较的先进排序，平均比较次数为O(5000000*log5000000)≈1.112亿。但是我们发现，这些数据都有特殊的条件： 100 =< score <= 900。那么我们就可以考虑桶排序这样一个“投机取巧”的办法、让其在毫秒级别就完成500万排序。

创建801(900-100)个桶。将每个考生的分数丢进f(score)=score-100的桶中。这个过程从头到尾遍历一遍数据只需要500W次。然后根据桶号大小依次将桶中数值输出，即可以得到一个有序的序列。而且可以很容易的得到100分有xxx人，501分有xxx人。

实际上，桶排序对数据的条件有特殊要求，如果上面的分数不是从100-900，而是从0-2亿，那么分配2亿个桶显然是不可能的。所以桶排序有其局限性，适合元素值集合并不大的情况。

11.3.2 例题二：
在一个文件中有 10G 个整数，乱序排列，要求找出中位数。内存限制为 2G。只写出思路即可（内存限制为 2G的意思就是，可以使用2G的空间来运行程序，而不考虑这台机器上的其他软件的占用内存）。

分析： 既然要找中位数，很简单就是排序的想法。那么基于字节的桶排序是一个可行的方法。

按以下步骤实施：

1. 把10G整数每2G读入一次内存，然后一次遍历这536,870,912即（1024*1024*1024）*2 /4个数据。每个数据用位运算”>>”取出最高8位(31-24)。这8bits(0-255)最多表示255个桶，那么可以根据8bit的值来确定丢入第几个桶。最后把每个桶写入一个磁盘文件中，同时在内存中统计每个桶内数据的数量，自然这个数量只需要255个整形空间即可。
2. 继续以内存中的整数的次高8bit进行桶排序(23-16)。过程和第一步相同，也是255个桶。
3. 一直下去，直到最低字节(7-0bit)的桶排序结束。我相信这个时候完全可以在内存中使用一次快排就可以了。

11.3.3 例题三：
给定n个实数x1,x2,…,xn,求这n个实数在实轴上相邻2个数之间的最大差值M,要求设计线性的时间算法
典型的最大间隙问题。

要求线性时间算法。需要使用桶排序。桶排序的平均时间复发度是O(N).如果桶排序的数据分布不均匀，假设都分配到同一个桶中，最坏情况下的时间复杂度将变为O(N^2).

桶排序: 最关键的建桶，如果桶设计得不好的话桶排序是几乎没有作用的。通常情况下，上下界有两种取法，第一种是取一个10^n或者是2^n的数，方便实现。另一种是取数列的最大值和最小值然后均分作桶。

对于这个题，最关键的一步是：由抽屉原理知：最大差值M>= (Max(V[n])-Min(V[n]))/(n-1)！所以，假如以(Max(V[n])-Min(V[n]))/(n-1)为桶宽的话，答案一定不是属于同一个桶的两元素之差。因此，这样建桶，每次只保留桶里面的最大值和最小值即可。

代码如下：

//距离平均值为offset = (arrayMax - arrayMin) / (n - 1), 则距离最大的数必然大于这个值  
//每个桶只要记住桶中的最大值和最小值，依次比较上一个桶的最大值与下一个桶的最小值的差值，找最大的即可.  
#include <iostream>  
#define MAXSIZE 100    //实数的个数  
#define MAXNUM 32767  
using namespace std;  
struct Barrel  
{  double min;   //桶中最小的数  double max;   //桶中最大的数  bool flag;   //标记桶中有数  
};  
int BarrelOperation(double* array, int n)  
{  Barrel barrel[MAXSIZE];  //实际使用的桶  int nBarrel = 0;  //实际使用桶的个数  Barrel tmp[MAXSIZE];   //临时桶，用于暂存数据  double arrayMax = -MAXNUM, arrayMin = MAXNUM;  for(int i = 0; i < n; i++) {  if(array[i] > arrayMax)  arrayMax = array[i];  if(array[i] < arrayMin)  arrayMin = array[i];  }  double offset = (arrayMax - arrayMin) / (n - 1);  //所有数的平均间隔  //对桶进行初始化  for(i = 0; i < n; i++) {    tmp[i].flag = false;  tmp[i].max = arrayMin;  tmp[i].min = arrayMax;  }  //对数据进行分桶  for(i = 0; i < n; i++) {     int pos = (int)((array[i] - arrayMin) / offset);  if(!tmp[pos].flag) {  tmp[pos].max = tmp[pos].min = array[i];  tmp[pos].flag = true;  } else {  if(array[i] > tmp[pos].max)  tmp[pos].max = array[i];  if(array[i] < tmp[pos].min)  tmp[pos].min = array[i];  }   }  for(i = 0; i <= n; i++) {  if(tmp[i].flag)   barrel[nBarrel++] = tmp[i];     }  int maxOffset = 0.0;  for(i = 0; i < nBarrel - 1; i++) {  if((barrel[i+1].min - barrel[i].max) > maxOffset)   maxOffset = barrel[i+1].min - barrel[i].max;  }  return maxOffset;  
}  
int main()  
{  double array[MAXSIZE] = {1, 8, 6, 11, 7, 13, 16, 5};  //所需处理的数据  int n = 8; //数的个数  //double array[MAXSIZE] = {8, 6, 11};  //int n = 3;  int maxOffset = BarrelOperation(array, n);  cout << maxOffset << endl;  return 0;  
}  

---

12. 计数排序 (Counting sort)：

12.1 原理简介：
计数排序(Counting sort)是一种稳定的排序算法。计数排序使用一个额外的数组C，其中第i个元素是待排序数组A中值等于i的元素的个数。然后根据数组C来将A中的元素排到正确的位置。它只能对整数进行排序。

算法的步骤如下：
1. 找出待排序的数组中最大和最小的元素;
2. 统计数组中每个值为i的元素出现的次数，存入数组C的第i项;
3. 对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）;
4. 反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1。

当输入的元素是n 个0到k之间的整数时，它的运行时间是 O(n + k)。
计数排序不是比较排序，排序的速度快于任何比较排序算法。

由于用来计数的数组C的长度取决于待排序数组中数据的范围（等于待排序数组的最大值与最小值的差加上1），这使得计数排序对于数据范围很大的数组，需要大量时间和内存。例如：计数排序是用来排序0到100之间的数字的最好的算法，但是它不适合按字母顺序排序人名。但是，计数排序可以用在基数排序中的算法来排序数据范围很大的数组。

12.2 代码实现：

#include <stdlib.h>  
#include <string.h>  
#include <stdio.h>  
/************************************************************** 功能：计数排序。 参数： data ： 要排序的数组 size ：数组元素的个数 k   ：数组中元素数组最大值 +1 （这个需要+1） 返回值： 成功0；失败-1.        *************************************************************/  
int ctsort(int *data, int size, int k)  
{  int * counts = NULL,/*计数数组*/  * temp = NULL;/*保存排序后的数组*/  int i = 0;  /*申请数组空间*/  if ((counts = (int *) malloc( k * sizeof(int))) == NULL)  return -1;  if ((temp = (int *) malloc( k * sizeof(int))) == NULL)  return -1;  /*初始化计数数组*/  for (i = 0; i < k; i ++)  counts[i] = 0;  /*数组中出现的元素，及出现次数记录*/  for(i = 0; i < size; i++)  counts[data[i]] += 1;  /*调整元素计数中，加上前一个数*/  for (i = 1; i < k; i++)  counts[i] += counts[i - 1];  /*使用计数数组中的记录数值，来进行排序，排序后保存的temp*/  for (i = size -1; i >= 0; i --){  temp[counts[data[i]] - 1] = data[i];  counts[data[i]] -= 1;  }  memcpy(data,temp,size * sizeof(int));  free(counts);  free(temp);  return 0;  
}  
int main()  
{  int a[8] = {2,0,2,1,4,6,7,4};  int max = a[0],  i = 0;  /*获得数组中中的数值*/  for ( i = 1; i < 8; i++){  if (a[i] > max)  max = a[i];  }  ctsort(a,8,max+1);  for (i = 0;i < 8;i ++)  printf("%d\n",a[i]);  
}  

---

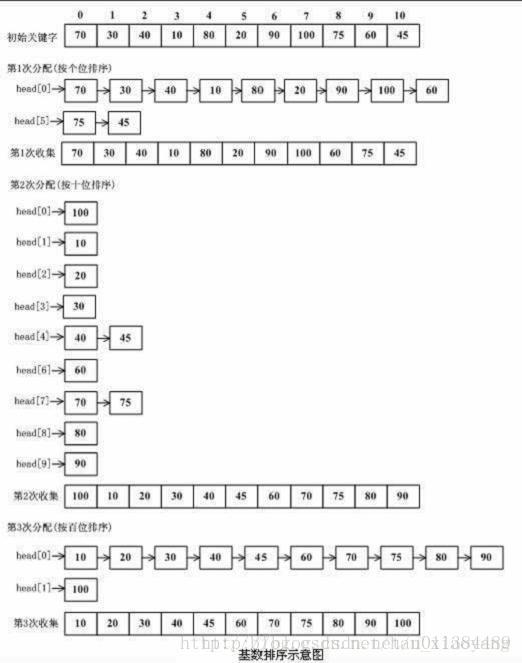
13. 基数排序 (Radix Sort)：

13.1 原理简介：

基数排序是一种非比较型整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。由于整数也可以表达字符串（比如名字或日期）和特定格式的浮点数，所以基数排序也不是只能使用于整数。

算法过程描述如下：

1. 将所有待比较数值（正整数）统一为同样的数位长度，数位较短的数前面补零。
2. 从最低位开始，依次进行一次排序。
3. 这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列

基数排序的时间复杂度是 O(k•n)，其中n是排序元素个数，k是数字位数。

注意这不是说这个时间复杂度一定优于O(n·log(n))，因为k的大小一般会受到n的影响。 以排序n个不同整数来举例，假定这些整数以B为底，这样每位数都有B个不同的数字，k就一定不小于logB(n)。由于有B个不同的数字，所以就需要B个不同的桶，在每一轮比较的时候都需要平均n·log2(B) 次比较来把整数放到合适的桶中去，所以就有：
k 大于或等于 logB(n)
每一轮(平均)需要 n·log2(B) 次比较
所以，基数排序的平均时间T就是：
T>=logB(n)·n·log2(B) = log2(n)·logB(2)·n·log2(B) = log2(n)·n·logB(2)·log2(B) = n·log2(n)
所以和比较排序相似，基数排序需要的比较次数：T ≥ n·log2(n)。 故其时间复杂度为 Ω(n·log2(n)) = Ω(n·log n) 。

13.2 代码实现：

#include <stdio.h>   
#include <stdlib.h>   
void radixSort(int data[]) {  int temp[10][10] = {0};   int order[10] = {0};   int n = 1;   while(n <= 10) {   int i;  for(i = 0; i < 10; i++) {   int lsd = ((data[i] / n) % 10);   temp[lsd][order[lsd]] = data[i];   order[lsd]++;   }   // 重新排列  int k = 0;  for(i = 0; i < 10; i++) {   if(order[i] != 0)  {  int j;  for(j = 0; j < order[i]; j++, k++) {   data[k] = temp[i][j];   }   }  order[i] = 0;   }   n *= 10;   }       
}  
int main(void) {   int data[10] = {73, 22, 93, 43, 55, 14, 28, 65, 39, 81};   printf("\n排序前: ");   int i;  for(i = 0; i < 10; i++)   printf("%d ", data[i]);   putchar('\n');   radixSort(data);  printf("\n排序後: ");   for(i = 0; i < 10; i++)   printf("%d ", data[i]);   return 0;   
}   

13.3 面试例题：

计数排序在处理密集整数排序的问题的时候非常有限，尤其是有时候题目对空间并不做太大限制，那使用计数排序能够达到O(n)的时间复杂度，远快于所有基于比较的其他排序方法。

---

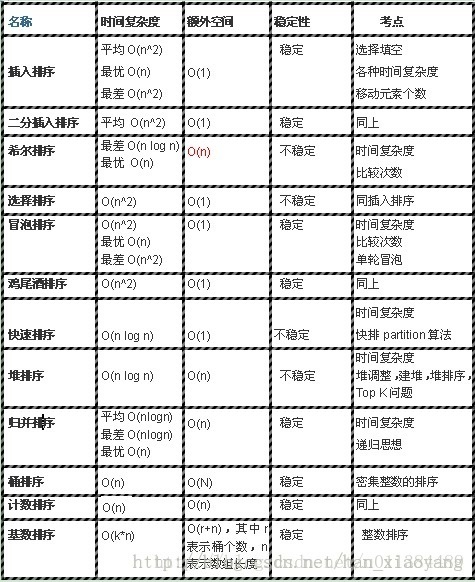
14. 总结：

---

References. ：

• [ 1 ]. Coursera | Java程序设计 | PKU
• [ 2 ]. 转载自：八大排序算法
• [ 3 ]. 转载自：12种排序算法详解

这篇关于【基础算法】(04) 十二种排序算法（第四篇）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---