本文主要是介绍概率分析和随机算法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
雇佣问题
概率分析
随机算法
生日悖论
随机算法
概率分析
球与箱子
总结
雇佣问题
有n个候选人面试,如果面试者比目前雇佣者的分数高,评价更好,那么就辞掉当前雇佣者,而去聘用面试者,否则继续面试新的候选人。面试完n个人结束。
best为到i个候选人中最佳面试者, a数组时候选人名单。
起始条件:best= a[0]; 聘用第一个面试者。
保持:if(best < a[i]) best = a[i]; 聘用面试者。
终止条件:当i == n 时,迭代终止。
代码:
#include "stdio.h"void main() {int best = 0;int n = 10;int a[10] = {0};for (size_t i = 0; i < n; i++){scanf("%d", &a[i]);if(best < a[i]) {best = a[i];}}}
算法分析:
| 代码 | 代价 | |
| 面试 | scanf("%d", &a[i]); | C1 |
| 雇佣 | best = a[i]; | C2 |
假如面试过程中有m个人被雇佣,则总的代价=O(c1*n + c2*m).(0<m<=n)
最坏情况分析:
m=n时,总的代价最大,此时为O(c1*n + c2*n). 由于c1远小于c2,因此总代价为O(c2*n).
平均情况分析:
求平均情况就是求m=1~n的所有可能的均值。在数学中求平均值可以转化为求一个参量的期望。那如何求这个期望值呢?
概率分析
一个面试者是否面试通过服从二项分布。
m个雇佣者的被雇佣的概率
| Xi | 0 | 第1个 | 第2个 | 第n个 |
| P | 0 | 1 | 1/2 | 1/n |
E[X] = E[X1] + E[X2] + … +E[Xn] = 1+1/2+…+1/n = lnx + O(1).
随机算法
代码:
#include "stdio.h"
#include "math.h"
#include <time.h>void permute_by_sorting(int p[10], int a[10]);
void swap(int *a, int *b);
void main() {int best = 0;int rank = 0;int n = 10;int a[10] = {5,2,3,1,4,9,8,10,7,6};int p[10] = {0};permute_by_sorting(p, a);for (size_t i = 0; i < n; i++){if(best < a[i]) {best = a[i];rank = i;}}printf("\nThe best hired man is %dth %d", rank, best);}void permute_by_sorting(int p[10], int a[10]) {int count = 10;srand(time(0));for (size_t i = 0; i < count; i++){p[i] = rand()%1000;printf("%d, ", p[i]);}printf("\n");for (size_t i = 0; i < count; i++){for (size_t j = i; j < count; j++){if(p[i] > p[j]) {swap(&p[i], &p[j]);swap(&a[i], &a[j]);}}printf("%d ", a[i]);}}void swap(int *a, int *b) {int temp;temp = *a;*a = *b;*b = temp;
}
输出结果:
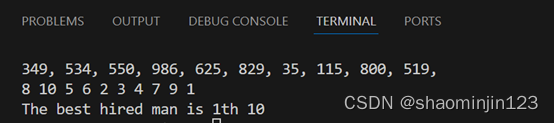

随机排列数列:
可以从输出结果看出,每次出现的优先级的数列不一样,是随机的。样本空间为n!种排列方式,也就是全排列方式,这样就形成了随机算法了,可以使用概率分析算法的性能,每次出现的排列的概率都是1/n!。
以下两行代码能够执行到的次数m的期望E(X)= O(lnx).
best = a[i];rank = i;
生日悖论
问题描述:一个屋子里,必须要有多少人以上,才可以至少有生日相同的两个人?
随机算法
代码
#include "stdio.h"
#include "math.h"
#include <time.h>#define PERSON_NUM 40
void permute_by_sorting(int p[10]);void main() {int same_birthday_p1 = -1;int same_birthday_p2 = -1;int n = PERSON_NUM;int p[PERSON_NUM] = {0};permute_by_sorting(p);for (size_t i = 0; i < n; i++){for (size_t j = i+1; j < n; j++){if(p[j] == p[i]) {same_birthday_p1 = i;same_birthday_p2 = j;break;}}}printf("\nThe best hired man is %d and %d", same_birthday_p1, same_birthday_p2);}void permute_by_sorting(int p[PERSON_NUM]) {int count = PERSON_NUM;srand(time(0));for (size_t i = 0; i < count; i++){p[i] = rand()%365;printf("%d, ", p[i]);}}
PERSON_NUM设为10和40的输出结果:


概率分析
i人和j人两个生日相等且在r日的概率 P[r]= 1/365*1/365. 令n=365. P[r]=1/n*n.
而i人和j人生日相等的情况有1,2,3…,365种,所以P = P[r]*n = 1/n.
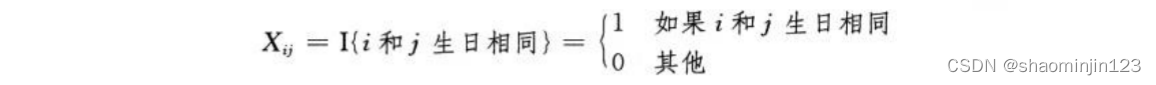
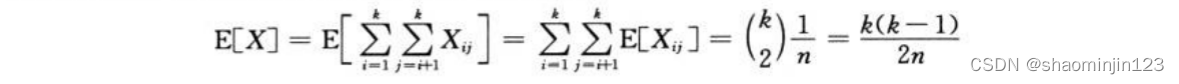
以下的代码中,最后执行了判断语句中的语句时,有X个人相同的期望值为E[X].
E[X]= k(k-1)/(2*n) (PERSON_NUM = k, n = 365).
if(p[j] == p[i]) {same_birthday_p1 = i;same_birthday_p2 = j;break;
}
我在代码中将PERSON_NUM设为10和40的输出结果
| PERSON_NUM | E(X) | 结果 |
| 10 | 0.1232876712328767 | 没有相同生日的人 |
| 40 | 0.4931506849315068 | 有相同生日的人 |
房间中人数为40人时,出现生日相同的期望为1/2,而10人时期望仅为1/10.我输入两次得出生日的结果也与概率模型预期匹配。
球与箱子
问题描述:有b个箱子,往一个指定的箱子中投入球的概率为1/b,投出n个相同的求,指定箱子中有k个球,求k值的期望值。
k正好符合二项分布,b(n,1/b); 所以k的期望值E(K) = n/b.

总结
本文以雇佣问题,生日悖论和球与箱子问题入手,着重讲述如何使用概率方法分析随机算法。
这篇关于概率分析和随机算法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









