本文主要是介绍内涵：目标检测之ATSS，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
1. 论文
1.1 文章讲了什么
目前目标检测领域的做法分为两大类：anchor-based(one-stage vs two-stage)和anchor-free(keypoint-based vs center-based)。anchor-based系列的文章有例如R-CNN系列和YOLO系列。而anchor-free系列的文章是由于FPN和Focal loss的出现，也变得流行起来（大概在2019年初的样子）。atss这篇文章认为两者的本质其实并没有太大差异，一些看似差异的操作其实并不会对最终的性能产生影响：例如，anchor的数量、基于box回归好还是基于point回归。在两类方法中定义正、负样本的方式不同才是决定二者出现性能差异的原因所在。如果采用相同的定义方式，两类方法的性能并无显著性差异。
在获得上述结论的基础上，作者进一步设计出一种自适应的positive sample方法atss，采用该方法通过一种自适应的策略来定义正样本、副样本，可以获得一个更好的性能。
1.2 文章的思路历程
1.2.1 based 和 free的本质区别在positive sample
要获得该小节标题中的结论，首先要明确anchor-based和 anchor-free两者的区别是什么，然后才能通过控制变量的方式进行实验，获得结论。总结下来，就是作者认为存在 以下三点差异：
- anchor数量设置
- 基于box回归还是基于point回归
- 定义正负样本的方式
其次是定义本文中的anchor-free指的是什么。之所以要指明这一问题，原因在于anchor-free分为两大类:keypoint-based和center-based。对于keypoint-based，它走的是标准的关键点估计的pipeline，与anchor-based的探测器方法基本上毫无关系。而center-based的方法与anchor-based的方法是相似的，具有可比较性。因此本文的anchor-free指的是是anchor-based的探测器方法。
作者以center-based中的FCOS和anchor-based 中的RetinaNet为例，两者的区别在于：
- several anchor boxes vs one anchor point per location。
- the definition of positive and negative samples。
- The regression starting status. anchor box vs anchor point
但因为FCOS和RetinaNet并不是同一时期的文章，前者偏后，因此纳入了很多的新的tircks，例如GIOU LOSS、GROUP NORM等。作者将这些额外的通用操作都加入到RetinaNet中。RetinaNet在加了这些操作之后，可以从37.0%。而FCOS的性能为37.8%。
在先将额外操作对齐之后，真正的实验开始。此时FCOS和RetinaNet（anchor数量设置为1）的差异只剩下两个：
- 分类任务中如何定义正、副样本
- 回归任务中一个从anchor进行回归，一个从anchor point进行回归
首先来看，两者是如何定义正样本的 ：
如果用文字描述，RetinaNet的正、负样本策略可以进行如下描述：
| 正样本 | 负样本 | 忽略 |
|---|---|---|
| anchor box（这里应该是指预测值）为IOU最大，或者IOU阀值>p | IOU阈值<n | n<IOU阈值<p |
FCOS的正、负样本策略可以进行如下描述:
step1: 预测的anchor points在ground-truth box内部，作为候选的正样本（其他的都舍弃掉了？）
step2:候选anchor points通过与没一个金字塔预先设定好的超参数–scale range进行比较，满足则为正样本，不满足则为副样本。
针对正、负样本的采样方式，作者做了对比实验，结果如下图所示，可以看到RetinaNet的策略从iou变为Spatial and Scale Constraint，其性能就会提升0.8个点，与FCOS的性能一致。FCOS的策略变化以及其对应结果也同样。从而证明了FCOS为代表的anchor-free的方法，其优势仅仅在于正、负样本策略的差异，前者更优；同时point开始回归还是box开始回归也不重要了。
再来看，anchor 数量的影响，上面的结论实验的前提是RetinaNet的anchor的数量退化为1（为了和anchor-free配置对齐）。
实验结果如上表所示，这两行的意思：第一行,将RetinaNet的anchor设置为9（我们不太关心），第二行是在此基础上添加FCOS所使用的通用优化手段，此时性能为38.4%，这个实验是可以与37.0%相比较的，说明anchor从1设置为9个，是有一个比较大的提升的。
1.2.2 一种更好的postive sample策略： ATSS
紧接着，作者回到“如何定义正、负样本"这个的问题上，提出了ATSS”，这是本文的主要创新点。这种方式的优点是没有超参数（对于anchor-based就是Iou阈值，对于anchor-free来讲就是scale range，一旦选定，规则就固定下来），是一种自适应的策略，对不同的检测场景撸棒。
这里需要注意atss策略，中心距离会兼顾了anchor-based和anchor-free。再有就是注意到，会有额外的限制：见12行，需要anchor box的中心要在ground truth boxes里面。另外如果一个anchor box匹配到不同的ground-truth boxes，需要 选择最高的那个IOU。（这个编写代码的时候可能会绕一下）
上面是介绍了如何做，下面介绍为什么这样做：因为按照统计学的理论，对于正太分布，大于等于均值+方差的数据会占15%，（或者16%，这也是本篇文章的封面为什么会选择一个正太分布的曲线）。虽然候选框的中心距离分布不是正太分布，但实验下来，正样本稳定在20%左右。这样做会带来什么样的好处：几乎达到了无超参需要设置的效果，参数是自适应的。
其实在通往param-free的路上还有一个阻碍：超参数k（也就是候选者的数量），但马上作者通过实验证明，该参数的设置可以比较随意，不会对实验结果产生很大的影响。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传
使用atss的结果到底如何
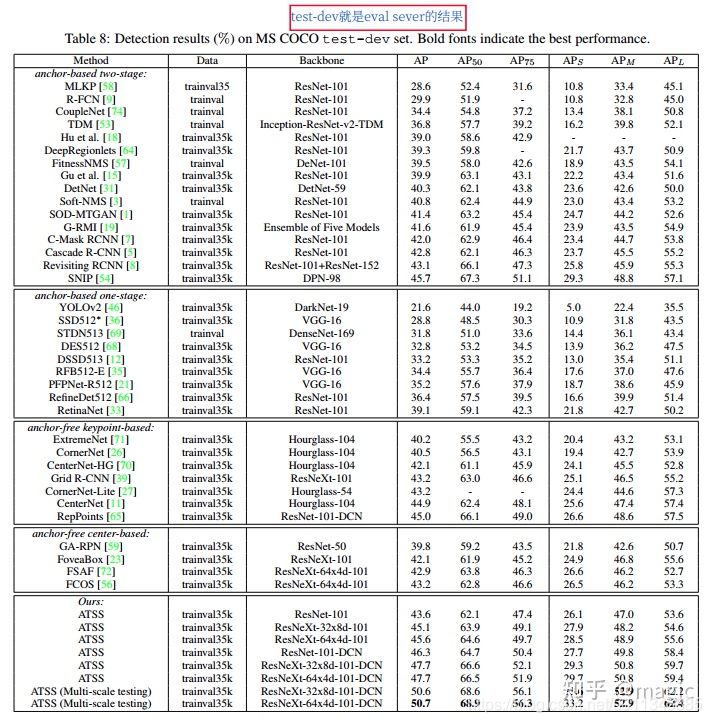
可以看到对于RetinaNet在使用了IOU Loss和group norm之后，使用了atss之后，依然可以张点2.3,挺不容易的啦。对于FCOS,也可以继续涨点1.4。其效果还是客观的。但需要注意的是，对于FCOS，作者在论文中讲的是，候选依然使用的inner内部，在sample 正样本的时候采用了atss。
1.2.3 anchor 数量 与 atss 消融实验
至此，对于anchor-free来，atss就直接使用了，效果上面已经证明了。对于anchor-based来讲，box的数量多设置点（从1到9）和使用atss都有提升效果。两者放到一起会有1+1=2的效果吗？如下表的消融实验显示并没有（见第4行和第7行）：
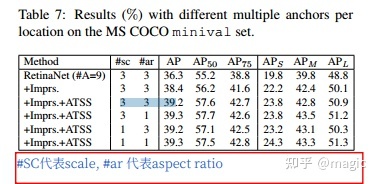
使用atss并不会带来额外的计算量，在atss上机上更多的anchor数量，无上升效果。因此后续anchor-base网络的默认配置可以设置为anchor数量为1, 然后正负样本的选用策略使用atss。
2. 官方代码
官方代码已经fork了一份到私有仓库：https://github.com/johnson-magic/ATSS.git dev分支（修复了一些官方版本不兼容的问题，推荐使用）
我按照官方的指导，训练了下ATSS_R_50_FPN_1x版本的模型，结果基本与官方的性能对齐38.9%（官方说法为39.3%）。
这篇关于内涵：目标检测之ATSS的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
![[数据集][目标检测]血细胞检测数据集VOC+YOLO格式2757张4类别](https://i-blog.csdnimg.cn/direct/22c867ab717d44c78b985ed667169b42.png)
