本文主要是介绍旋转矩阵简单可视化与平移向量方向问题探讨,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
接触了SLAM好久了,但是对于变换矩阵和平移矩阵始终觉得没有完全理解透彻,刚好碰到了因为理解导致的错误,就借此再整理一下!
直接开始!
1.只有平移时:
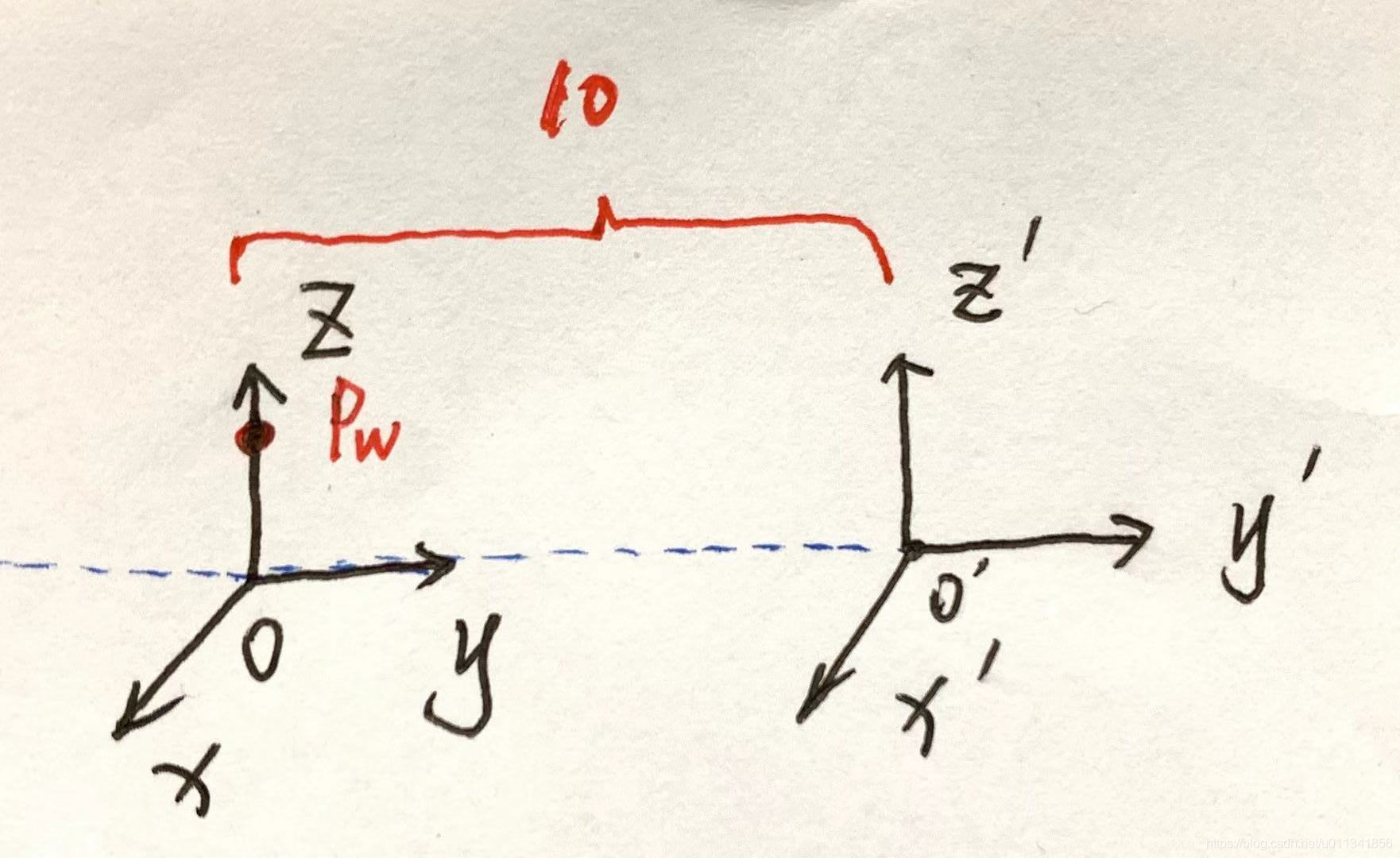
注意:不论在哪个坐标系中表示空间中的一个点,都不会改变这个点的位置,只是在不同的坐标系中,坐标值会不一样,请仔细理解一下!
O ′ − x ′ y ′ z ′ O'-x'y'z' O′−x′y′z′坐标系就是将 O − x y z O-xyz O−xyz坐标系沿着 y y y轴向右平移10个单位。
P w P_w Pw在 O − x y z O-xyz O−xyz坐标系下的坐标值为 [ 0 , 0 , 1 ] T [0,0,1]^T [0,0,1]T;
P w P_w Pw在 O ′ − x ′ y ′ z ′ O'-x'y'z' O′−x′y′z′坐标系的坐标值为 [ 0 , − 10 , 1 ] T [0,-10,1]^T [0,−10,1]T,并将该坐标值记做 P c P_c Pc。
P w P_w Pw在两个坐标系下坐标值的关系,可以用如下关系式表示: P c = R c w ∗ P w + t c w (0) P_c = R_{cw} * P_w + t_{cw} \tag 0 Pc=Rcw∗Pw+tcw(0)
由于上述两个坐标系并没有发生旋转变换,所以:
旋转矩阵 R c w = [ 1 0 0 0 1 0 0 0 1 ] R_{cw} = \left[\begin{matrix} 1&0&0 \\0&1&0\\0&0&1 \end{matrix}\right] Rcw=⎣⎡100010001⎦⎤,而平移向量 t c w = [ 0 , − 10 , 0 ] T t_{cw} = [0,-10,0]^T tcw=[0,−10,0]T;
我们可以发现平移向量 t c w t_{cw} tcw是一个 O ′ O' O′指向 O O O的向量。
2.只有旋转时:
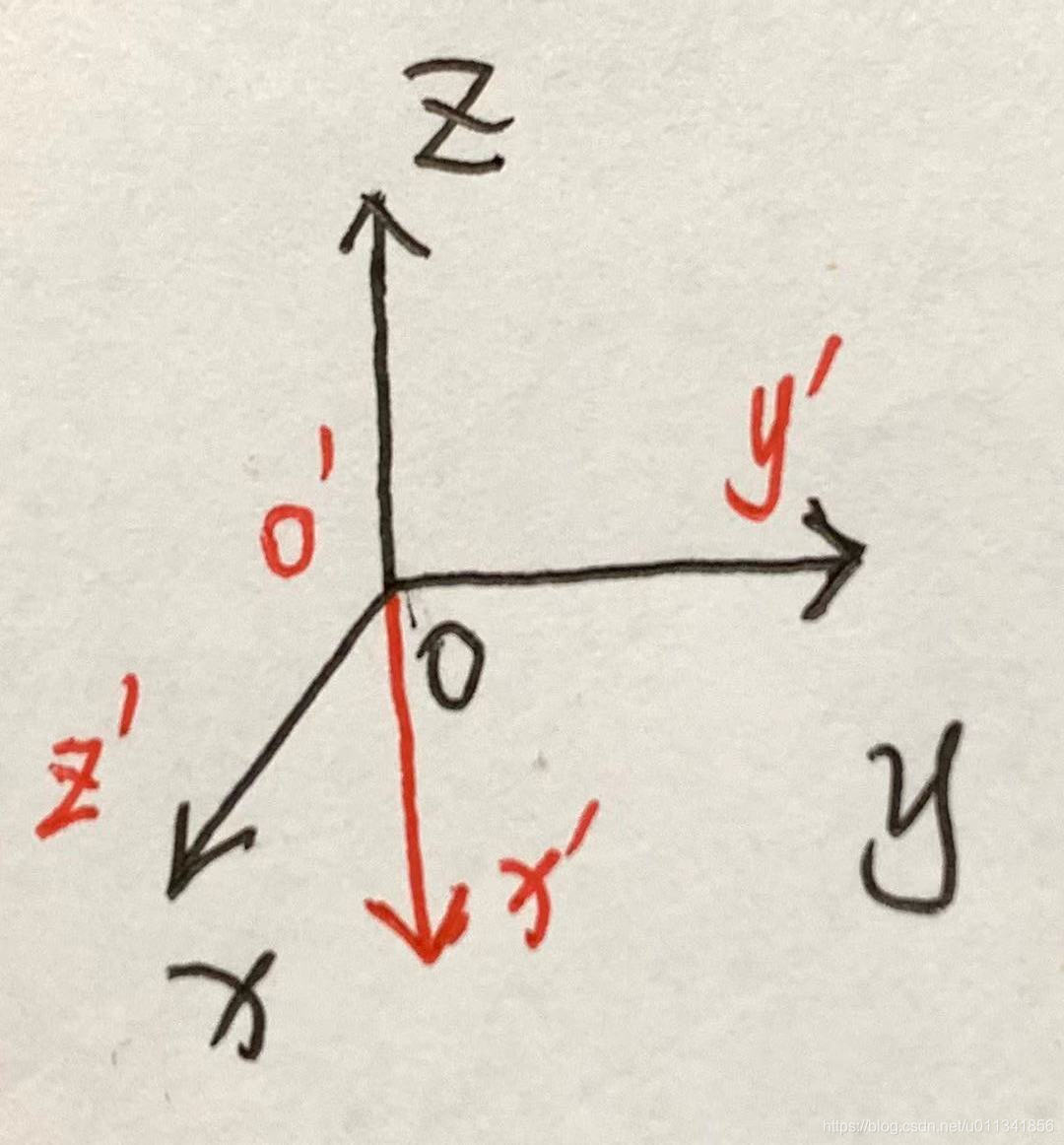
将 O − x y z O-xyz O−xyz坐标系绕着 y y y轴逆时针旋转 90 ° 90\degree 90°得到 O ′ − x ′ y ′ z ′ O'-x'y'z' O′−x′y′z′坐标系。同样的在 O − x y z O-xyz O−xyz坐标系下的一个点 P w = [ 0 , 0 , 1 ] T P_w = [0,0,1]^T Pw=[0,0,1]T,在 O ′ − x ′ y ′ z ′ O'-x'y'z' O′−x′y′z′坐标系下的坐标值为 P c = [ − 1 , 0 , 0 ] T P_c = [-1,0,0]^T Pc=[−1,0,0]T,此时两个点之间的变换满足如下关系式子:
P c = R c w ∗ P w + t c w P_c = R_{cw}*P_w + t_{cw} Pc=Rcw∗Pw+tcw
而 R c w = [ c o s ( − 90 ) 0 s i n ( − 90 ) 0 1 0 − s i n ( − 90 ) 0 c o s ( − 90 ) ] R_{cw}= \left[\begin{matrix}cos(-90)& 0& sin(-90) \\ 0& 1& 0\\ -sin(-90)& 0& cos(-90) \end{matrix}\right] Rcw=⎣⎡cos(−90)0−sin(−90)010sin(−90)0cos(−90)⎦⎤, t c w = [ 0 , 0 , 0 ] T t_{cw}=[0,0,0]^T tcw=[0,0,0]T
即有旋转又有平移

在 O − x y z O-xyz O−xyz坐标系下,有一个点 P w = [ a , b , c ] T P_w=[a,b,c]^T Pw=[a,b,c]T,它在 O ′ − x ’ y ′ z ′ O'-x’y'z' O′−x’y′z′坐标系下的坐标为 P c = [ a ′ , b ′ , c ′ ] T P_c=[a',b',c']^T Pc=[a′,b′,c′]T,同样的它也满足下式子:
P c = R c w ∗ P w + t c w P_c = R_{cw}*P_w + t_{cw} Pc=Rcw∗Pw+tcw
同样的平移向量 t c w t_{cw} tcw依然是 O ′ O' O′指向 O O O
总结
由上面的简单过程,我们可以对 P c = R c w ∗ P w + t c w P_c = R_{cw}*P_w + t_{cw} Pc=Rcw∗Pw+tcw式子这样理解:
R c w ∗ P w R_{cw}*P_w Rcw∗Pw表示将点 P w P_w Pw在 O − x y z O-xyz O−xyz坐标系下的坐标,旋转到 O ′ − x ′ y ′ z ′ O'-x'y'z' O′−x′y′z′坐标系下,也就是用 O ′ − x ′ y ′ z O'-x'y'z O′−x′y′z坐标系下的坐标值来表示 P w P_w Pw点。有一点你需要注意,旋转完之后,两个坐标系的原点依然是重合,因为旋转矩阵不会导致平移。
然后加上平移向量 t c w t_{cw} tcw,就完成了整个旋转和平移变换。对于平移向量方向是 O ‘ O‘ O‘指向 O O O,也就是变换完成之后的坐标系原点指向变换之前坐标系的原点。
当然也有别的理解方式,找到自己习惯的就可以,你也可以自己画图一步一步理解!
这篇关于旋转矩阵简单可视化与平移向量方向问题探讨的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






