本文主要是介绍【代码+详解】算法题 : 最大公约数,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
❗❗❗必看:
下列题我全部都使用 Java 语言写的,并且均可以提交成功,获得Accepted 结果的. 如果代码和详解看了之后,对答案有任何疑问,都可以在评论区提出来,我都会一个一个回答.
❗❗❗感谢大家的支持,如果喜欢我的博客,关注 点赞 收藏 评论一波,非常感谢!!!
文章目录
- 题目:最大公约数
- 样例测试
- 代码
- 图示
- 详解
- 基本思想
- 具体步骤
- 代码解释
题目:最大公约数
给定两个正整数,求它们的最大公约数。
Input
有多组数据,每行为两个正整数,且不超过int可以表示的范围。
Output
行对应输出最大公约数。
样例测试
输入
4 8
8 6
200 300
输出
4
2
100
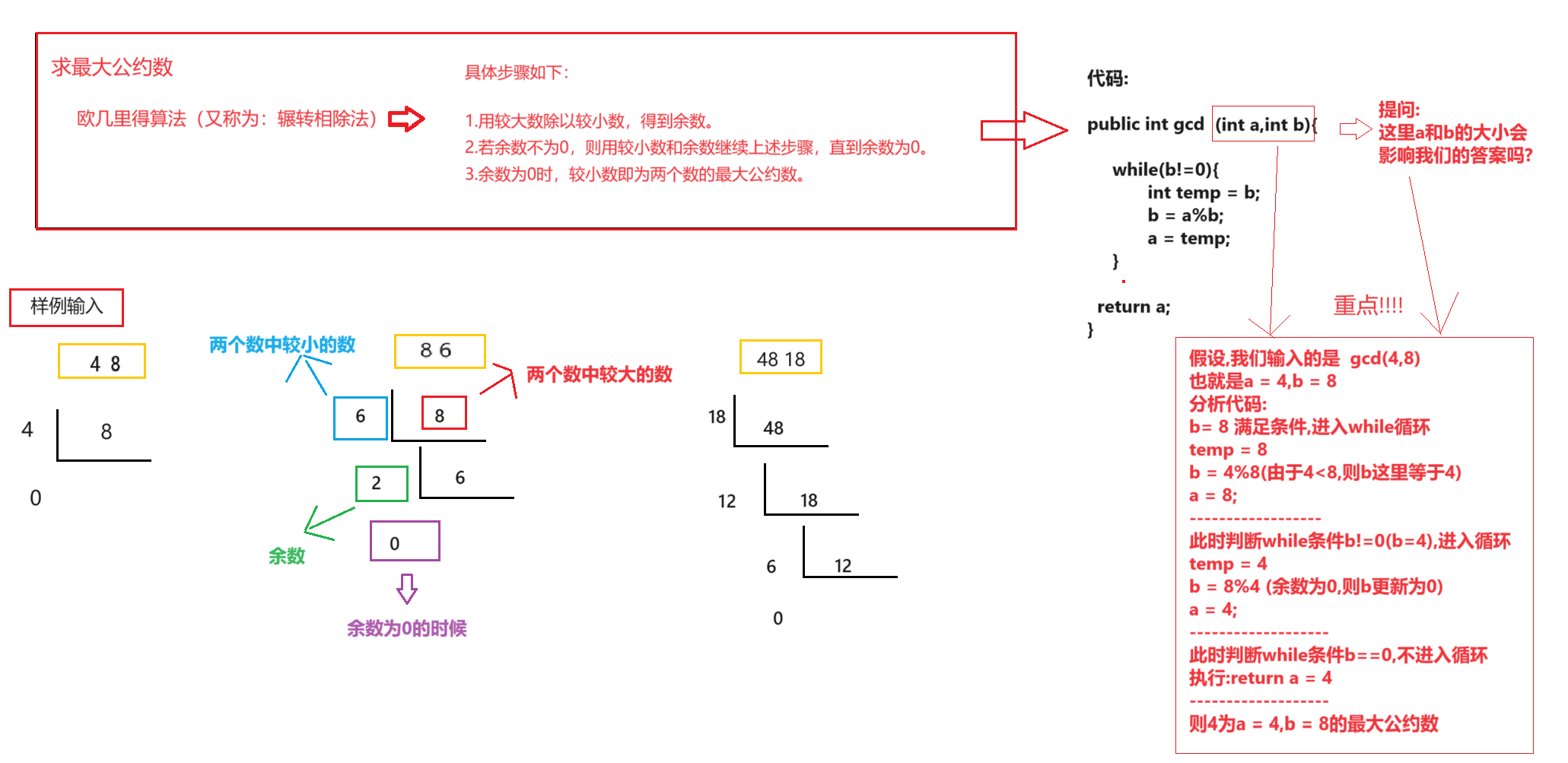
代码
import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);while(scanner.hasNextInt()) {int a = scanner.nextInt();int b = scanner.nextInt();System.out.println(gcd(a,b));}scanner.close();}private static int gcd(int a, int b) {while(b!=0) {int temp = b;b = a%b;a = temp;}return a;}}
图示
详解
这道题目我们可以通过欧几里得算法(也称辗转相除法)来解决。这是一种求两个正整数最大公约数(GCD)的高效算法。
基本思想
这道题目我们可以通过欧几里得算法(也称辗转相除法)来解决。这是一种求两个正整数最大公约数(GCD)的高效算法。
两个数的最大公约数等于其中较小的那个数和两个数相除余数的最大公约数。
具体步骤
- 用较大数除以较小数,得到余数。
- 若余数不为0,则用较小数和余数继续上述步骤,直到余数为0。
- 余数为0时,较小数即为两个数的最大公约数。
代码解释
- 输入处理:
- 使用 Scanner 类从标准输入中读取多组整数对。
- 通过 scanner.hasNextInt() 循环读取输入,直到没有更多整数。
- 欧几里得算法:
- 定义一个 gcd 方法来计算两个整数的最大公约数。
- 使用 while 循环,直到余数 b 为0。
- 在循环内,使用变量 temp 保存当前余数 b,然后更新 b 为 a % b,再将 a 更新为 temp。
- 当 b为0时,a即为最大公约数。
- 输出结果:
- 每对整数计算完成后,直接输出结果。
这篇关于【代码+详解】算法题 : 最大公约数的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






