本文主要是介绍LES大涡模拟基础，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
参考自https://www.bilibili.com/video/BV1EL411A7gu?p=30&vd_source=b624b9d3e49866ce8c6a455f1ab7c03f
如何解析涡
用网格不能解析单元尺度以下的涡（小涡）而只能解析大涡
对于小涡，需要引入亚格子模型
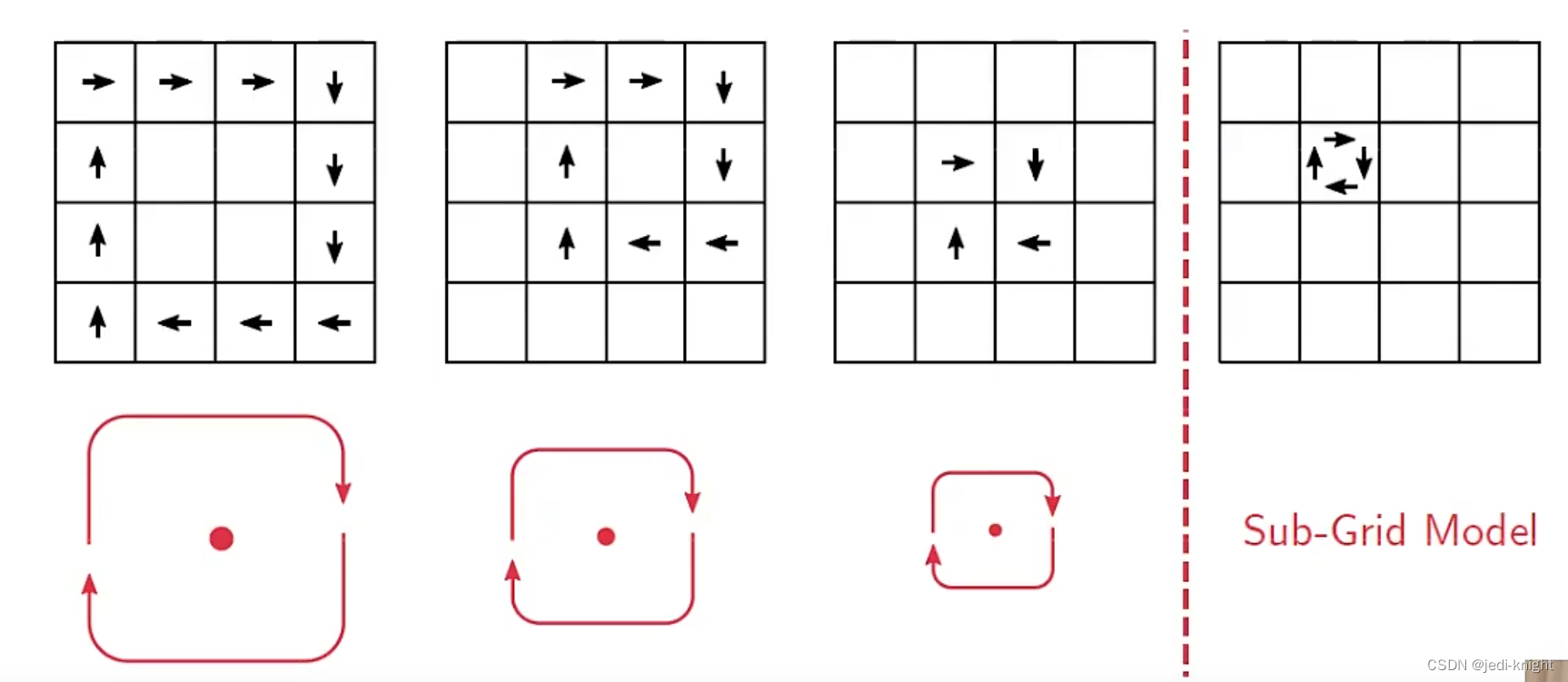
如何选择合适的网格尺寸？
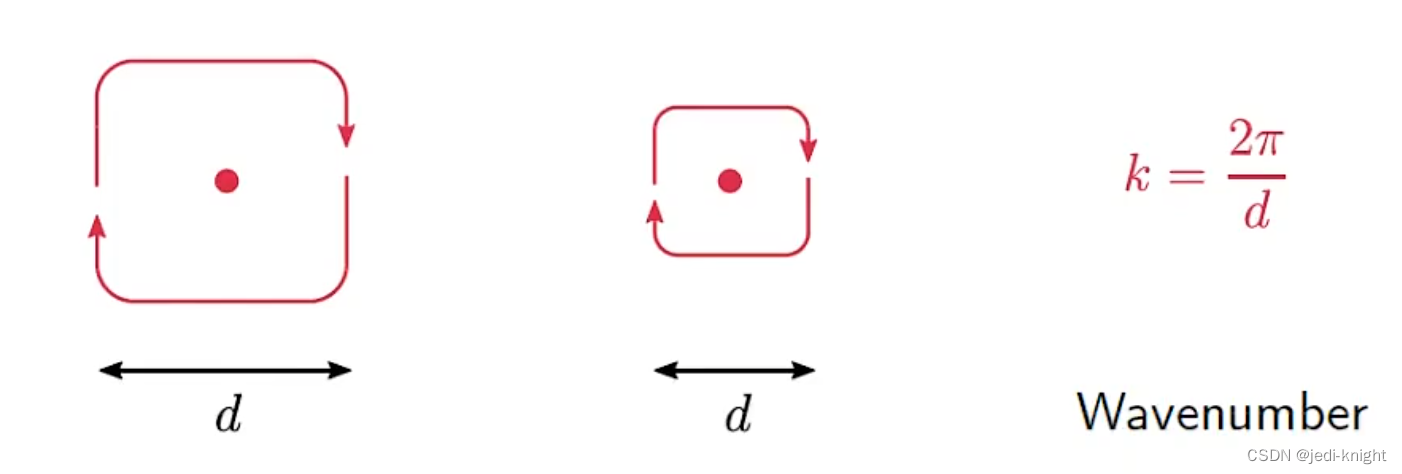
根据湍流能量级联（Turbulant Energy Cascade）选择网格尺寸
注意：小波具有更高的波数
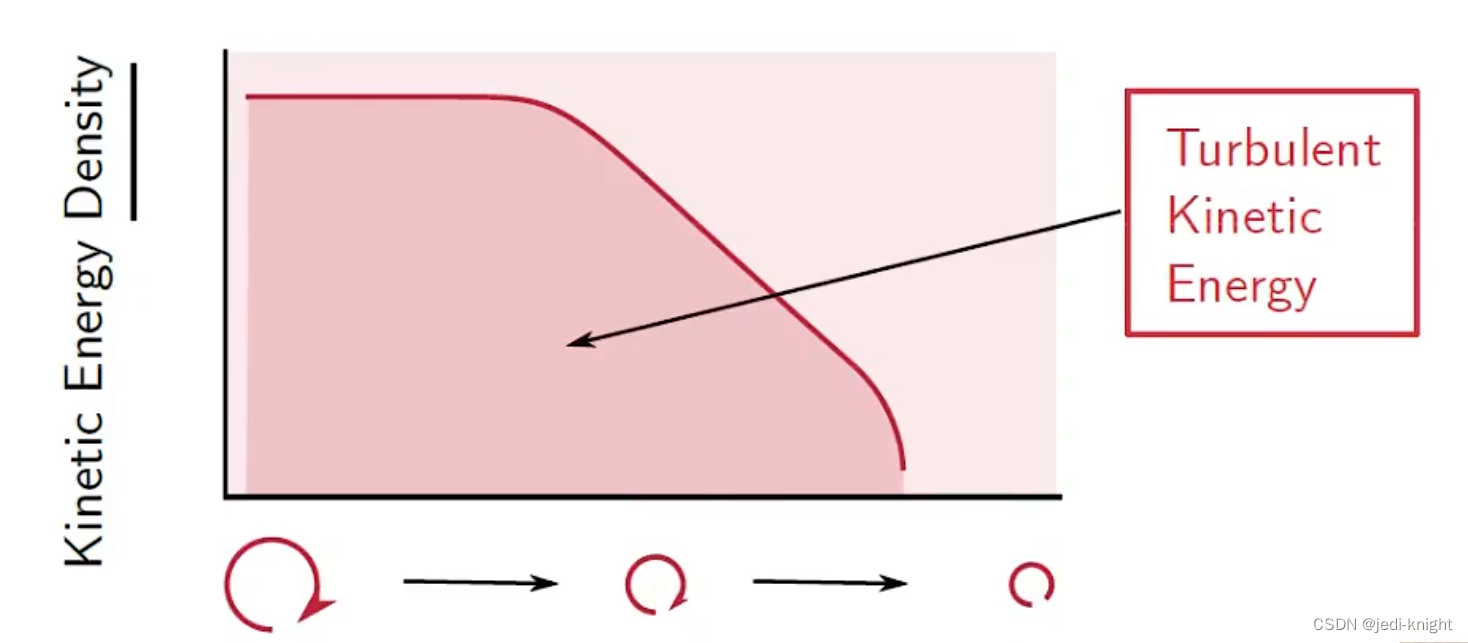
RANS的想法是不解析涡，而是直接添加湍流动能输运方程描述每一点的湍动能。某一点的湍动能是对该点处所有大小的涡的动能求和。
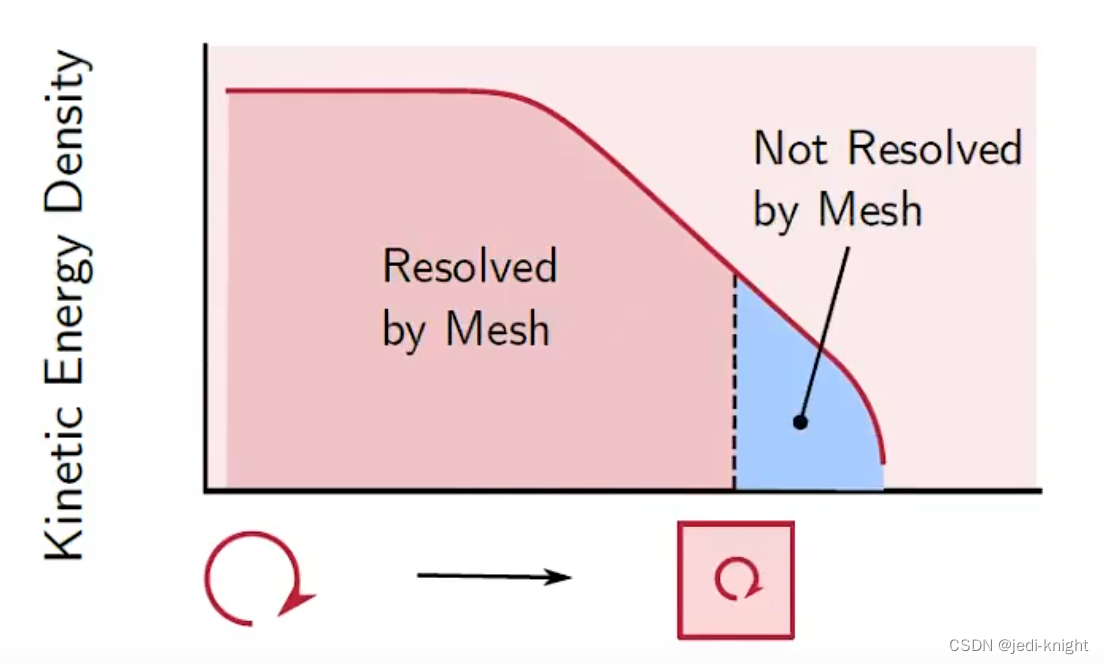
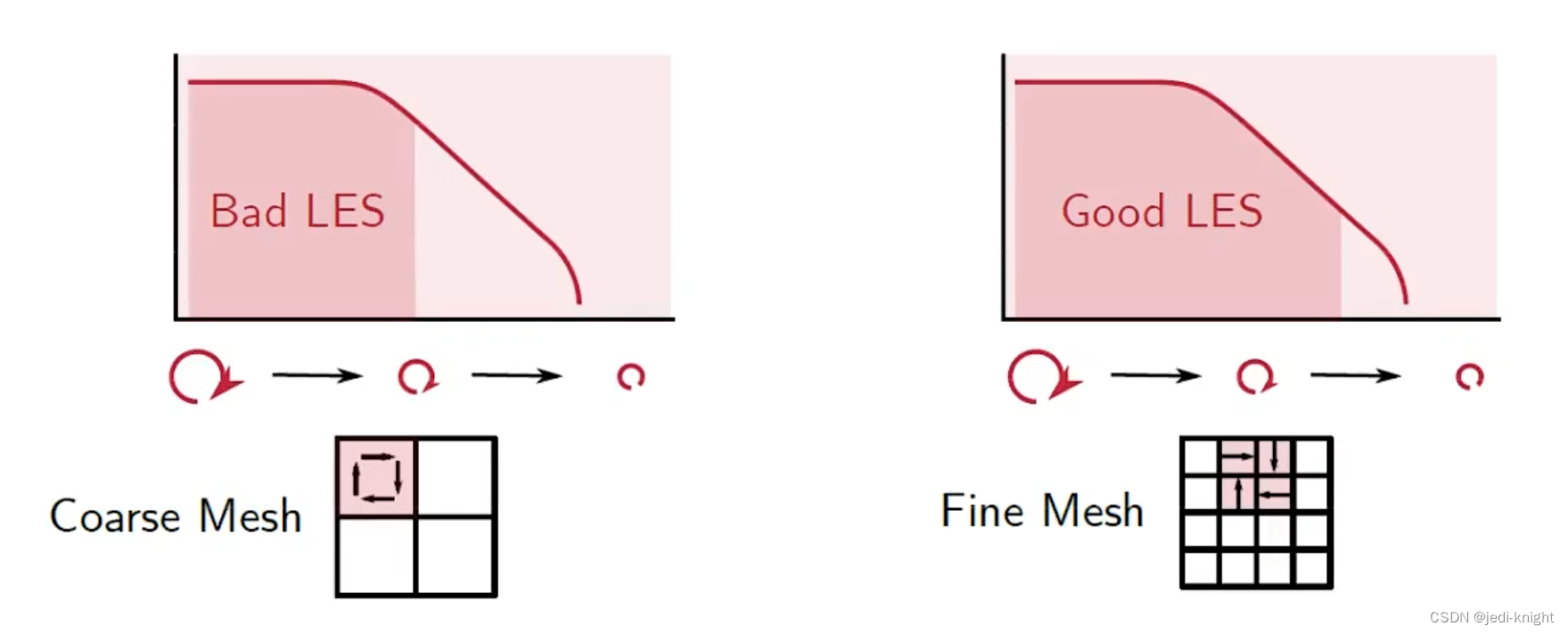
LES的想法是解析大涡，用亚格子模型描述小涡。好的LES网格应当能解析80%以上的大涡能量。所以LES的网格要比RANS细。
在判断网格是否合适时，需要引入积分长度尺度（Intergral Length Scale）。在使用LES计算前，需要用RANS计算积分长度尺度，以判断网格是否合适
l 0 = k 3 / 2 ϵ l_{0}=\frac{k^{3 / 2}}{\epsilon} l0=ϵk3/2 l 0 = k 1 / 2 C μ ω l_{0}=\frac{k^{1 / 2}}{C_{\mu} \omega} l0=Cμωk1/2
如果在积分长度上布置5个网格，可以达到要求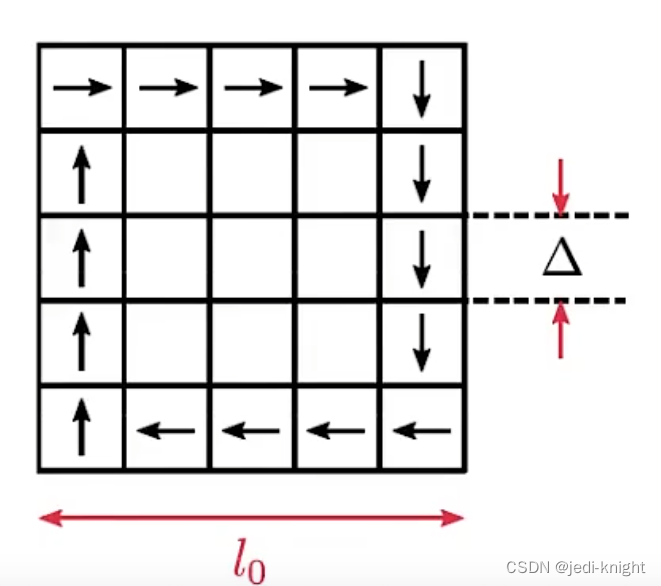
在具体评估网格质量时，可以定义如下的一个场。如果f小于5，那么说明此处网格需要加密
f = l 0 Δ = k 3 / 2 ϵ ∗ Δ Δ = Cell Volume 1 / 3 f=\frac{l_{0}}{\Delta}=\frac{k^{3 / 2}}{\epsilon * \Delta} \quad \Delta=\text { Cell Volume }^{1 / 3} f=Δl0=ϵ∗Δk3/2Δ= Cell Volume 1/3
在LES计算之后评估网格
当然也可以在LES计算完成之后评估网格。首先计算网格能解析的大涡的湍动能
k res = 1 2 ( u ′ u ′ ‾ + v ′ v ′ ‾ + w ′ w ′ ‾ ) k_{\text {res }}=\frac{1}{2}\left(\overline{u^{\prime} u^{\prime}}+\overline{v^{\prime} v^{\prime}}+\overline{w^{\prime} w^{\prime}}\right) kres =21(u′u′+v′v′+w′w′)
总的湍动能由下式计算
k = k res + k sgs k=k_{\text {res }}+k_{\text {sgs }} k=kres +ksgs 如果 k res k_{\text {res }} kres 占比超过80%，那么网格无需加密
亚格子模型
目标：为了刻画“可解析”的大涡破碎成为“不可解析”的小涡的过程
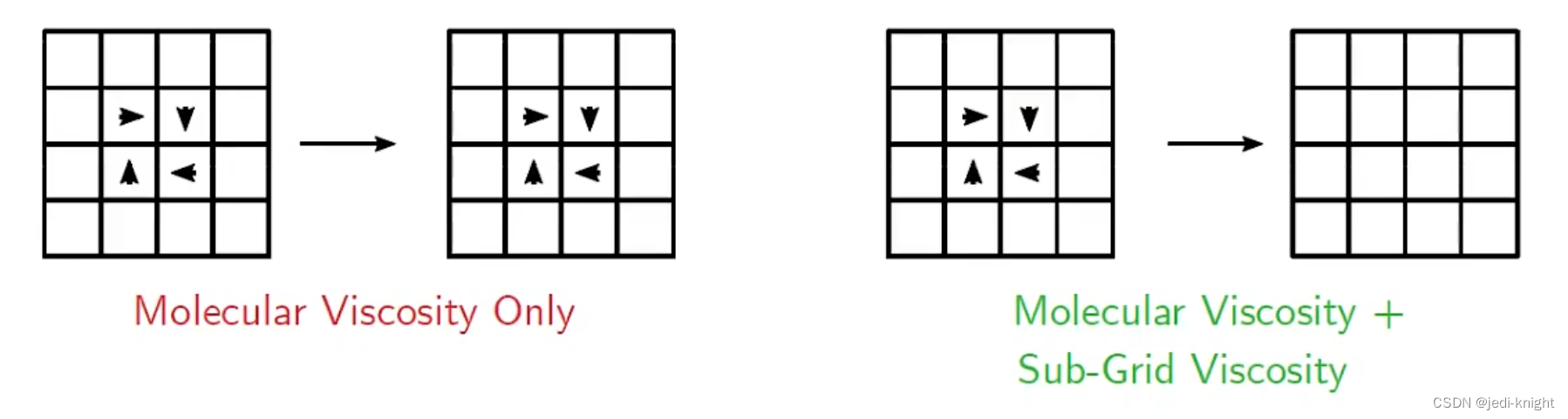
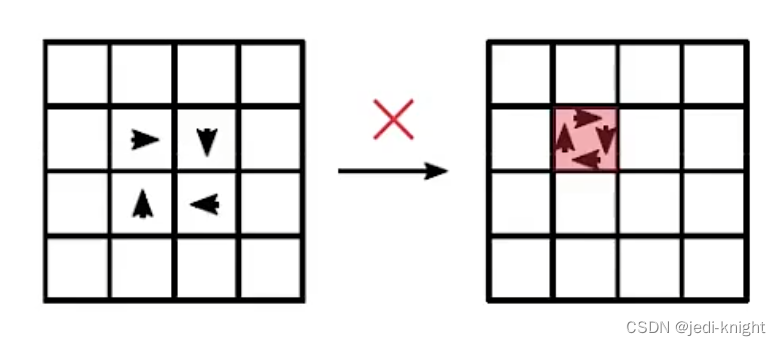措施：在粘度的基础上添加亚格子粘性，以模拟最小涡的破碎
∂ ( ρ U i ) ∂ t + ∂ ∂ x j ( ρ U i U j ) = − ∂ P ∂ x i + ∂ ∂ x j ( τ i j + τ s g s ) ⏟ Viscous + Sub-Grid \frac{\partial\left(\rho U_{i}\right)}{\partial t}+\frac{\partial}{\partial x_{j}}\left(\rho U_{i} U_{j}\right)=-\frac{\partial P}{\partial x_{i}}+\underbrace{\frac{\partial}{\partial x_{j}}\left(\tau_{i j}+\tau_{s g s}\right)}_{\text {Viscous + Sub-Grid }} ∂t∂(ρUi)+∂xj∂(ρUiUj)=−∂xi∂P+Viscous + Sub-Grid ∂xj∂(τij+τsgs) τ s g s = 2 ρ ν s g s S i j ⋆ − 2 3 ρ k s g s δ i j S i j ⋆ = 1 2 ( ∂ U ~ i ∂ x j + ∂ U ~ j ∂ x i − 1 3 ∂ U ~ k ∂ x k δ i j ) \tau_{s g s}=2 \rho \nu_{s g s} S_{i j}^{\star}-\frac{2}{3} \rho k_{s g s} \delta_{i j} \quad S_{i j}^{\star}=\frac{1}{2}\left(\frac{\partial \tilde{U}_{i}}{\partial x_{j}}+\frac{\partial \tilde{U}_{j}}{\partial x_{i}}-\frac{1}{3} \frac{\partial \tilde{U}_{k}}{\partial x_{k}} \delta_{i j}\right) τsgs=2ρνsgsSij⋆−32ρksgsδijSij⋆=21(∂xj∂U~i+∂xi∂U~j−31∂xk∂U~kδij)
亚格子粘度 ν s g s \nu_{s g s} νsgs由亚格子模型决定，通常与网格尺寸有关。所以LES通常不进行网格无关性验证，因为不同网格下亚格子粘度会变化。
这篇关于LES大涡模拟基础的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
