本文主要是介绍【数据结构】从前序与中序遍历,或中序与后序遍历序列,构造二叉树,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
欢迎浏览高耳机的博客
希望我们彼此都有更好的收获
感谢三连支持!


首先,根据先序遍历可以确定根节点E,再在中序遍历中通过E确定左树和右数 ;
设立inBegin和inEnd,通过这两个参数的游走,来进行子树的创建;
已知根节点,则左子树的范围表示为(inBegin,rootIndex - 1);
而右子树为(rootIndex + 1,inEnd);
通过递归调用,即可不断创建子树,直到叶子节点;
如果inBegin > inEnd,则说明此时为叶子节点,应该返回上一层递归;
public TreeNode buildTree(int[] preorder, int[] inorder) {return buildTreeChilde(preorder, inorder, 0, inorder.length-1);
}private TreeNode buildTreeChilde(int[] preorder, int[] inorder, int inBegin, int inEnd) {if(inBegin > inEnd){return null;}TreeNode root = new TreeNode(preorder[preIndex]); // 创建根节点int rootIndex = findRootIndex(inorder, inBegin, inEnd, preorder[preIndex]); // 找到根节点在中序遍历中的位置preIndex++;root.left = buildTreeChilde(preorder, inorder, inBegin, rootIndex-1); // 递归构建左子树root.right = buildTreeChilde(preorder, inorder, rootIndex+1, inEnd); // 递归构建右子树return root;
}private int findRootIndex(int[] inorder, int inBegin, int inEnd, int key){for (int i = inBegin; i <= inEnd; i++) {if (key == inorder[i]) {return i;}}return -1;}OJ链接:
https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/description/
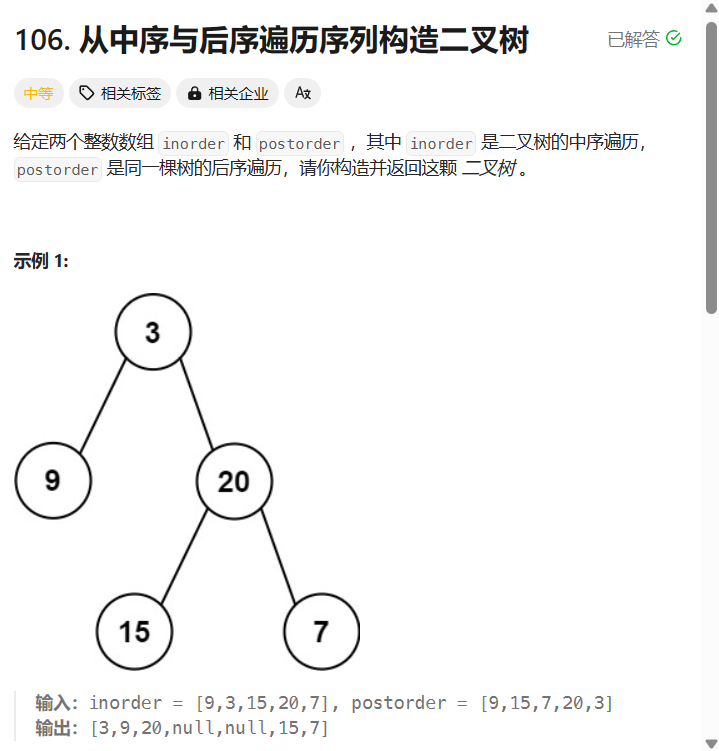

同样的,根据后序遍历可以确定根节点,再在中序遍历中通过根节点确定左树和右数 ;
需要注意的是,由于postIndex根据后序遍历(左,右,根)创建,与前序遍历相反,所以每次递归时postIndex--,从根节点前的右子树开始递归;
同样的,已知根节点,则右子树表示范围为(rootIndex + 1,inEnd);
而左子树表示为(inBegin,rootIndex - 1);
通过递归调用,即可不断创建子树,直到叶子节点;
如果inBegin > inEnd,则说明此时为叶子节点,应该返回上一层递归;
public TreeNode buildTree(int[] inorder, int[] postorder) {postIndex = postorder.length-1;return buildTreeChilde(inorder, postorder, 0, inorder.length-1);
}private TreeNode buildTreeChilde(int[] inorder, int[] postorder, int inBegin, int inEnd) {if(inBegin > inEnd){return null;}TreeNode root = new TreeNode(postorder[postIndex]); // 创建根节点int rootIndex = findRootIndex(inorder, inBegin, inEnd, postorder[postIndex]); // 找到根节点在中序遍历中的位置postIndex--;root.right = buildTreeChilde(inorder, postorder, rootIndex+1, inEnd); // 递归构建右子树root.left = buildTreeChilde(inorder, postorder, inBegin, rootIndex-1); // 递归构建左子树return root;
}private int findRootIndex(int[] inorder, int inBegin, int inEnd, int key){for (int i = inBegin; i <= inEnd; i++) {if (key == inorder[i]) {return i;}}return -1;}OJ链接:https://leetcode.cn/problems/construct-binary-tree-from-inorder-and-postorder-traversal/description/
希望这篇博客能为你理解java编程思想提供一些帮助。
如有不足之处请多多指出。
我是高耳机。
这篇关于【数据结构】从前序与中序遍历,或中序与后序遍历序列,构造二叉树的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







