NYOJ 题目17 单调递增最长子序列 （DP） hdu 题目2845 Bean

本文主要是介绍NYOJ 题目17 单调递增最长子序列 （DP） hdu 题目2845 Bean，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

描述

Bean-eating is an interesting game, everyone owns an M*N matrix, which is filled with different qualities beans. Meantime, there is only one bean in any 1*1 grid. Now you want to eat the beans and collect the qualities, but everyone must obey by the following rules: if you eat the bean at the coordinate(x, y), you can’t eat the beans anyway at the coordinates listed (if exiting): (x, y-1), (x, y+1), and the both rows whose abscissas are x-1 and x+1.


Now, how much qualities can you eat and then get ?

输入

There are a few cases. In each case, there are two integer M (row number) and N (column number). The next M lines each contain N integers, representing the qualities of the beans. We can make sure that the quality of bean isn't beyond 1000, and 1<=M,N<=500.

输出

For each case, you just output the MAX qualities you can eat and then get.

样例输入

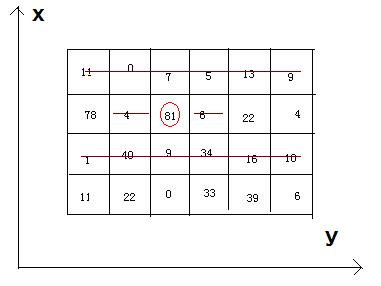
4 6
11 0 7 5 13 9
78 4 81 6 22 4
1 40 9 34 16 10
11 22 0 33 39 6

样例输出

242

二次dp，

1.首先单独对每行的数据进行DP处理，得到一个最大值；

2,.每行的最大值又组成一个新的数组，再次dp求最大值

 
#define N 505
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
int MAX(int x,int y){return x>y?x:y;
}
int main()
{int m,n,i,j,k,max,a[N][N],dp[N][2],f[N]; while(scanf("%d%d",&m,&n)!=EOF){for(i=0;i<m;i++) for(j=0;j<n;j++)scanf("%d",&a[i][j]);for(i=0;i<m;i++) {dp[0][0]=0; dp[0][1]=a[i][0];		for(j=1;j<n;j++){dp[j][0] = MAX(dp[j-1][0],dp[j-1][1]);dp[j][1] = dp[j-1][0] + a[i][j];}		f[i] = MAX(dp[n-1][0],dp[n-1][1]);}dp[0][0] = 0;  dp[0][1] = f[0];for(j=1;j<m;j++){		dp[j][0] = MAX(dp[j-1][0],dp[j-1][1]);dp[j][1] = dp[j-1][0] + f[j];}				printf("%d\n",MAX(dp[m-1][0],dp[m-1][1]));}return 0;
}         

HDU 题目

Beans

Bean-eating is an interesting game, everyone owns an M*N matrix, which is filled with different qualities beans. Meantime, there is only one bean in any 1*1 grid. Now you want to eat the beans and collect the qualities, but everyone must obey by the following rules: if you eat the bean at the coordinate(x, y), you can’t eat the beans anyway at the coordinates listed (if exiting): (x, y-1), (x, y+1), and the both rows whose abscissas are x-1 and x+1.


Now, how much qualities can you eat and then get ?

  
4 6
11 0 7 5 13 9
78 4 81 6 22 4
1 40 9 34 16 10
11 22 0 33 39 6

  
242

改进代码：

#define N 200005
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
int MAX(int x,int y){return x>y?x:y;
}
int a[N],dp[N][2],f[N]; 
int main()
{int m,n,i,j,k,max;        while(scanf("%d%d",&m,&n)!=EOF){    for(i=0;i<m;i++) {for(j=0;j<n;j++)scanf("%d",&a[j]);                            dp[0][0]=0; dp[0][1]=a[0];    for(j=1;j<n;j++){dp[j][0] = MAX(dp[j-1][0],dp[j-1][1]);dp[j][1] = dp[j-1][0] + a[j];}        f[i] = MAX(dp[n-1][0],dp[n-1][1]);                                                        }dp[0][0] = 0;  dp[0][1] = f[0];for(j=1;j<m;j++){        dp[j][0] = MAX(dp[j-1][0],dp[j-1][1]);dp[j][1] = dp[j-1][0] + f[j];}    printf("%d\n",MAX(dp[m-1][0],dp[m-1][1]));}return 0;
} 

这篇关于NYOJ 题目17 单调递增最长子序列 （DP） hdu 题目2845 Bean的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！