本文主要是介绍【因果推断python】11_分组和虚拟变量回归2,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
虚拟变量回归
关键思想
虚拟变量回归
虚拟变量是我们编码为二进制列的分类变量。例如,假设您有一个希望包含在模型中的性别变量。该变量被编码为 3 个类别:男性、女性和其他性别。
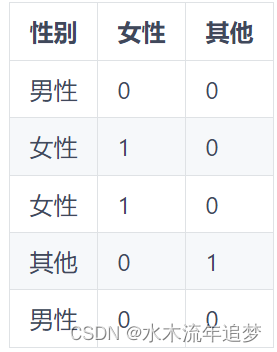
由于我们的模型只接受数值,我们需要将这个类别转换为数字。在线性回归中,我们为此使用了虚拟变量。我们将每个变量编码为 0/1 列,表示类别的存在。我们还将其中一个类别作为基本类别。这是必要的,因为最后一个类别是其他类别的线性组合。换句话说,如果有人向我们提供其他类别的信息,我们就可以知道最后一个类别。在我们的示例中,如果某人既不是女性也不是其他性别,我们可以推断该人的类别是男性。
在处理 A/B 测试时,我们已经处理了一种简单形式的虚拟回归。更一般地,当我们处理二元处理时,我们将其表示为虚拟变量。在这种情况下,该虚拟变量的回归系数是回归线中截距的增量,或处理和未处理之间的均值差异。
为了更具体地说明这一点,请考虑估计高中毕业(12年级毕业)对小时工资的影响的问题(让我们暂时忽略混杂因素)。在下面的代码中,我们创建了一个处理虚拟变量“T”,指示受教育年限是否大于 12。
wage = (pd.read_csv("./data/wage.csv").assign(hwage=lambda d: d["wage"] / d["hours"]).assign(T=lambda d: (d["educ"] > 12).astype(int)))wage[["hwage", "IQ", "T"]].head()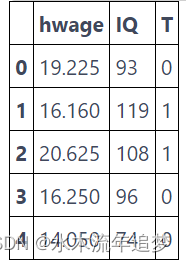
虚拟变量作为一种开关工作。 在我们的示例中,如果虚拟变量值为1,则预测值是截距加上虚拟变量对应的系数。 如果虚拟变量为值0,则预测值只是截距。
smf.ols('hwage ~ T', data=wage).fit().summary().tables[1]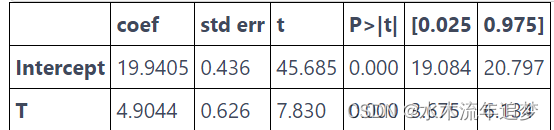
在这种情况下,当此人未完成 12 年级(虚拟变量为0)时,平均收入为 19.9。当他或她完成 12 年级(虚拟变量为1)时,预测值或平均收入为 24.8449 (19.9405 + 4.9044)。因此,虚拟系数捕捉了均值的差异,在我们的案例中为 4.9044。
用更正式的表述来讲,当因变量是二元变量时,就像干预指标的情况一样,回归完美地捕捉了 ATE。这是因为回归是条件期望函数 (CEF) E[Y|X] 的线性近似,在这种特殊情况下,CEF 是线性的。即,我们可以定义 和
,这导致以下 CEF
和 β 是随机数据的平均值或 ATE 的差异
如果我们使用额外的变量,虚拟变量系数将成为 条件 均值差异。例如,假设我们将 IQ 添加到之前的模型中。现在,虚拟系数告诉我们 12 年级 在保持 IQ 固定 的情况下应该期望增加多少。如果我们绘制预测图,我们将看到两条平行线。从一行跳到下一行表示我们完成高中后平均收入的预期数量。并且,这个差异效果是恒定的。即,无论您的智商如何,每个人都从高中毕业学历中有同样的受益。
m = smf.ols('hwage ~ T+IQ', data=wage).fit()
plt_df = wage.assign(y_hat = m.fittedvalues)plt.plot(plt_df.query("T==1")["IQ"], plt_df.query("T==1")["y_hat"], c="C1", label="T=1")
plt.plot(plt_df.query("T==0")["IQ"], plt_df.query("T==0")["y_hat"], c="C2", label="T=0")
plt.title(f"E[T=1|IQ] - E[T=0|IQ] = {round(m.params['T'], 2)}")
plt.ylabel("Wage")
plt.xlabel("IQ")
plt.legend();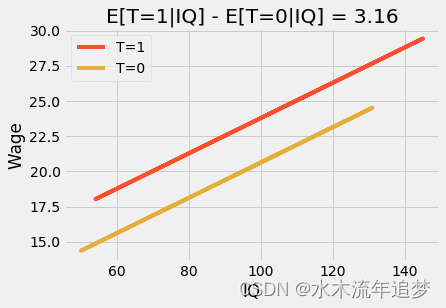
如果我们把这个模型放到一个方程中,我们就会明白为什么:
这里, 是均值的条件差,它是一个常数值,在我们的例子中是 3.16。我们可以通过添加交互项来使这个模型更加灵活。
事情变得有点复杂,所以让我们看看每个参数在这个模型中的含义。首先,截取 。这个坏男孩没有特别有趣的解释。这是治疗为零(此人未从 12 年级毕业)且 IQ 为零时的预期工资。由于我们不希望任何人的 IQ 为零(实际上……没关系),因此该参数不是很有意义。现在,当我们转向
时,我们遇到了类似的情况。这个参数是我们在完成 12 年级 当 IQ 为零时应该期望增加多少工资。再说一次,由于智商永远不会为零,因此它没有特别有趣的含义。现在,
更有趣一些。它告诉我们 IQ 增加了多少 未接受治疗的的工资。所以,在我们的例子中,它类似于 0.11。这意味着每增加 1 个 IQ 点,未完成 12 年级的人应该期望每小时增加 11 美分。最后,最有趣的参数是
。它告诉我们 IQ 对 12 年级毕业的影响有多大。在我们的例子中,这个参数是 0.024,这意味着对于每一个额外的 IQ 点,从 12 年级毕业会给 2 美分。这可能看起来不多,但比较一下 60IQ 和 140IQ 的人。第一个将获得 1.44 的工资增长(60 * 0.024),而智商为 140 的人从 12 年级毕业时将获得额外的 3.36 美元(60 * 0.024)。
用简单的建模术语来说,这个交互项允许治疗效果根据特征的级别(在这个例子中只有 IQ)而改变。结果是,如果我们绘制预测线,我们将看到它们不再平行,并且那些 12 年级 (T=1) 毕业的人在 IQ 上有更高的斜率,高智商比低智商受益更多。这有时被称为效果修改或异质治疗效果。
m = smf.ols('hwage ~ T*IQ', data=wage).fit()
plt_df = wage.assign(y_hat = m.fittedvalues)plt.plot(plt_df.query("T==1")["IQ"], plt_df.query("T==1")["y_hat"], c="C1", label="T=1")
plt.plot(plt_df.query("T==0")["IQ"], plt_df.query("T==0")["y_hat"], c="C2", label="T=0")
plt.title(f"E[T=1|IQ] - E[T=0|IQ] = {round(m.params['T'], 2)}")
plt.ylabel("Wage")
plt.xlabel("IQ")
plt.legend();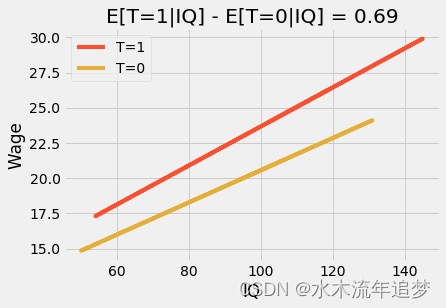
最后,让我们看看我们模型中的所有变量都是哑元的情况。 为此,我们将 IQ 离散为 4 个 bin,并将受教育年限视为一个类别。
wage_ed_bins = (wage.assign(IQ_bins = lambda d: pd.qcut(d["IQ"], q=4, labels=range(4)))[["hwage", "educ", "IQ_bins"]])wage_ed_bins.head()
plt.scatter(wage["educ"], wage["hwage"])
plt.plot(wage["educ"].sort_values(), model_dummy.predict(wage["educ"].sort_values()), c="C1")
plt.xlabel("Years of Education")
plt.ylabel("Hourly Wage");将教育视为一个类别,我们不再将教育的效果限制在单个参数上。 相反,我们允许每一年的教育都有自己独特的影响。 通过这样做,我们获得了灵活性,因为教育的效果不再是参数化的。 这个模型只是计算每一年教育的平均工资。
model_dummy = smf.ols('hwage ~ C(educ)', data=wage).fit()
model_dummy.summary().tables[1]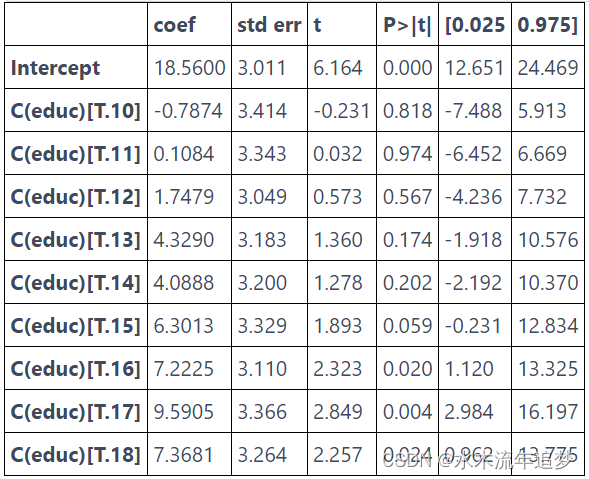
plt.scatter(wage["educ"], wage["hwage"])
plt.plot(wage["educ"].sort_values(), model_dummy.predict(wage["educ"].sort_values()), c="C1")
plt.xlabel("Years of Education")
plt.ylabel("Hourly Wage");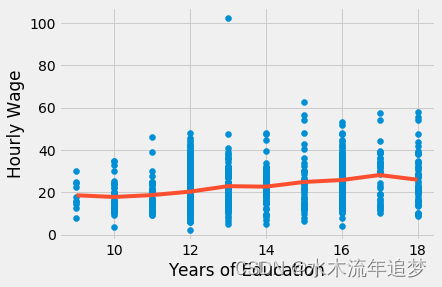
首先,请注意这如何消除关于教育如何影响工资的功能形式的任何假设。 我们不再需要担心对数函数的处理。 本质上,这个模型是完全非参数化的。 它所做的只是计算每一年教育的样本平均工资。 这可以在上图中看到,其中拟合线没有特定形式。 相反,是对每一年教育的样本均值进行插值。 我们还可以通过重构一个参数来看到这一点,例如对于具备17年教育年限水平的分组的参数。 对于这个模型,它是“9.5905”。 下面,我们可以看到基线教育年限水平 (9) 与 17 年教育年限水平的个人之间的差异
需要权衡的点是,当我们允许这种较大的灵活性时,我们会同步失去统计显著性。 请注意某些教育年限水平的 p 值有多大。
t1 = wage.query("educ==17")["hwage"]
t0 = wage.query("educ==9")["hwage"]
print("E[Y|T=9]:", t0.mean())
print("E[Y|T=17]-E[Y|T=9]:", t1.mean() - t0.mean())E[Y|T=9]: 18.56
E[Y|T=17]-E[Y|T=9]: 9.59047236235352如果我们在模型中包含更多的虚拟协变量,则教育参数成为对每个虚拟组影响的加权平均值:
并不是一成不变的,而是与该样本组中干预因子的方差,即
成正比。 由此自然而然产生的一个问题是,为什么不使用完整的非参数估计量,其中组权重是样本量? 这确实是一个有效的估计量,但它不是回归所做的。 通过使用干预因子的方差,回归将更多的权重放在干预在样本间变化很大的组上。 这是符合直觉的。 如果干预几乎是恒定的(比如 1 个人被干预而其他所有人都未被干预),则其样本大小无关紧要。 它不会提供有关干预效果的太多信息。
model_dummy_2 = smf.ols('hwage ~ C(educ) + C(IQ_bins)', data=wage_ed_bins).fit()
model_dummy_2.summary().tables[1]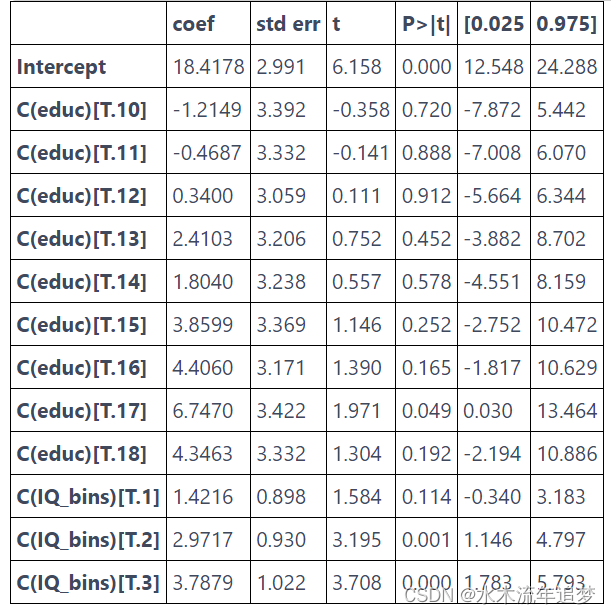
关键思想
我们通过查看某些数据点如何比其他数据点更重要来开始本节。 即,在估计线性模型时,应给予具有较大样本量和较低方差的样本更多的权重。 然后,我们研究了线性回归如何优雅地处理分组匿名数据,前提是我们在模型中使用了样本的权重。
之后,我们进而讨论了虚拟回归。 我们看到虚拟回归如何被设计为一个非参数模型,这类模型对干预因素如何影响结果的函数形式不做任何假设。 最后,我们探索了虚拟回归背后的直观含义。
这篇关于【因果推断python】11_分组和虚拟变量回归2的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





