Leecode---多维动态规划---不同路径 / 最小路径和 /最长公共子序列

本文主要是介绍Leecode---多维动态规划---不同路径 / 最小路径和 /最长公共子序列，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

动态规划—三部曲：
1、确定dp数组以及下标含义
dp[i][j]：表示从（0,0）出发，到（i,j）有dp[i][j]条不同的路径
2、确定递推公式
dp[i][j] = dp[i-1][j] + dp[i][j-1]
3、dp数组的初始化
如何初始化，dp[i][0]一定都是1，因为从（0,0）到（0,i）的路径只有一条，dp[0][j]同理：

for (int i = 0; i<m; i++) dp[i][0] = 1;
for (int j = 0; j<n; j++) dp[0][j] = 1;

知识点补充：二维容器vector< vector > 初始化方法解析：

vector<vector<int>> table(size1, vector<int>(size2, 0));

代码说明：声明一个名为table的容器，其元素为vector的容器。简单来说类似一个int型的二维数组。
这样，就得到了一个如下图所示的二维容器。

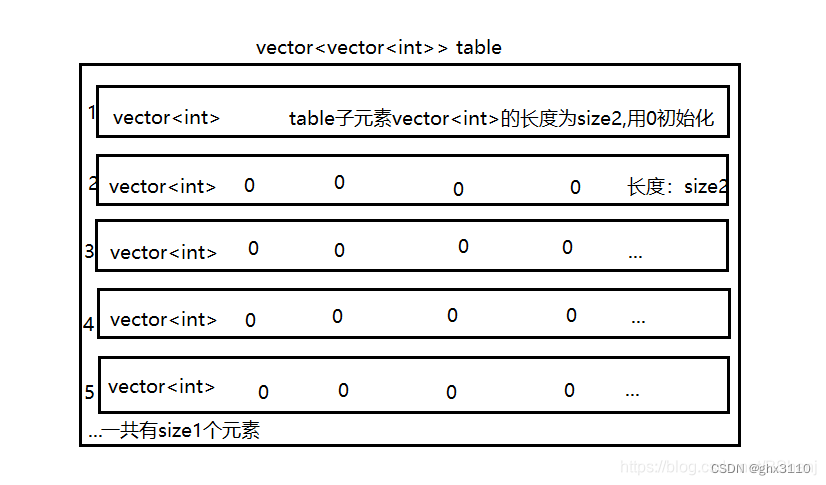
理解如下：

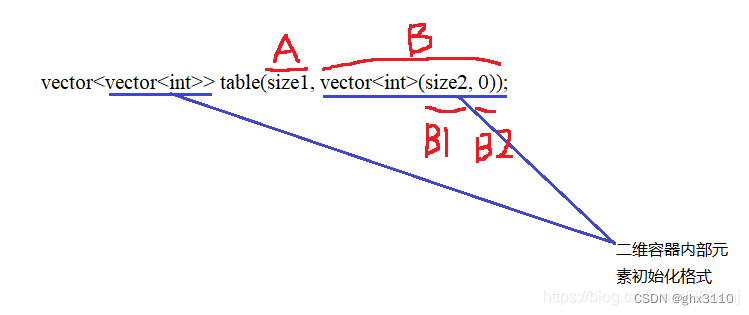
图中，将外围容器table的初始化参数分成了两部分A、B。
A: table外围容器的大小
B: table外围容器的内容，即size1个vector型的元素。
B1：内部容器的大小
B2：内部容器的内容

同理：三维容器初始化：
定义一个长宽高为2x3x5的立方体容器，每个元素为0：

//长宽高：2*3*5 vector<vector<vector<int>>> cube(5, vector<vector<int>>(3, vector<int>(2, 0)));

C++代码如下：

class Solution
{
public:int uniquePaths(int m, int n){// 声明一个名为dp的容器，其元素为vector的容器，类似一个int型的二维数组。vector<vector<int>> dp(m, vector<int>(n,0));for (int i = 0; i<m; i++) dp[i][0] = 1;for (int j = 0; j<n; j++) dp[0][j] = 1;for (int i = 1; i<m; i++){for(int j = 1; j<n; j++){dp[i][j] = dp[i-1][j] + dp[i][j-1];}}return dp[m-1][n-1];}
};

解法二、深搜（超时但同样容易理解）
机器人走过的路径可以抽象为一棵二叉树，而叶子节点就是终点！

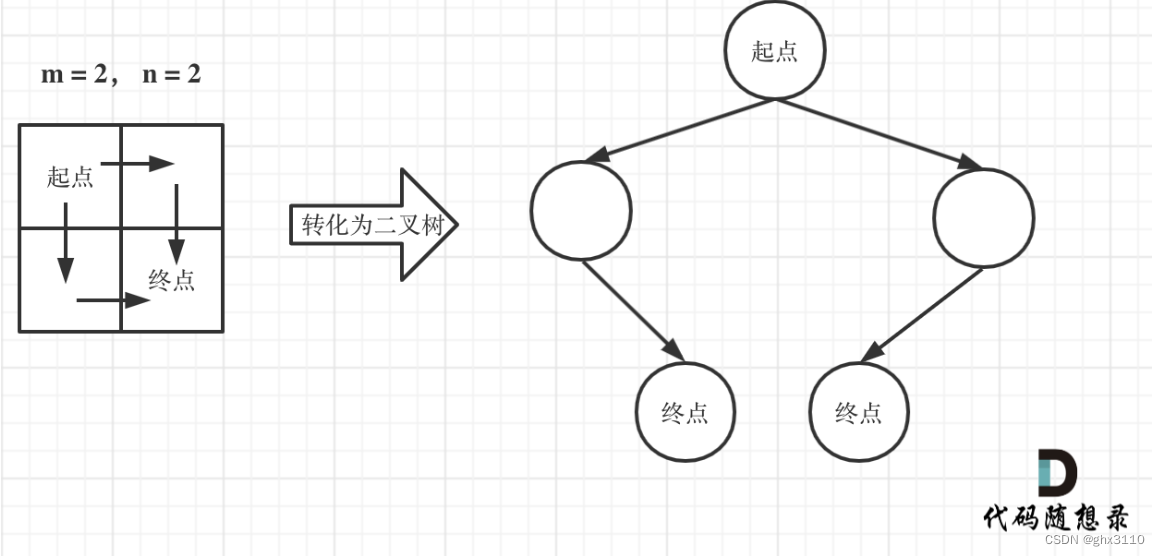
此时问题就可以转化为求二叉树叶子节点的个数，代码如下：

class Solution
{
private:int dfs(int i, int j, int m, int n){if(i>m || j>n) return 0;	//越界if(i == m && j == n) return 1;	// 找到一种方法，相当于找到了叶子节点return dfs(i+1, j, m, n) + dfs(i, j+1, m, n);}
public:int uniquePaths(int m, int n){return dfs(1,1,m,n);}
};

动态规划—三部曲：
1、确定dp数组以及下标含义
dp(i,j)：表示从（0,0）出发，到（i,j）的最小路径和
2、确定递推公式（转移方程）
左位置和上位置的最短路径和的最小值，加上当前位置的值：
dp(i,j) = min{dp(i-1,j), dp(i,j-1)} + arr[i][j]
3、dp数组的初始化
最左一列和第一行的所有位置都必须作为初始值，防止递推越界。
dp(0,j) = dp(0, j-1) + arr[0][j]
dp(i,0) = dp(i-1, 0) + arr[i][0]
返回值：返回数组右下角的值dp(m-1, n-1)

class Solution
{
public:int minPathSum(vector<vector<int>>& grid){int row = grid.size();int col = grid[0].size();// 初始化for(int i = 1; i<row; i++)grid[i][0] += grid[i-1][0];for(int j = 1; j<col; j++)grid[0][j] += grid[0][j-1];// dp 过程for(int i = 1; i<row; i++){for(int j = 1; j<col; j++){grid[i][j] += min(grid[i-1][j], grid[i][j-1]); }}return grid[row-1][col-1];}
};

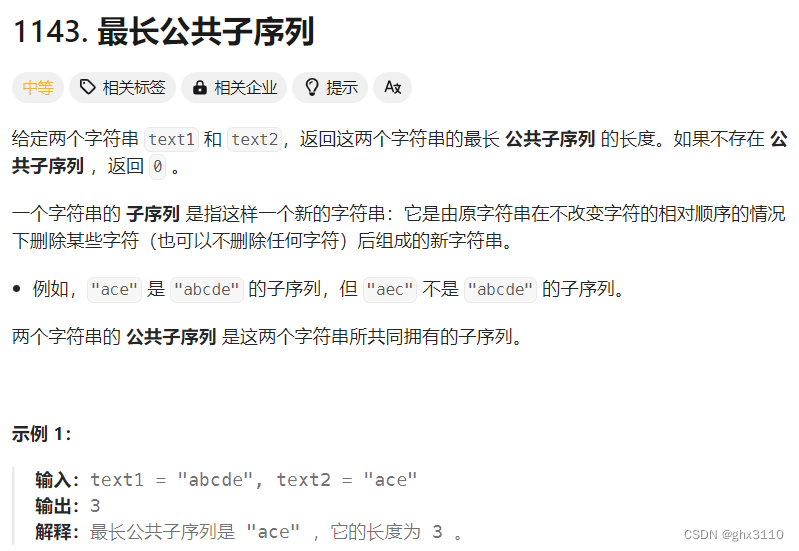
动态规划—三部曲：
1、确定字符串 f 及下标含义
定义 f[i][j] 表示字符串 text1 的 [1][i] 区间和字符串 text2 的 [1][j] 区间的最长公共子序列长度（下标从 1 开始）
2、初始化：
f[i][0] = f[0][j] = 0,（0 <= i <= n, 0 <= j <= m）
空字符串与有长度的字符串的最长公共子序列长度为0。
3、状态转移方程
① text1[i] == text2[j]，即两字符串最后一位相等，此时问题转化为text1的[1, i-1]区间和字符串text2的[1, j-1] 区间的最长公共子序列长度再加一，即：
f[i][j] = f[i-1][j-1] + 1 （下标从1开始）
② text1[i] != text2[j], 即两字符串的最后一位不相等，此时 f[i][j] 会继承 f[i-1][j] 与 f[i][j-1] 中的较大值，即：
f[i][j] = max(f[i-1][j], f[i][j-1]) 。（下标从1开始）

为什么下标从1开始：
由状态转移方程f[i][j] = max(f[i-1][j], f[i][j-1])，当从1开始时，代码中不用对下标越界问题做额外判断。题目给的是从0开始，因此判断条件往前错一位，使用 text1[i-1] 和 text2[j-1] 判断。

class Solution
{
public:int longestCommonSubsequence(string text1, string text2){int n = text1.size(), m = text2.size();// 初始化if(m==0 && n==0) return 0;// 初始化二维容器vector<vector<int>> f(n+1, vector<int>(m+1, 0));for(int i = 1; i<=n; i++){for(int j = 1;j<=m; j++){// 状态转移矩阵if(text1[i-1] == text2[j-1]){f[i][j] = f[i-1][j-1] + 1;}else{f[i][j] = max(f[i-1][j],f[i][j-1]);}}}return f[n][m];}
};

这篇关于Leecode---多维动态规划---不同路径 / 最小路径和 /最长公共子序列的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---