本文主要是介绍简单的基于小波分解和独立分量分析的脑电信号降噪(Python),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
脑电信号是一种典型的非平稳随机信号且存在一定的非高斯性和非线性。传统的分析处理方法是将脑电信号近似看做线性、准平稳、高斯分布的随机信号,这使得分析结果往往不能令人满意,实用性较差。现代的小波变换方法和独立分量分析方法的提出为有效地分析脑电信号提供了新的途径。由于所要提取的特征波频率不精确并受到噪声的影响,如果单独应用小波提取出的特征信号往往特征不够明显。独立分量分析是根据信号的多元统计特性进行分析处理,可以将多道混合信号进行独立分离。考虑到所要提取的特征波就是混合脑电信号中的一个独立分量,应用独立分量分析在一定程度上可以分离出特征波。
鉴于此,采用简单的小波分解和独立分量分析对脑电信号降噪,完整代码如下:
import numpy as np
import matplotlib.pyplot as plt
import pyedflib
# import sklearn.linear_model as slm
from sklearn import metrics
from statsmodels.tsa.ar_model import AutoReg
# import scipy
# import scipy.signal as signal
from sklearn.decomposition import FastICA
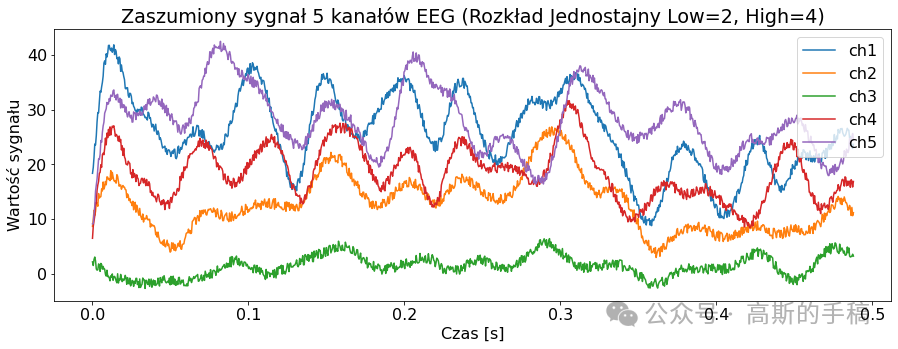
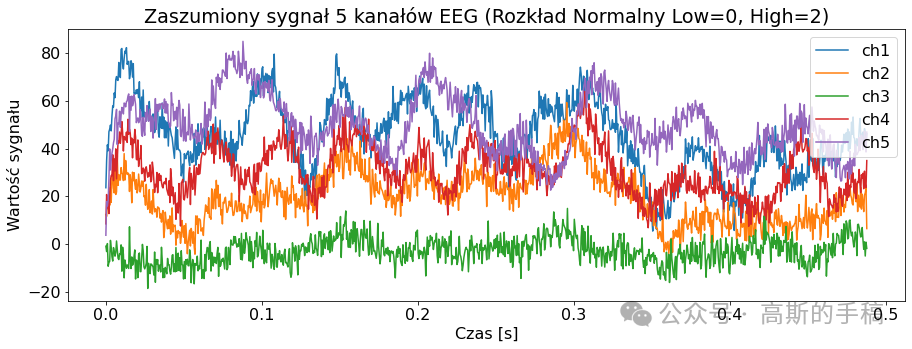
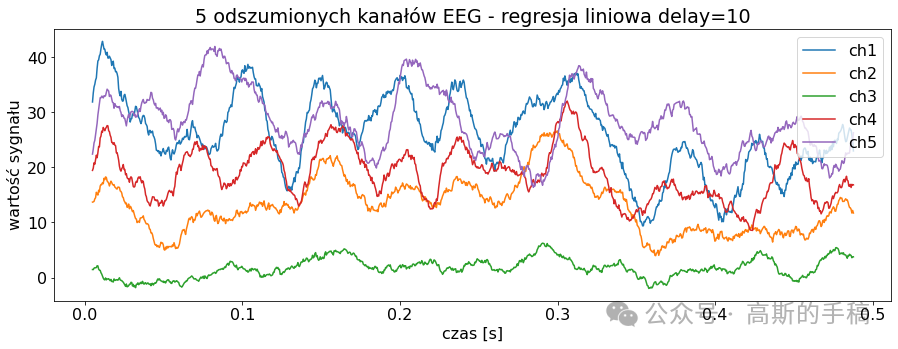
import pywtclass EEGSignalProcessing:def __init__(self) -> None:passdef read_signal(filename, number_of_samples = None, offset = 0):file = pyedflib.EdfReader(filename)if number_of_samples is None:number_of_samples = file.getNSamples()[0]number_of_signals = file.signals_in_filesignal = np.zeros((number_of_signals, number_of_samples))for i in range(number_of_signals):signal[i, :] = file.readSignal(i)[offset:offset + number_of_samples]file.close()return signaldef plot_signal(data, sampling_frequency, title, number_of_channels = None, channel_labels = None, yaxis_label = None, xaxis_label = None): plt.rcParams['font.size'] = '16'fig = plt.figure()ax = fig.add_subplot(1,1,1)lenght = len(data)if number_of_channels is None:number_of_channels_useful = range(0, lenght)else:if isinstance(number_of_channels, str):number_of_channels_useful = range(0, lenght-1)else:number_of_channels_useful = number_of_channelsfor channel in number_of_channels_useful:if channel_labels is None:label = 'ch' + str(channel + 1)else:label = channel_labels[channel]limit = data[channel, :].sizex_values = [num/sampling_frequency for num in range(0, limit)]ax.plot(x_values, data[channel, :], label = label)fig.set_size_inches(15,5)plt.title(title)plt.legend()if yaxis_label is not None:plt.ylabel(yaxis_label)if xaxis_label is not None:plt.xlabel(xaxis_label)plt.show(block = True)def channel_desynchronize(data_1d, delay, value = 0):number_of_samples = len(data_1d)if delay > 0:for i in range(number_of_samples - 1, delay - 1, -1):data_1d[i] = data_1d[i - delay]for i in range(0, delay):data_1d[i] = valueif delay < 0:delay = -delayfor i in range(0, number_of_samples - delay):data_1d[i] = data_1d[i + delay]for i in range(number_of_samples - delay, number_of_samples):data_1d[i] = value def all_channels_desynchronize(data, delay, value = 0):for i in range(0, len(data)):EEGSignalProcessing.channel_desynchronize(data[i], delay, value) class NoiseReduction:def autoregression(data, delay):signals_number = len(data)samples_number = len(data[0])output = np.zeros((signals_number, samples_number))for i in range(0, signals_number):model = AutoReg(data[i], lags=delay)model_fit = model.fit()predictions = model_fit.predict(start=0, end=samples_number-1, dynamic=False)output[i, :samples_number] = predictionsreturn outputdef wavelet(linear_array):name = 'bior3.1'# Create wavelet object and define parameterswav = pywt.Wavelet(name)max_level = pywt.dwt_max_level(len(linear_array) + 1, wav.dec_len)# print("Maximum level is " + str(max_level))threshold = 0.04 # Threshold for filtering# Decompose into wavelet components, to the level selected:coeffs = pywt.wavedec(linear_array, name, level=5)plt.figure()for i in range(1, len(coeffs)):plt.subplot(max_level, 1, i)plt.plot(coeffs[i])coeffs[i] = pywt.threshold(coeffs[i], threshold * max(coeffs[i]))plt.plot(coeffs[i])plt.show()datarec = pywt.waverec(coeffs, name)return np.array(datarec)def wavelet_all_channels(data):output = []for c in data:output.append(EEGSignalProcessing.NoiseReduction.wavelet(c))return np.stack(output)def ica(data, mask=None):# maska do wyboru składowychreduce_level = [True, True, True, True, True, True, True, True, True]reduce_level[7] = Falseif mask is not None:reduce_level = masksigT = data.Tn = data.shape[0]# obliczanie ICAica = FastICA(n_components=n)sig_ica = ica.fit_transform(sigT)# Macierz mmieszaniaA_ica = ica.mixing_# Przycięcie macierzy mieszającej, aby odrzucić najmniej znaczące wartościA_ica_reduced = A_icasig_ica = sig_ica[:, reduce_level]X_reduced = np.dot(sig_ica, A_ica_reduced.T[reduce_level, :]) + ica.mean_ica_reconstruct = X_reduced.Treturn ica_reconstructclass Noise:def add_uniform_noise(data, low, high, seed=None):signals_number = len(data)samples_number = len(data[0])output = np.zeros((signals_number, samples_number))if seed is not None:np.random.seed(seed)for i in range(signals_number):if isinstance(low, str):if low == "min_value":low = min(data[i])if isinstance(high, str):if high == "max_value":high = max(data[i])noise = np.random.uniform(low, high, samples_number)output[i] = data[i] + noisereturn outputdef add_normal_noise(data, mean, std, amplitude=1, seed=None):signals_number = len(data)samples_number = len(data[0])output = np.zeros((signals_number, samples_number))if seed is not None:np.random.seed(seed)for i in range(signals_number):noise = np.random.normal(mean, std, samples_number)output[i] = data[i] + noisereturn amplitude*outputdef add_triangular_noise(data, left, peak, right, seed=None):signals_number = len(data)samples_number = len(data[0])output = np.zeros((signals_number, samples_number))if seed is not None:np.random.seed(seed)for i in range(signals_number):noise = np.random.triangular(left, peak, right, samples_number)output[i] = data[i] + noisereturn outputclass Metrics:def __init__(self) -> None:passdef evaluate_signal(signal, prediction, cut_left=100, cut_right=100):signal_cut = signal[cut_left:-cut_right]predicted_cut = prediction[cut_left:-cut_right]# metryki z sklearnmae = metrics.mean_absolute_error(signal_cut, predicted_cut)mse = metrics.mean_squared_error(signal_cut, predicted_cut)# wyświetlanieprint('MAE z biblioteki sklearn: {}'.format(round(mae, 2)))print('MSE z biblioteki sklearn: {}'.format(round(mse, 2)))def differantial(sigA, sigB, cutleft=100, cutright=100):differential = sigA[:,cutleft:-cutright] - sigB[:,cutleft:-cutright]return differentialdef main():channels_to_plot = [0,1,2,3,4]# signal = EEGSignalProcessing.read_signal(filename = "Subject00_2.edf", number_of_samples=1000)# signal = EEGSignalProcessing.read_signal(filename = "Subject00_1.edf", number_of_samples=1000)signal = EEGSignalProcessing.read_signal(filename = "rsvp_10Hz_08b.edf", number_of_samples=1000)EEGSignalProcessing.plot_signal(signal,sampling_frequency= 2048, title = "Orginalne sygnały EEG", number_of_channels = channels_to_plot,yaxis_label='Wartosc sygnalu', xaxis_label='Czas [s]')low = 2high = 4sig_noise_uniform = EEGSignalProcessing.Noise.add_uniform_noise(signal, low=low, high=high, seed=100)EEGSignalProcessing.plot_signal(sig_noise_uniform, title="Zaszumiony sygnał 5 kanałów EEG (Rozkład Jednostajny Low={}, High={})".format(low, high), sampling_frequency=2048, number_of_channels=channels_to_plot, yaxis_label='Wartość sygnału', xaxis_label='Czas [s]')mean = 0std = 2ampl = 2sig_noise_normal = EEGSignalProcessing.Noise.add_normal_noise(signal, mean=mean, std=std, amplitude=ampl, seed=100)EEGSignalProcessing.plot_signal(sig_noise_normal, title="Zaszumiony sygnał 5 kanałów EEG (Rozkład Normalny Low={}, High={})".format(mean, std), sampling_frequency=2048, number_of_channels=channels_to_plot, yaxis_label='Wartość sygnału', xaxis_label='Czas [s]')sig_n3_left = 0sig_n3_peak = 4sig_n3_right = 6sig_noise_triangular = EEGSignalProcessing.Noise.add_triangular_noise(signal, left=sig_n3_left, peak=sig_n3_peak, right=sig_n3_right, seed=100)EEGSignalProcessing.plot_signal(sig_noise_triangular, title="Zaszumiony sygnał 5 kanałów EEG (Rozkład Trójkątny Left={}, Peak={}, High={})".format(sig_n3_left, sig_n3_peak, sig_n3_right), sampling_frequency=2048, number_of_channels=channels_to_plot, yaxis_label='Wartość sygnału', xaxis_label='Czas [s]')# Odszumianie sygnałów# AutoregresjaAR_lag = 10signal_autoregresion = EEGSignalProcessing.NoiseReduction.autoregression(sig_noise_triangular, delay = AR_lag)EEGSignalProcessing.plot_signal(signal_autoregresion,title="5 odszumionych kanałów EEG - regresja liniowa delay={}".format(AR_lag), sampling_frequency=2048, number_of_channels=channels_to_plot,yaxis_label='wartość sygnału', xaxis_label='czas [s]')# Waveletsignal_wavelet = EEGSignalProcessing.NoiseReduction.wavelet_all_channels(sig_noise_triangular)EEGSignalProcessing.plot_signal(signal_wavelet,title="5 odszumionych kanałów EEG - Wavelet", sampling_frequency=2048, number_of_channels=channels_to_plot,yaxis_label='wartość sygnału', xaxis_label='czas [s]')# ICAsignal_ICA = EEGSignalProcessing.NoiseReduction.ica(sig_noise_triangular)EEGSignalProcessing.plot_signal(signal_ICA,title="5 odszumionych kanałów EEG - ICA", sampling_frequency=2048, number_of_channels=channels_to_plot,yaxis_label='wartość sygnału', xaxis_label='czas [s]')# Metrykich = 4noise_signal = sig_noise_normalprint('\nORYGINALNY')Metrics.evaluate_signal(signal[ch], signal[ch])print('\nNIEODSZUMIONY, dodano szum rozkład normalny')Metrics.evaluate_signal(signal[ch], noise_signal[ch])print('\nODSZUMIONY, najpierw dodano szum rozkład normalny, potem autoregresja')Metrics.evaluate_signal(signal[ch], signal_autoregresion[ch])print('\nODSZUMIONY, najpierw dodano szum rozkład normalny, potem ICA')Metrics.evaluate_signal(signal[ch], signal_ICA[ch])print('\nODSZUMIONY, najpierw dodano szum rozkład normalny, potem wavelet')Metrics.evaluate_signal(signal[ch], signal_wavelet[ch])# Sygnał różnicowydifferential_noise = Metrics.differantial(sig_noise_normal, signal)differential_AR = Metrics.differantial(signal_autoregresion, signal)differential_ICA = Metrics.differantial(signal_ICA, signal)differential_Wavelet = Metrics.differantial(signal_wavelet, signal)EEGSignalProcessing.plot_signal(differential_noise, title="Sygnał różnicowy, zaszumiony-orginalny",sampling_frequency=2048, number_of_channels=[ch], yaxis_label="Wartość sygnału",xaxis_label="Czas [s]")EEGSignalProcessing.plot_signal(differential_AR, title="Sygnał różnicowy, AR-orginalny",sampling_frequency=2048, number_of_channels=[ch], yaxis_label="Wartość sygnału",xaxis_label="Czas [s]")EEGSignalProcessing.plot_signal(differential_ICA, title="Sygnał różnicowy, ICA-orginalny",sampling_frequency=2048, number_of_channels=[ch], yaxis_label="Wartość sygnału",xaxis_label="Czas [s]")EEGSignalProcessing.plot_signal(differential_Wavelet, title="Sygnał różnicowy, wavelet-orginalny",sampling_frequency=2048, number_of_channels=[ch], yaxis_label="Wartość sygnału",xaxis_label="Czas [s]")
完整代码:https://mbd.pub/o/bread/mbd-ZZWYlJlpif __name__ == '__main__':main()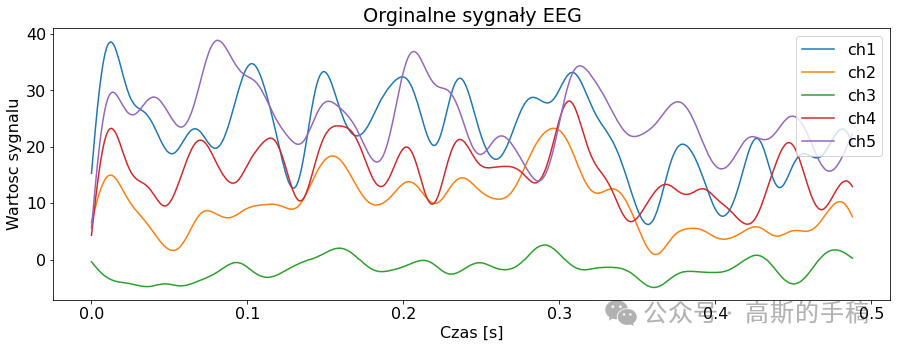
工学博士,担任《Mechanical System and Signal Processing》《中国电机工程学报》《控制与决策》等期刊审稿专家,擅长领域:现代信号处理,机器学习,深度学习,数字孪生,时间序列分析,设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。
这篇关于简单的基于小波分解和独立分量分析的脑电信号降噪(Python)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



