桶形畸变和枕形畸变

本文主要是介绍桶形畸变和枕形畸变，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

桶形畸变和枕形畸变是两种常见的光学畸变现象，主要发生在使用广角镜头或远摄镜头拍摄时。这些畸变是因为镜头的光学特性不能完美地将光线汇聚到一个共同的焦点上，导致图像的不同部分在形状上发生扭曲。下面分别对这两种畸变进行详细描述：

桶形畸变（Barrel Distortion）

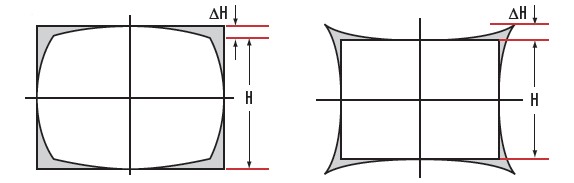
定义： 桶形畸变，也称为鼓形畸变，是指图像的边缘部分向外弯曲，中心区域则相对正常或稍微凸起，整体形状类似于一个木桶的横截面。这种畸变使得直线看起来在画面的边缘处弯曲，形成一种“弓形”效果。

原因： 桶形畸变通常发生在广角镜头中，尤其是在镜头设计中为了获得更宽的视角而做出的某些光学妥协时。它是因为镜头边缘的光线相较于中心光线以更大的角度进入镜头，但未能精确汇聚到与中心光线相同的焦平面上，从而导致了边缘的放大率高于中心区域。

影响： 这种畸变在拍摄具有直线特征的场景时尤为明显，如建筑摄影、风景摄影中的水平线和垂直线会显得弯曲。

枕形畸变（Pincushion Distortion）

定义： 与桶形畸变相反，枕形畸变使得图像的边缘向内弯曲，而中心区域则显得扁平或凹陷，整体形态类似一个被压扁的枕头。这意味着原本应为直线的物体在图像的边缘区域会呈现出向内弯折的“V”字形。

原因： 枕形畸变多见于远摄镜头，尤其是长焦距镜头。这是因为远摄镜头需要更复杂的光学设计来聚焦远处的光线，这可能导致中心区域的光线汇聚位置比边缘光线更靠前，从而产生这种畸变。

影响： 枕形畸变在拍摄细节丰富、要求高精度对齐的场景时较为显著，比如产品摄影、微距摄影等，其中直线的准确再现尤为重要。

图像示例：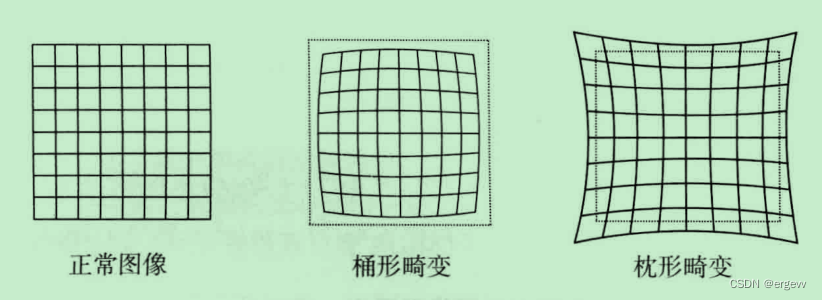

去畸变公式：

$$x_{distorted}=x(1+k_1\ast r^2+k_2\ast r^4+k_3\ast r^6)+2\ast p_1\ast x\ast y+p_2\ast (r^2+2\ast x^2)$$
$$y_{distorted}=y(1+k_1\ast r^2+k_2\ast r^4+k_3\ast r^6)+p_1\ast (r^2+2\ast y^2)+2\ast p_2\ast x\ast y$$

这个公式是一个用于描述图像畸变的数学模型，通常用于计算由镜头产生的桶形畸变和枕形畸变。该模型基于多项式展开，可以用来纠正图像中的几何失真。

在这个公式中，有以下几个关键参数：

• x 和 y 是原始未畸变图像坐标系下的像素坐标。
• x_distorted 和 y_distorted 是经过畸变后的图像坐标系下的像素坐标。
• r² = x² + y² 表示像素点到图像中心的距离平方。
• k_1, k_2, and k_3 是表示畸变程度的系数，它们决定了畸变的程度和类型。这些系数可以通过实际测量和校准得到。
• p_1 和 p_2 是表示径向畸变和切向畸变的额外系数。

1. 径向畸变 (Radial Distortion):
   • x_distorted = x(1 + k_1 r^2 + k_2 r^4 + k_3 r^6)
   • y_distorted = y(1 + k_1 r^2 + k_2 r^4 + k_3 r^6)

这部分描述的是由于透镜曲率不均匀造成的径向畸变。随着距离透镜中心越远，畸变程度越大。k_1, k_2, and k_3 分别对应第一阶、第二阶和第三阶径向畸变系数。

2. 切向畸变 (Tangential Distortion):
   • x_distorted += 2 p_1 xy
   • y_distorted += p_1(r^2 + 2y^2) + 2 p_2 xy

这部分描述的是由于透镜平面与成像传感器平面不平行造成的切向畸变。p_1 和 p_2 参数分别对应两个不同的切向畸变项。

通过调整这些参数，可以计算出每个像素的实际位置，并将其映射回正确的空间位置，从而实现对图像畸变的矫正。在实际应用中，这些参数通常是通过对一组已知参考点进行校准得出的。

这篇关于桶形畸变和枕形畸变的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---