Lesson6--排序(初级数据结构完结篇)

本文主要是介绍Lesson6--排序(初级数据结构完结篇)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1.排序的概念及其运用

1.1排序的概念  

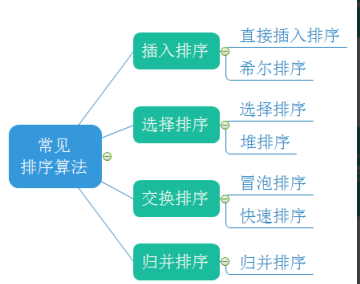
 1.3 常见的排序算法

// 排序实现的接口
// 插入排序
void InsertSort(int* a, int n);
// 希尔排序
、void ShellSort(int* a, int n);
// 选择排序
void SelectSort(int* a, int n);
// 堆排序
void AdjustDwon(int* a, int n, int root);
void HeapSort(int* a, int n);
// 冒泡排序
void BubbleSort(int* a, int n)
// 快速排序递归实现
// 快速排序hoare版本
int PartSort1(int* a, int left, int right);
// 快速排序挖坑法
int PartSort2(int* a, int left, int right);
// 快速排序前后指针法
int PartSort3(int* a, int left, int right);
void QuickSort(int* a, int left, int right);
// 快速排序 非递归实现
void QuickSortNonR(int* a, int left, int right)
// 归并排序递归实现
void MergeSort(int* a, int n)
// 归并排序非递归实现
void MergeSortNonR(int* a, int n)
// 计数排序
void CountSort(int* a, int n)
// 测试排序的性能对比
void TestOP()
{srand(time(0));const int N = 100000;int* a1 = (int*)malloc(sizeof(int)*N);int* a2 = (int*)malloc(sizeof(int)*N);int* a3 = (int*)malloc(sizeof(int)*N);int* a4 = (int*)malloc(sizeof(int)*N);int* a5 = (int*)malloc(sizeof(int)*N);int* a6 = (int*)malloc(sizeof(int)*N);for (int i = 0; i < N; ++i){a1[i] = rand();a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];a5[i] = a1[i];a6[i] = a1[i];
}int begin1 = clock();InsertSort(a1, N);int end1 = clock();int begin2 = clock();ShellSort(a2, N);int end2 = clock();int begin3 = clock();SelectSort(a3, N);int end3 = clock();int begin4 = clock();HeapSort(a4, N);int end4 = clock();int begin5 = clock();QuickSort(a5, 0, N-1);int end5 = clock();int begin6 = clock();MergeSort(a6, N);int end6 = clock();printf("InsertSort:%d\n", end1 - begin1);printf("ShellSort:%d\n", end2 - begin2);printf("SelectSort:%d\n", end3 - begin3);printf("HeapSort:%d\n", end4 - begin4);printf("QuickSort:%d\n", end5 - begin5);printf("MergeSort:%d\n", end6 - begin6);free(a1);free(a2);free(a3);free(a4);free(a5);free(a6);
}

 排序OJ(可使用各种排序跑这个OJ)912. 排序数组 - 力扣（LeetCode）

2.常见排序算法的实现 

2.1 插入排序

2.1.1基本思想：

直接插入排序是一种简单的插入排序法，其基本思想是：

 

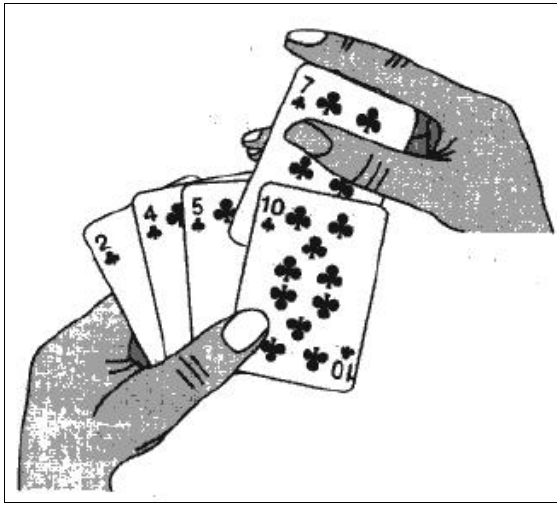
2.1.2直接插入排序： 

 

代码实现：

void InsertSort(int* arr, int length)
{for (int i = 0; i < length-1; i++){int end=i;int temp = arr[end + 1];while (end >= 0){if (temp < arr[end]){arr[end+1] = arr[end];}else{break;}end--;}arr[end + 1] = temp;}}

2.1.3希尔排序

希尔排序法又称缩小增量法。希尔排序法的基本思想是：先选定一个整数，把待排序文件中所有记录分成个 组，所有距离为的记录分在同一组内，并对每一组内的记录进行排序。然后，取，重复上述分组和排序的工 作。当到达gap=1时，所有记录在统一组内排好序

 

时间复杂度可以即一个结论大概是：N^1.3 

 

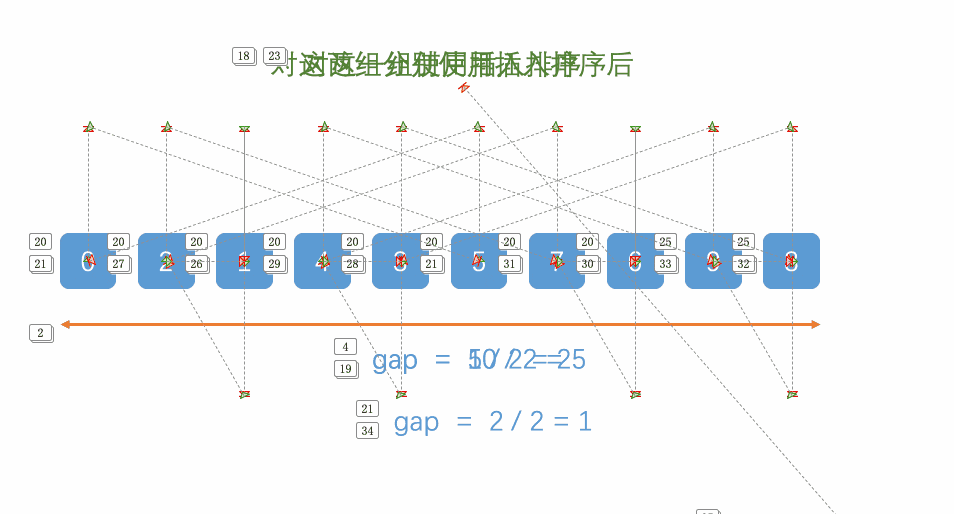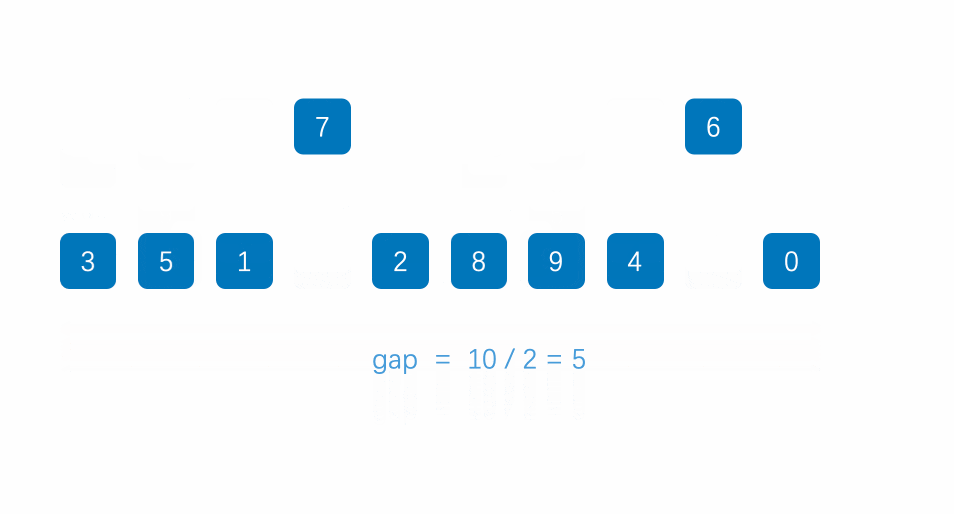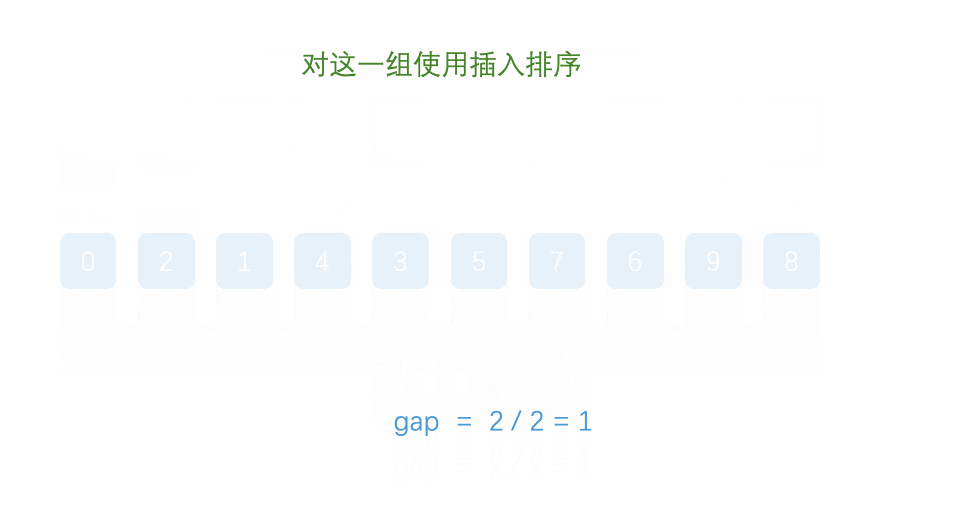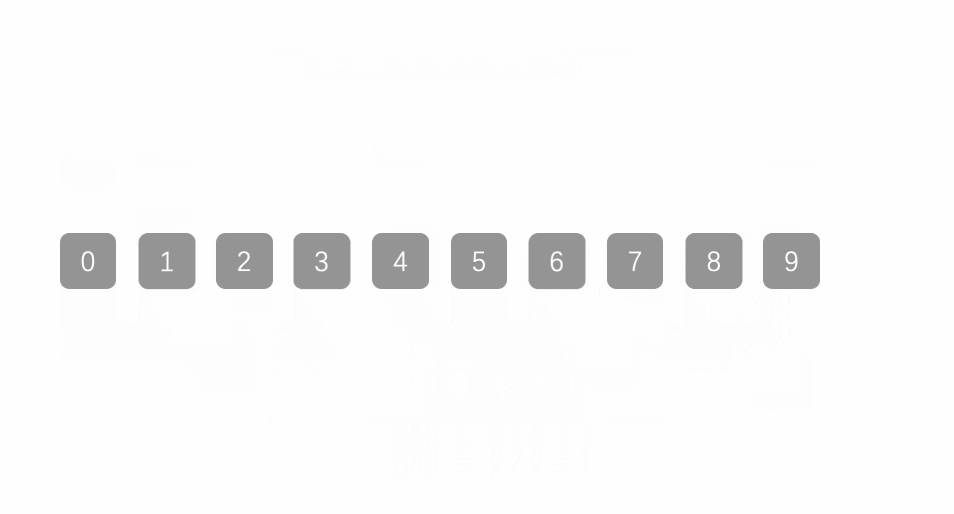
代码实现：

 

void SellSort(int* arr, int length)
{int gap = length;while (gap>1){gap = gap / 3 + 1;for (int  i = 0; i < length-gap; i++){int end = i;int temp = arr[end + gap];while (end>=0){if (temp < arr[end]){arr[end + gap] = arr[end];end = end - gap;}else{break;}}arr[end + gap] = temp;}}
}

2.2冒泡排序

基本思路：
左边大于右边交换一趟排下来最大的在右边

 

冒泡排序的特点包括：
1. 冒泡排序适合处理元素集合越接近有序的情况，时间效率会更高。
2. 冒泡排序的时间复杂度为O(N^2)，性能较差，不适用于处理大规模数据的排序。
3. 冒泡排序是一种稳定的排序算法，相同元素的相对位置不会发生改变。
4. 冒泡排序的空间复杂度为O(N)，是一种原地排序算法。
5. 冒泡排序是一种交换排序算法，通过不断比较相邻的元素并交换位置来达到排序的目的。
 

代码实现：

void BubbleSort(int* arr, int length)
{for (int i = 0; i < length-1; i++){int flag = 0;for (int j = 0; j < length-i-1; j++){if (arr[j] > arr[j + 1]) {Swap(&arr[j], &arr[j + 1]);flag = 1;}}if (flag == 0){break;}}
}

2.3堆排序

堆排序是一种基于二叉堆数据结构的排序算法，其基本思路如下：

1. 构建最大堆或最小堆：将待排序的数组视作一个完全二叉树，并且通过调整父节点与子节点的关系，使得每个父节点的值都大于或小于其子节点的值，即构建最大堆或最小堆。

2. 将堆顶元素与最后一个元素交换：将根节点（最大值或最小值）与最后一个元素交换位置。

3. 调整堆结构：交换元素后，调整堆结构，使其重新满足最大堆或最小堆的性质。

4. 重复步骤2和3：重复进行上述步骤，直到所有元素都被交换到对应的位置，即完成排序。

堆排序的时间复杂度为O(nlogn)，其中n为待排序数组的长度。堆排序是一种原地排序算法，不需要额外的空间，但性能较差且不稳定。

 

代码实现： 

void AdjustDown(int* arr,int length, int parent)
{int child = parent * 2 + 1;while (child<length){if (child+1<length && arr[child + 1] > arr[child]){child++;}if (arr[child] > arr[parent]){Swap(&arr[child], &arr[parent]);parent = child;child = child * 2 + 1;}else{break; }}
}
void HeapSort(int* arr, int length)
{for (int i = (length-1-1)/2; i >= 0; i--){AdjustDown(arr, length, i);}int end = length - 1;while (end > 0){Swap(&arr[0], &arr[end]);AdjustDown(arr, end, 0);end--;}
}

 

这篇关于Lesson6--排序(初级数据结构完结篇)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---