本文主要是介绍量变与质变——“学而不思则罔,思而不学则殆”——圆锥世界,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
质量互变规律是唯物辩证法的基本规律之二。它揭示了事物发展量变和质变的两种状态,以及由于事物内部矛盾所决定的由量变到质变,再到新的量变的发展过程。这一规律,提供了事物发展是质变和量变的统一、连续性和阶段性的统一的观察事物的原则和方法。[1]
摘自《马克思哲学原理》
问题
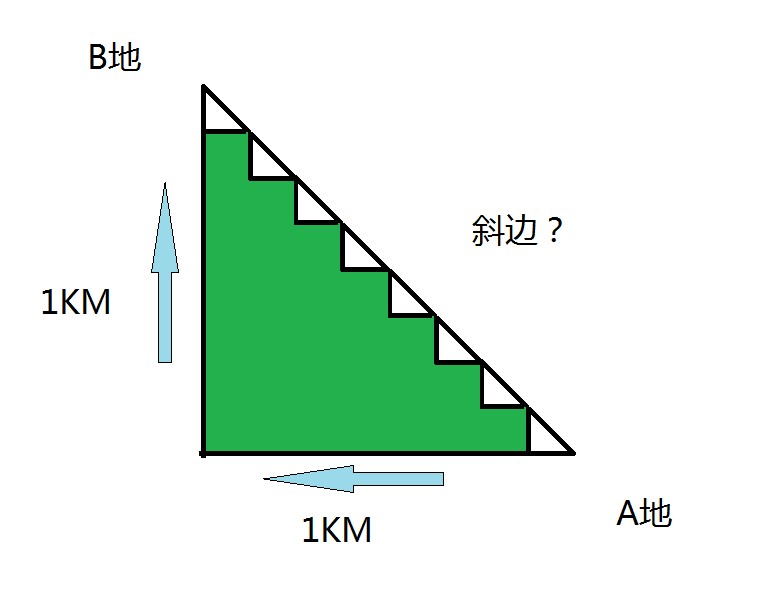
有天回家的路上经过一个公园,很自然的走了斜线。突然想到这个问题。
为什么从A地到B地斜边的距离会比直角边短?
相信只要数学不太差的同学都会秒解斜边长,但是问题来了,如果将斜边划分成小的三角形,小三角形的同方向直角边的和正好等于原始三角形的直角边。小三角形斜边和等于大三角形斜边。
似乎可以这么说,因为小三角形的斜边比直角边短,所以大三角形的斜边也比直角边短。虽然挺有道理,但是这样分下去,即使分到人类知觉的精度外,似乎问题并没有解决。反倒陷入了循环。
背景知识
高等数学最开始讲的是极限,通过“ε——N” 定义了极限,又在极限的基础上导出了微积的思想。
定义:
设{xn}为一无穷实数数列的集合。如果存在实数a,对于任意正数ε (不论它多么小),总存在正整数N,使得当n>N时,均有 不等式成立,那么就称常数a是数列{xn} 的极限,或称数列{xn} 收敛于a。
通俗地讲,微积分是一种数学思想,“无限细分”就是微分,“无限求和”就是积分。
无限==极限,极限的思想是微积分的基础,它是用一种运动的角度看待问题。
微积分学的建立,对现代科学产生了巨大的影响。如果仅仅是数学,那么也就只是数学家的事了。马克思把研究数学作为丰富唯物辩证法的一个源泉。通过自己对数学的多年钻研,终于在高等数学中,他找到了最符合逻辑的同时又是形式最简单的辩证运动。
分析
回到问题“量变与质变”,人类用循环无限的理论近似的表达了人类直觉之外的世界,真正的捷径不在于不断缩小微分的量,因为即使无限的缩小,对于加速到达目的位置仍是止步不前。当分度小到足以步量的时候,此时选择走直角或是斜线,在于每个人的选择,相信正常人不会选择在1平米的范围内选择走直角。所以真正的捷径在于方向的选择,这极大的缩短成功的路上所花费时间。孔子早在千年前,就用循环推广无限的方式,给出了现代数学微积分的理论思想,正所谓“学而不思则罔,思而不学则殆”,“思”便是人生的思考,方向的选择,“学”则是在成功之路上日夜积累的跬步。
推广
这篇关于量变与质变——“学而不思则罔,思而不学则殆”——圆锥世界的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!