本文主要是介绍精密单点定位(PPP)数据处理反演潮汐(四),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
前段时间,我又尝试用TerraPos处理一下SeaPath330的原始姿态和定位数据,看看反演潮位的效果如何。
首先,怎么预处理SeaPath330的定位和姿态数据,
记录格式如下1901200054.l09和1901200054.l10,咨询了SeaPath330的技术张工,对话如下:
张工,有个问题咨询一下,Seapath记录的RTCM数据格式.l09和IMU原始数据.l10怎么转成rinex和imu格式?
l10本身就是imu格式
l09 是rtcm,要轉成 rinex
rinex
直接改成imu可以吗?
對
l09改成rtcm?
L09 用这个转RInex
rinexconv.exe" -r 1 ***.rtcm > xxx.obs
-r 1 是第一个 天线 -r 2 是第二个
1是主天线吗?
就是位置天线?
對
朝船后的那个天线是天线1?
要查一下
船后的那个天线是天线1
张工,在处理惯导的数据的时候,出现这样的问题,
Initializing heading from velocity
No periods with suitable velocities found.
No periods with zero cross-track acceleration found.
张工,记录的gps和imu原始数据的位置是nrp(重心)?还是各自位置的?
各自的中心
heave值也是mru5处的?
對的
除了张工使用的命令程序以外,也可以用GUI方式转(推荐使用)
然后处理SeaPath的姿态和定位数据
选取当船在码头的时候,差分信号不好
采用TC模式,用10s 卡尔曼滤波,下图是高程曲线,效果有点惨不忍睹
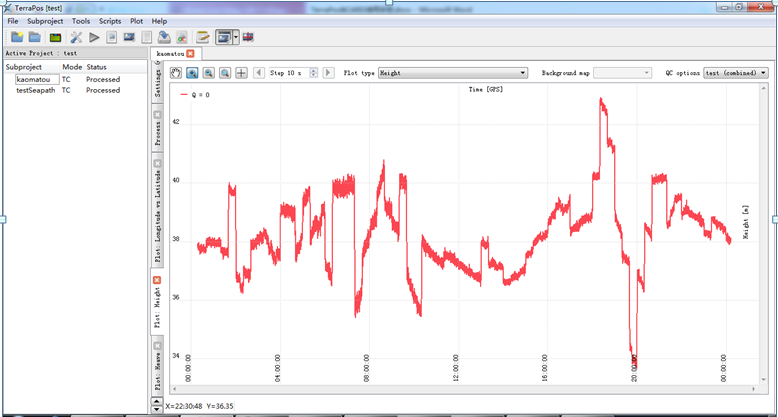
查看精度文件overall.txt,发现置信水平为95%时,高程误差为17.3cm,这个效果一般,没有达到10cm以内。
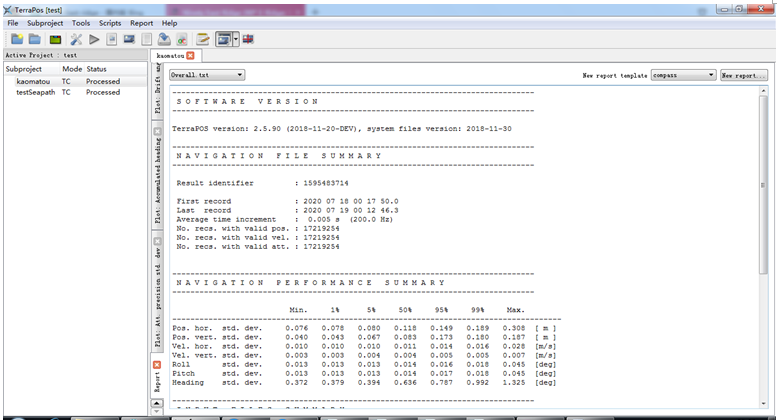
查看INS的精度评定文件,INS.txt
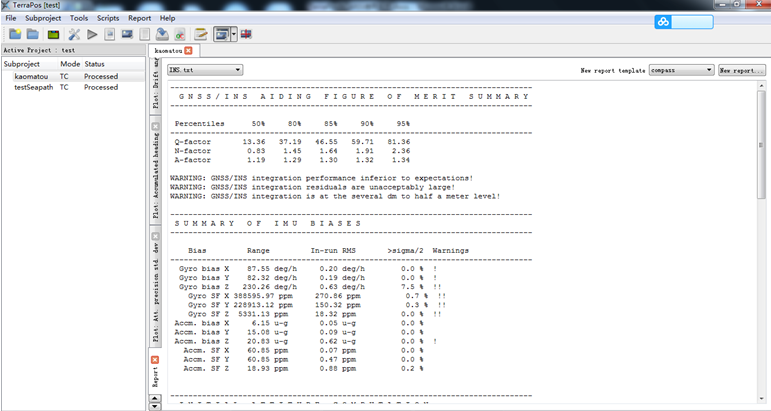
发现罗经误差较大,出现了报警信号,由于SeaPath采用双GPS的方式,如果在码头,航迹显示的是一个圆。
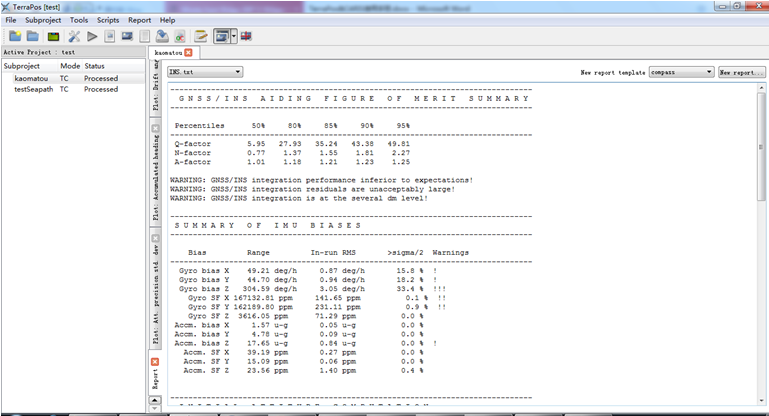
上面是采用10s滤波,效果较差,粗差有点多,下面采用1s的滤波
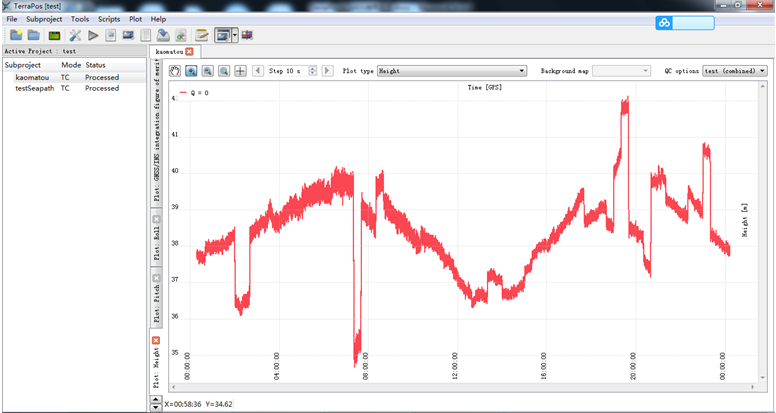
查看精度为overall.txt,发现置信水平为95%是,高程误差为19.9cm,虽然误差变化不大,但是高程曲线基本反映了潮位的起伏,但是有一些异常存在,至于这个异常存在,博主认为是卡尔曼滤波有些粗差仍然无法剔除,是不是需要人工剔除才可以?
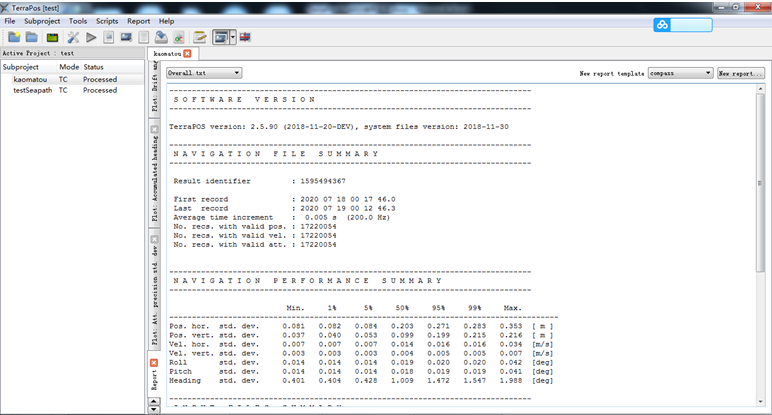
查看INS的精度评定文件,INS.txt
发现仍然是罗经报警
最后,我搜索了一下关于抗粗差的卡尔曼滤波的论文,有一篇文章魏世玉等《基于卡尔曼滤波的GNSS自动化监测数据粗差分析》
在GNSS( Global Navigation Satellite System) 自动化变形监测中,由于受观测条件的影响,如周跳、多路径效应以及接收机信号故障等,致使观测数据中难免包含粗差,极大降低了观测成果的准确性和可靠性。粗差的存在给后续变形分析和解释带来了困难,甚至得出错误结论。因此,粗差探测工作是自动化变形监测数据处理中的重要环节。
对于粗差探测,目前普遍采用以均值漂移模型为基础的粗差探测和以方差膨胀模型为基础的抗差估计等方法。这些方法具备严密的理论基础,当监测网图形强度较好且具备一定数量的多余观测时,上述方法均能很好地消除粗差对观测成果的影响。但在GNSS 自动化变形监测中,为了实时掌握变形体变形情况,通常需要提高监测频率,这就导致一次定位解算的观测时间变短,多余观测数也随之减少。这时按上
述方法很难对粗差进行准确的定位和剔除。
卡尔曼滤波是20 世纪60 年代初由卡尔曼等人提出的一种递推式滤波算法,其最大特点是能够剔除系统中的随机干扰,从而获得逼近真实情况的有用信息。如果将粗差看作GNSS 自动化监测中的随机干扰,便可利用卡尔曼滤波对其进行剔除,得到一组“干净”的观测值序列。因此,本文以GNSS 自动化平面位移监测数据为研究对象,利用卡尔曼滤波,建立监测点坐标序列粗差探测模型,对GNSS 自动化监测坐标序列粗差探测过程进行详细分析。最后通过实际监测数据分析,验证该模型的准确性和有效性。
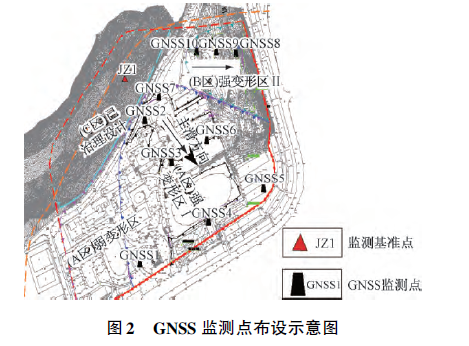
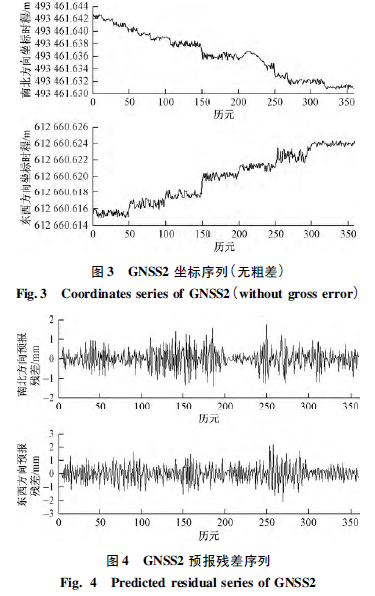
选取同一剖面监测点GNSS2 ( 位于主滑面坡顶)和GNSS4 ( 位于主滑面坡底) 连续1 个月( 2015 年5月) 的监测数据为分析对象,观测时段长为2 小时( 即连续观测2 小时的数据作为一次静态基线解算结果) ,共359 组有效坐标序列数据。
为分析滤波模型对粗差探测的敏感性,选取坡顶观测条件良好,且距基准站较近的GNSS2 在X 轴和Y轴方向的坐标序列( 图3) ,经分析发现,该序列无粗差情况。利用前5 个坐标分量序列分别进行二次拟合,以确定初始状态,从序列第6 个数据开始进行预报与滤波,得其在X 轴和Y 轴方向预报残差序列见图4。对上述无粗差坐标序列预报残差统计分析得X 方向预报残差中误差为0. 65 mm,Y 方向则为0. 82 mm。
由此可见,该滤波模型对粗差探测具有较高的灵敏性。
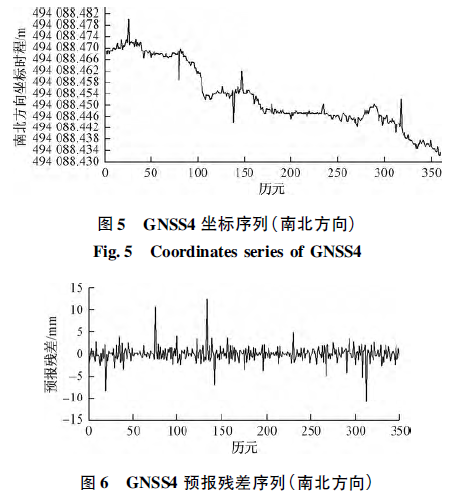
为验证模型探测粗差的有效性和准确性,选取坡底观测条件相对较差的GNSS4 在X 轴方向的坐标序列进行分析( 图5) 。该月监测期间,GNSS4 监测点上接收机存在蓄电池无法供电的情况,导致某些观测时段观测值数量不足,另外该监测点位于斜坡底部,卫星信号质量在某些时段可能会较差,因此解算出的坐标序列中极有可能存在粗差。利用前5 个无粗差坐标序列进行二次拟合,以确定滤波初始状态,并取3 倍拟合残差中误差作为粗差探测阈值( μ = 3. 5 mm,μ' = 4. 5mm) ,从序列第6 个数据开始进行预报与滤波,得其在X 轴方向预报残差序列见图6。
5 结语
本文将卡尔曼滤波应用于GNSS 自动化监测粗差探测,通过理论分析和实际监测数据验证,得出以下几点结论:
( 1) 卡尔曼滤波是一种对动态系统进行实时状态估计的有效方法,系统数学模型和噪声统计模型的合理建立是系统准确状态估计的关键。
( 2) 实验分析表明,在启动卡尔曼滤波之前,较为准确地确定初始状态及其方差阵D有利于滤波的快速稳定; 动态噪声和观测噪声的不合理选取将导致滤波发散。
( 3) 变形监测数据粗差探测的关键在于如何区分粗差与变形。本文利用粗差仅在某一时刻具有突变特征而变形往往伴随后续数据整体发生偏移,有效地剔除了GNSS 坐标序列中粗差。
是否可以这样,将GNSS的粗差剔除以后,再重新写成rinex格式,作为TerraPos的定位数据
这篇关于精密单点定位(PPP)数据处理反演潮汐(四)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





